Lesz-e olyan pillanat, amikor minden táncos ,,halott''?
Bevezetés
A Véletlen című modern ismeretterjesztő táncjátékban - amelyet a KöMaL Ifjúsági Ankétjának résztvevői is megtekinthettek az utolsó estén (december 22-én) - került elő a következő probléma:
Valaki feldob egy szabályos dobókockát 40-szer. Mindig feljegyzi, hogy melyik szám jött ki. Annak az eseménynek a valószínűségére vagyunk kíváncsiak, amelyben mind a hat szám éppen páratlan sokszor fordul elő.
Ez a kísérlet a darabban le is játszódott; mindegyik táncosnak volt egy sorszáma (éppen hatan voltak), s akinek a száma kijött, az vagy ,,meghalt'', ha addig táncolt, vagy ,,feltámadt'', ha addig a színpadon feküdt. A kérdés az volt, hogy lesz-e olyan pillanat, amikor mindenki a színpadon fekszik, feltéve, hogy kezdetben mindenki táncolt. Csak az érdekesség kedvéért jegyzem meg, hogy a premier és az utána következő két előadás alatt ez összesen egyszer következett be. Mint látni fogjuk, az esély kb. 0,36, tehát ez meglepően jó egyezés.
Honnan hová?
Legelőször tisztázzuk, mi is a kérdés. Minden dobásnál meg lehet mondani, hogy addig hány szám fordult elő páratlan sokszor. Kezdetben ez a szám 0, hiszen minden 0-szor fordult elő, és a nulla páros szám. Az első dobás után biztosan egy szám lesz, ami páratlan sokszor fordult elő, a többi páros. A második dobás után vagy újra az elsőt dobom, ekkor megint mind páros, tehát a páratlanok száma 0; vagy egy másikat dobok, akkor már két páratlan lesz. Hasonlóképpen lehet folytatni. Látható, hogy a páratlan sokszor előfordult értékek száma szerint 7 különböző állapot van: 0,1,2,3,4,5,6. Az első állapotból indulunk, és az utolsó állapotba kerülés esélye érdekel bennünket. Azt kell meghatározni, hogy az egyes állapotokból milyen állapotokba lehet átkerülni, s ezek az átmenetek milyen eséllyel következnek be.
Minden állapotból kétféleképpen léphetünk tovább: vagy 1-gyel nő, vagy 1-gyel csökken a páratlanok száma. Ilyenkor az állapotok közötti átmeneteket egy gráffal szokás szemléltetni. Esetünkben a gráf a következőképpen néz ki:
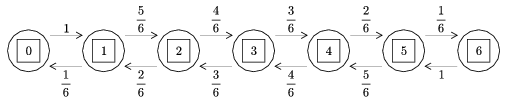
Az átmenetek valószínűségét is könnyű megadni: a 0-ból csak az 1-be lehet lépni, 1 eséllyel. Az 1-ből \(\displaystyle \frac{1}{6}\) eséllyel visszalépek a 0-ba, ha éppen azt az egy számot dobom, ami eddig egyedül páratlan sokszor fordult elő; \(\displaystyle \frac{5}{6}\) eséllyel másik számot dobok, és a ,,2 páratlan'' állapotba kerülök. Innen \(\displaystyle \frac{2}{6}\) eséllyel jutok vissza az 1 állapotba (az eddig páratlan sokszor előforduló két szám valamelyikét dobva), míg \(\displaystyle \frac{4}{6}\) eséllyel a 3-ba kerülök. Könnyen látszik, hogy innen \(\displaystyle \frac{3}{6}\) a visszajutás esélye a 2-be, és hasonlóan \(\displaystyle \frac{3}{6}\) a 4-be kerülésé. A továbbiakat az ábrán látjuk. A 6-ból 1 eséllyel kerülök vissza az 5-be. Mivel azonban a 6-ba kerülés esélye a kérdés, azért módosítsunk a szabályokon úgy, hogy innen már nem lehet kilépni, azaz 1 eséllyel itt maradok. Ekkor a kérdés az, hogy milyen eséllyel kerülök a 40 lépés során a 6-os állapotba. (Az most nem számít, hogy hányadik lépésben értem el a 6 állapotot, onnantól ott maradok. A táncjátékban ez nem így volt, ott tovább ment a dobálás, és újra vissza lehetett kerülni az 5 állapotba, stb.)
Nézzük meg, hogy két lépés után mi történik. Ekkor a 0, 2 állapotok egyikében lehetek csak. Milyen esélyekkel, ez a kérdés. Ezeket az esélyeket nyilván úgy lehet számolni, hogy a különböző lehetséges utak esélyeit összeadom. Gráfunk nagyon egyszerű, ezért nincs túl sok út az egyes átmenetekre: pl. a 2 pontból csak a 0-ba, vagy a 4-be juthatok, vagy visszakerülök a 2-be. Ez utóbbi két úton lehetséges: a 2-1-2 vagy a 2-3-2 módon. A függetlenség miatt a két esetnél két esély szorzata lép fel, és ezek összege lesz a helyben maradás esélye a 2 állapotban.
Vezessük be a következő jelöléseket. Jelölje \(\displaystyle p_k^{(\ell)}\) annak a valószínűségét, hogy \(\displaystyle \ell\) dobás után pontosan k darab szám fordult elő páratlan sokszor. Így az \(\displaystyle \ell\) dobás utáni helyzetet a
\(\displaystyle p_{0}^{(\ell)},p_{1}^{(\ell)},\dots,p_{6}^{(\ell)} \)
sorozat (más szóval eloszlás) írja le. A kezdeti (\(\displaystyle \ell\)=0-hoz tartozó) eloszlás nyilván 1,0,0,0,0,0,0, hiszen kezdetben 1 valószínűséggel - sőt biztosan - minden szám nullaszor, tehát páros sokszor fordult elő, vagyis 1 a valószínűsége annak, hogy 0 darab szám fordult elő páratlan sokszor, ezért 0 valószínűségű minden olyan esemény, amikor a páratlan sokszor előfordultak száma k \(\displaystyle \ge\)1.
Ha ismerem a kezdeti eloszlást, azaz hogy milyen eséllyel indulok az egyes pontokból, akkor az egy lépéssel későbbi eloszlást az átmenet valószínűségek segítségével lehet megkapni. Ha ugyanis az i-edik állapotból a j-edikbe való átmenet esélye a pij szám, akkor a teljes valószínűség tétele szerint a kezdeti p0(0), p1(0), ..., p6(0) eloszlásból a p0(1), p1(1), ..., p6(1) eloszlás lesz, ahol
\(\displaystyle p_{i}^{(1)}=\sum_{j=0}^{6}p_{j}^{(0)}\cdot p_{ji}\), és általában \(\displaystyle p_{i}^{(\ell+1)}=\sum_{j=0}^{6}p_{j}^{(\ell)}\cdot p_{ji}\).
Mátrixok
Az eloszlásokra kapott képletek sokkal áttekinthetőbbé és kezelhetőbbé válnak, ha a mátrixok nyelvére fordítjuk le őket.
Mátrixnak a számok téglalap-szerű, azaz (,,vízszintes'') sorokba és (,,függőleges'') oszlopokba rendezett táblázatát nevezzük. Például az
\(\displaystyle M=\left[\matrix{2&4&3\cr5&3&1\cr }\right] \)
mátrixnak két sora és három oszlopa van (ezt úgy is szokás mondani, hogy az M 2 x3-as mátrix). A 2,4,3,5,3,1 számok a mátrix elemei. Például a 3 az M első sorának harmadik eleme - rövidebben az M (1,3)-adik eleme, ami esetünkben egyenlő az M (2,2)-edik elemével. Egy mátrix állhat akár egyetlen sorból vagy egyetlen oszlopból is, ilyenkor sormátrixról, ill. oszlopmátrixról beszélünk; így egy tetszőleges mátrix sorai és oszlopai maguk is mátrixok.
Mátrixokkal többféle művelet is értelmezhető; ezúttal csak egyikükkel foglalkozunk, a mátrixok szorzásával. Először egy
\(\displaystyle \underline{a}=\left[\matrix{a_1&a_2&\ldots&a_n}\right] \)
sormátrixnak egy
\(\displaystyle \underline{b}=\left[\matrix{b_1\cr b_2\cr \vdots\cr b_n}\right] \)
oszlopmátrixszal való szorzatát definiáljuk: legyen a .b az az 1 x1-es mátrix - vagyis egy szám -, amelynek egyetlen eleme a1b1 + a2b2 +...+ anbn. Két mátrix szorzatát ezután a következőképpen értelmezzük. Legyen A n xk-as, B pedig kxr-es mátrix (azaz megköveteljük, hogy A sorai ugyanolyan hosszúak legyenek, mint B oszlopai); ekkor AB az az n xr-es mátrix, amelynek (i,j)-edik eleme az A i-edik sorának a B j-edik oszlopával való szorzatának egyetlen eleme (1 \(\displaystyle \le\)i \(\displaystyle \le\)n, 1 \(\displaystyle \le\)j \(\displaystyle \le\)r). Például
\(\displaystyle \left[\matrix{2&4&3\cr5&3&1\cr }\right]\cdot\left[\matrix{1&0\cr0&2\cr 3&5}\right]= \left[\matrix{11&23\cr8&11\cr}\right]. \)
Feltűnő, hogy általában két különböző alakú mátrixot szorzunk egymással, és a szorzat alakja általában különbözik mind a két tényezőnek az alakjától. Ennek láttán talán nem annyira meglepő, hogy ez a szorzási művelet nem kommutatív: ha értelmezett az AB szorzat, akkor a BA szorzat rendszerint nem is értelmezett; de ha mégis, az alakja rendszerint eltér AB alakjától. Kivétel, ha A és B egyaránt n xn-es mátrixok; ekkor AB és BA is értelmezett, és mindketten n xn-esek - de BA általában még ekkor is különbözik AB-től. Belátható viszont, hogy a mátrixszorzás asszociatív: ha A n xk-as, B k xr-es, C pedig r x\(\displaystyle \ell\)-es mátrix, akkor (A .B).C = A.(B .C). Ezért többtényezős szorzatokban a zárójeleket elhagyhatjuk (ugyanezt tesszük többnyire a szorzás jelével is).
Markov-láncok
A mátrixokkal történt bevezető ismerkedés után térjünk vissza a 2. rész végén kapott
\(\displaystyle p_{i}^{(\ell+1)}=\sum_{j=0}^{6}{p_{j}^{(\ell)}\cdot p_{ji}.} \)
képlethez. Jelölje M azt a 7 x7-es mátrixot, amelynek (i,j)-edik eleme pi-1,j-1, vagyis annak a valószínűsége, hogy az i-1 állapotból egy dobással a j-1 állapotba kerülünk:
\(\displaystyle \left[\matrix{ 0&1&0&0&0&0&0\cr\frac{1}{6}&0&\frac{5}{6}&0&0&0&0\cr 0&\frac{2}{6}&0&\frac{4}{6}&0&0&0\cr 0&0&\frac{3}{6}&0&\frac{3}{6}&0&0\cr 0&0&0&\frac{4}{6}&0&\frac{2}{6}&0\cr 0&0&0&0&\frac{5}{6}&0&\frac{1}{6}\cr 0&0&0&0&0&1&\fbox{0} }\;\right]\), illetve a módosítással \(\displaystyle \left[\matrix{ 0&1&0&0&0&0&0\cr \frac{1}{6}&0&\frac{5}{6}&0&0&0&0\cr 0&\frac{2}{6}&0&\frac{4}{6}&0&0&0\cr 0&0&\frac{3}{6}&0&\frac{3}{6}&0&0\cr 0&0&0&\frac{4}{6}&0&\frac{2}{6}&0\cr 0&0&0&0&\frac{5}{6}&0&\frac{1}{6}\cr 0&0&0&0&0&0&\fbox{1} }\;\right]\),
ami úgy adódott, hogy a hetedik állapot ún. nyelő lett, onnan (1 valószínűséggel) nem lehet kilépni.
Jelölje \(\displaystyle \mathbf{p}^{(\ell)}\) az \(\displaystyle \ell\)-edik eloszlást leíró \(\displaystyle \left[\matrix{p_0^{(\ell)}&p_1^{(\ell)}&\dots&p_6^{(\ell)} }\right]\) sormátrixot; ekkor (minden \(\displaystyle \ell\)-re) az (1) képlet a mátrixszorzás nyelvén a következőt jelenti:
\(\displaystyle \mathbf{p}^{(\ell+1)}=\mathbf{p}^{(\ell)}\cdot M \)
Alkalmazzuk ezt rendre \(\displaystyle \ell\)= 0,1,2,3, ...-ra:
p(1) = p(0) .M, p(2)= p(1) .M = (p(0) .M).M = p(0) .M2,
p(3) = (p(0) .M2) .M =p(0) .M3, p(4) =(p(0) .M3).M =p(0) .M4,
ahonnan látható - és egyszerű indukcióval igazolható -, hogy
\(\displaystyle \mathbf{p}^{(\ell)}=\mathbf{p}^{(0)}\cdot M^{\ell}=\left[\matrix{ 1&0&0&0&0&0&0}\right]\cdot M^{\ell}; \)
ez éppen az M mátrix \(\displaystyle \ell\)-edik hatványának az első sora.
Eredeti feladatunkra visszatérve, a ,,minden táncos halott'' esemény 40 lépésen belüli bekövetkezésének valószínűségét az M mátrix 40-edik hatványában az első sor utolsó eleme adja meg. Egy mátrix negyvenedik hatványát kézzel kiszámolni elég nehézkes, ezért használjunk gépet (már egy grafikus kalkulátor is megteszi); a keresett negyvenedik hatvány:
\(\displaystyle \mathbf{P}^{40}=\left[\matrix{ 0{,}022&0&0{,}321&0&0{,}294&0&\fbox{0{,}363}\cr 0&0{,}129&0&0{,}41&0&0{,}098&0{,}363\cr 0{,}0214&0&0{,}311&0&0{,}285&0&0{,}382\cr 0&0{,}123&0&0{,}391&0&0{,}094&0{,}393\cr 0{,}0196&0&0{,}285&0&0{,}262&0&0{,}433\cr 0&0{,}098&0&0{,}312&0&0{,}075&0{,}515\cr 0&0&0&0&0&0&1 }\;\right]. \)
A minket érdeklő szám az első sor hetedik eleme, amelyre gépi kerekítésekkel 0,363 adódik: kicsit több, mint \(\displaystyle \frac{1}{3}\) annak az esélye, hogy a 40 dobás során előáll az az állapot, hogy minden táncos ,,halott''.
A számolást kissé egyszerűsítheti a következő észrevétel: mivel a 0-ból indulunk, azért a negyvenedik lépésben csak páros pontban lehetünk, így elég a kétlépéses folyamatot 20-szor ismételni. Ekkor 7x7-es helyett csak 4 x4-es a hatványozandó mátrix. Rajzoljuk fel, hogy két lépés egymásutánjának eredményeként mi történhet:
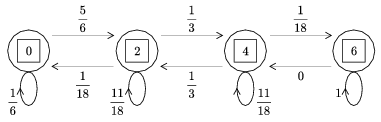
Itt csak négy állapot lehet, az átmenet valószínűségek mátrixát úgy kapjuk, hogy az eredeti ábrán két lépést összevonunk. Így viszont egy (dupla) lépés eredményeként pozitív valószínűséggel helyben is maradhatunk, ezt jelzik az ábrán levő hurkok; pl. a 0 állapot esetén a helyben maradás valószínűsége \(\displaystyle 1\cdot\frac{1}{6}\), a 2 esetén: \(\displaystyle \frac{2}{6}\cdot\frac{5}{6}+ \frac{4}{6}\cdot\frac{3}{6}=\frac{22}{36}=\frac{11}{18}\). Mindezek az eredeti ábra két lépéses valószínűségeiből adódnak. Ezzel a mátrix:
\(\displaystyle Q=\left[\matrix{ \frac{1}{6}&\frac{5}{6}&0&0\cr \frac{1}{18}&\frac{11}{18}&\frac{1}{3}&0\cr 0&\frac{1}{3}&\frac{11}{18}&\frac{1}{18}\cr 0&0&0&1}\right]. \)
Eszerint a feladatunk e 4 x4-es mátrix 20-adik hatványának a kiszámítása; az eredmény a következő:
\(\displaystyle Q^{20}=\left[\matrix{ 0{,}0221&0{,}3206&0{,}2942&\fbox{0{,}3631}\cr 0{,}0213&0{,}3108&0{,}2852&0{,}3827\cr 0{,}0196&0{,}2852&0{,}2616&0{,}4335\cr 0&0&0&1\cr }\;\right]. \)
Az eredmény számunkra érdekes része természetesen ugyanaz, mint az előbb (csak itt nagyobb pontossággal számoltunk, egy tizedes jeggyel tovább menve az eredeti mátrixnál is 0,3631 lett volna az eredmény).
Természetesen vetődik fel a kérdés: mennyire (ill. hogyan) függ a kapott eredmény a dobások számától. A 6-os állapot előfordulásának valószínűsége nyilván monoton növő függvénye a dobások számának. Az viszont talán meglepő, hogy tetszőlegesen sok dobást megengedve a valószínűség akármilyen közel kerülhet az 1-hez. A mátrixok nyelvén ez úgy is fogalmazható, hogy az M mátrix n-edik hatványában az első sor utolsó eleme tart az 1-hez, ha n tart a végtelenhez. (Ahhoz azonban, hogy közel legyünk az 1 valószínűséghez nagyon sok dobás kell, pl. 200 dobás esetén még mindig ,,csak'' 0,994 a keresett esély.) Mindez annak a következménye, hogy a rendszerünk nyelő. Sőt, a 6-os állapot bekövetkezésének valószínűsége akkor is 1-hez tart, ha nem az \(\displaystyle \left[\matrix{1&0&0&0&0&0&0\cr }\right]\) eloszlásból indulunk ki.
Még érdekesebb a helyzet akkor, ha az átmenet valószínűségek mátrixa olyan, hogy valamelyik hatványának minden eleme pozitív (az ilyet reguláris átmenet mátrixnak nevezzük). Ekkor egyrészt az eloszlásoknak létezik (ugyancsak a kiindulótól független) ,,határértéke'' - azaz nem csak az egyik állapot elérésének a valószínűsége konvergál, hanem valamennyié. Sőt, ilyenkor az átmenet valószínűségek mátrixának a hatványai is egy bizonyos mátrixhoz tartanak (a megfelelő helyen álló elemek sorozata konvergens). Megjegyzendő, hogy ez az utóbbi tény az ,,erősebb'' tulajdonság, amiből az előbbi (az eloszlások sorozatának konvergenciája) viszonylag egyszerűen következik. Nyelő folyamatot leíró mátrix azonban soha nem reguláris - ezt az Olvasó könnyűszerrel beláthatja.
Az olyan folyamatokat, ahol egy adott állapotba kerülés esélye az előző állapotnak és az átmeneti valószínűségek mátrixának szorzatából kapható meg, Markov orosz matematikus után szokás Markov-láncnak nevezni. Markov foglalkozott először szisztematikusan az ilyen problémákkal, ő volt az egyik megalapítója a híres orosz valószínűségszámítási iskolának, amelynek legismertebb alakjai még a XIX. században Csebisev és a XX. században Kolmogorov voltak. Nagyon sok folyamatot lehet ezzel a modellel leírni; az érdeklődőknek a következő magyar nyelvű olvasmányt ajánljuk a témához: J. G. Kemeny - J. L. Snell - G. L. Thompson: A modern matematika alapjai, Műszaki Könyvkiadó, 1971. (Témánk a 291-312. oldalakon található, érdekes alkalmazásai pedig a 440-477. oldalakon olvashatók.)
Vancsó Ödön

