Püthagorasz óta ismeretes, hogy "a" és "b" természetes számok barátságos számpárt alkotnak, ha "a" önmagától különböző osztóinak összege "b", és "b" önmagától különböző osztóinak összege "a". A barátságos számpár tagjai közül az egyik értelemszerűen osztódús (kövér szedés), a másik osztószegény. Ezek a párok a következők:

(220,284), (1184,1210), (2620,2924), (5020,5564), (6232,6368), (10744,10856), ...

Nyitott kérdés, hogy a számuk véges vagy végtelen. Erdős Pál feltételezése szerint végtelen.

Ha "a" és "b" valódi osztóit tekintjük, és igaz, hogy "a" valódi osztóinak összege "b", és "b" valódi osztóinak összege "a", akkor "a" és "b" valódi barátságos számpárt alkotnak. Ezek a következők:

(48;75), (140;195), (1575;1648), (1050;1925), (2024;2295), (8892;16587), (5775;6128), (9504;20735), ..., (1236536;1459143),...

Barátságos láncról beszélünk, ha egy tetszőleges összetett számból kiindulva képezzük az önmagától különböző osztóinak összegét, majd az így keletkezett szám önmagától különböző osztóinak összegét és így tovább. Mivel az összetett számok száma végtelen és bármelyikből kiindulhatunk, végtelen sok barátságos lánc van. Egy ilyen lánc például:

24, 36, 56, 64, 63, 41

Kérdés, hogy létezik-e végtelen hosszú lánc. A válasz jelenleg ismeretlen. A véges láncok háromfélék lehetnek: vagy prímben vagy tökéletes számban vagy hurokban végződnek.

Prímben végződő barátságos láncok például:

(a) 20, 22, 14, 10, 8, 7

(b) 48, 76, 64, 63, 41

(c) 52, 46, 26, 16, 15, 9, 4, 3

(d) 68, 58, 32, 31

(e) 172, 136, 134, 70, 74, 40, 50, 43

(f) 174, 186, 198, 270, 450, 659

(g) 244, 190, 170, 154, 134, 70, 74, 40, 50, 43

(h) 250, 218, 112, 136, 134, 70, 74, 40, 50, 43

(i) 450, 759, 393, 135, 105, 87, 33, 15, 9, 4, 3

A lánc lehet növekvő (f), csökkenő (c,d) vagy ingadozó (a,b,e,g,h,i).

A növekvő lánc elemei - az utolsó kivételével - osztódúsak. A prímszámban végződő csökkenő lánc elemei osztószegények.

A 43 prímszámban végzodo barátságos láncok struktúrájának egy részlete:

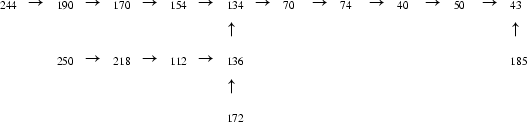
A tökéletes számban végződő barátságos lánc abban különbözik az előzőtől, hogy a láncvég nem prímszám, hanem egy tökéletes szám. Ilyen láncok például:

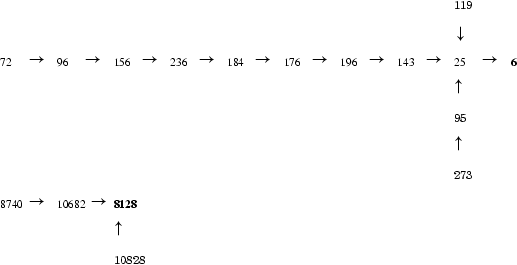
Barátságos számpárban végződő lánc esetén a láncvég a barátságos számpárok valamelyike.

Néhány példa ilyen láncokra:

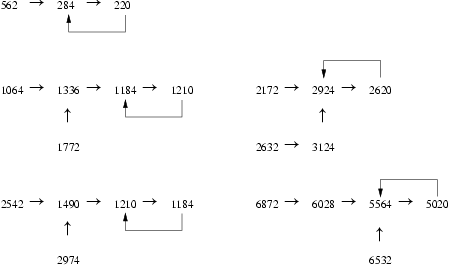
Prímben végződő barátságos valódi lánc adódik, ha egy tetszőleges összetett számra képezzük valódi osztóinak összegét, az így nyert számmal ugyanígy járunk el és így tovább. Ilyen láncok például:

117, 64, 62, 33, 14, 9, 3

69, 26, 15, 8, 6, 5

38, 21, 10, 7

68, 57, 22, 13

...

A tökéletes számban végződő barátságos láncok lényegileg hurokban végződnek, mivel egy tökéletes szám önmagától különböző osztóinak összege maga a tökéletes szám, és így a folyamat vége egy egyelemű hurok. Hasonlóképpen egy barátságos számpárban végződő barátságos lánc egy kételemű hurokban végződik. Ebből adódik a következő kérdés. (2)

Léteznek-e tetszőleges elemszámú, hurokban végződő barátságos láncok, azaz létezik-e az a1, a2, a3, ... am hurok szerkezetű barátságos számhalmaz az alábbi értelemben?

Képezzük az a1 összetett szám önmagától különböző osztóinak összegét, így adódik a2 , mellyel ugyanígy járunk el, így kapjuk az a3 elemet és így tovább, végül am önmagától különböző osztóinak összege az a1 számot adja.

Az m=1 elemű, triviális hurok létezik, ez a tökéletes szám.

Az m=2 elemu hurkok is léteznek, ezek a barátságos számpárok.

Példa m=5 elemű hurokra:

Olyan barátságos láncok, melyek 4 elemu hurokban végződnek, pl. az alábbiak:

További 4 elemű hurkok:

Végül példát adunk 28 elemű barátságos hurokra:

Tehát a püthagoraszi gondolat általánosítása is igaz, léteznek a (2)-ben definiált hurok szerkezetű barátságos számhalmazok.

Irodalomjegyzék

Paul Hoffman: A PRÍMEMBER; Scolar, 1999

Oystein Ore: Bevezetés a számelmélet világába; Gondolat, 1977

Gyarmati E. - Turán P.: Számelmélet; ELTE Egyetemi jegyzet

Erdős P. - Surányi J.: Válogatott fejezetek a számelméletből; Tankönyvkiadó, Budapest, 1978

Sárközy A.: Számelmélet; Műszaki Könyvkiadó, Budapest, 1978

2000. dec. 20.