Beszámoló a 2011. évi Eötvös-versenyről

Radnai Gyula

2011. október 14-én délután 3 órai kezdettel került sor a háború utáni 63. Eötvös-versenyre Budapesten és a terv szerint 15, valójában csak 9 vidéki városban. Sajnos Sopronban nem sikerült megrendezni a versenyt, Békéscsabán, Egerben, Nyíregyházán, Székesfehérváron és Szombathelyen pedig egyetlen versenyző sem jelent meg a verseny meghirdetett helyszínén. Feltűnő volt a vidéki diákok érdektelensége; még olyan egyetemi városban is, mint Debrecen, csupán egyetlen versenyző akadt. Az Eötvös-verseny rendezője az Eötvös Loránd Fizikai Társulat, amelynek helyi csoportjai adják a verseny helyi szervezőit. Az ő munkájuk veszett kárba az említett városokban. Szegeden és Pécsett 11-11 versenyző, Budapesten 67 versenyző indult, a többi helyszínen egyaránt 10-nél kevesebben voltak. Először fordult elő, hogy a vidéki helyszíneken együttvéve kevesebb versenyző (41) jelent meg, mint Budapesten.

Az összesen 108 versenyzőből 26-an voltak a két nagy budapesti egyetem (BME, ELTE) elsőéves hallgatói, és pontosan ugyanennyi diák jött a Fővárosi Fazekas Mihály Gyakorló Gimnáziumból. Az egyetemisták közül öten érettségiztek a Fazekasban, négyen az ELTE Apáczai Csere János Gyakorló Gimnáziumban. Innen további hat diák indult a versenyen. A vidéki középiskolák közül a szegedi Radnóti Miklós Kísérleti Gimnáziumból jött a legtöbb (8) versenyző. Külföldi versenyző egyetlen akadt, az ELTE egyik elsőéves hallgatója.

A feladatokat az Eötvös-versenybizottság tűzte ki, és a versenyzők dolgozatait is ugyanez a bizottság értékelte. (Tagjai Honyek Gyula, Károlyházy Frigyes, Vigh Máté, elnöke Radnai Gyula.) A feladatok megoldására 300 perc állt rendelkezésre.

Ismertetjük a feladatokat és azok megoldását.

1. feladat. Pályafutásuk végén a sorsukra hagyott műholdak a sebesség négyzetével arányos légellenállási erő hatására fokozatosan veszítenek mechanikai energiájukból, és végül a légkör sűrűbb rétegeibe érve elégnek. Belátható, hogy az eredetileg körpályákon keringő műholdak a Föld felszínéhez közeledve mindvégig közelítőleg körpályákon haladnak, miközben a ,,körpályák'' sugara lassan csökken.

Tegyük fel, hogy egy m=500 kg tömegű műholdat, amely az Egyenlítő síkjában, h=400 km -es magasságban körpályán kering, magára hagynak! A műholdra ható légellenállási erőt az F_lég=K\(\displaystyle \varrho\)v² alakban adhatjuk meg, ahol K=0,23 m², \(\displaystyle \varrho\) a levegő sűrűsége a műhold magasságában, v pedig a műhold sebessége.

a) Határozzuk meg a műhold áltozását, miközben pályamagassága a felére csökken (h \(\displaystyle \rightarrow\)h/2)!

b) A légellenállási erő, valamint a műholdra ható két erő (gravitációs és légellenállási) eredőjének pályamenti (érintőleges) összetevője között egy egyszerű összefüggés állapítható meg. Hogy szól ez?

c) Mekkora a levegő sűrűsége h/2=200 km magasságban, ha itt egy fordulat alatt a műhold pályasugara 100 m-rel csökken?

A megoldáshoz szükséges további adatokat táblázatokból vehetjük.

(Honyek Gyula)

Megoldás. Adottak:

m=500 kg, h=400 km=4^.10⁵ m,

\(\displaystyle r_{1}=R+h,\quad r_{2}=R+\frac{h}{2},\)

\(\displaystyle F_\text{lég}=K\varrho v^2~(\text{ahol}~K=0{,}23~{\rm m}^2),\quad\Delta r=-\varepsilon\ (=-100~\rm m).\)

Táblázatból vehető a Föld egyenlítői R sugara, M tömege és a gravitációs törvényben szereplő \(\displaystyle \gamma\) állandó:

R=6378 km=6,378^.10⁶ m,

M=5,974^.10²⁴ kg,

\(\displaystyle \gamma\)=6,673^.10^-11 m³/(kg^.s²).

a) A feladatban megfogalmazott feltételek szerint ,,a műholdak a Föld felszínéhez közeledve mindvégig közelítően körpályán haladnak'', ezért jó közelítésben írhatjuk:

\(\displaystyle F_{\rm grav}=ma_{\rm cp},\qquad\gamma\frac{mM}{r^2}=m\frac{v^2}{r}. \)

Ennek alapján

\(\displaystyle v=\sqrt{\frac{\gamma M}{r}}, \)

amelybe behelyettesítve r₁ és r₂ értékeit, megkapjuk a két sebességet:

\(\displaystyle v_{1}=7669{,}0~\frac{\rm m}{\rm s},\qquad v_{2}=7784{,}7~\frac{\rm m}{\rm s}. \)

A műhold sebességváltozása tehát

\(\displaystyle {v_{2}-v_{1}=115{,}7~\frac{\rm m}{\rm s}}\)>0.

A légellenállás következtében nőtt a műhold sebessége! Szokás ezt űrhajózási paradoxonnak is nevezni. A légellenállási, súrlódási erő munkája szükségképpen negatív, mégis nő a műhold mozgási energiája! Hogyan lehetséges ez? Erre kaphatunk választ a feladat b) és c) részének megoldása során. Érdemes lesz mindkét esetben abból indulunk ki, hogyan változik meg a műhold mechanikai összenergiája, vagyis a kinetikus és potenciális energia összege. Ez az, ami a légellenállási erő hatására csökkenhet.

b) A légellenállási erő teljesítménye:

\(\displaystyle \overrightarrow{F}_\text{lég}\cdot\overrightarrow{v}=-{F}_\text{lég}\cdot{v}<0. \)

Ez egyenlő az összenergia változási sebességével:

Az összenergia kinetikus és potenciális részből áll:

\(\displaystyle E_\text{össz}=E_\text{kin}+E_\text{pot} =\frac12mv^2+\left(-\gamma\frac{mM}{r}\right). \)

E két rész azonban kifejezhető egymásból. Írjuk fel újra a dinamika alaptörvényét:

\(\displaystyle \gamma\frac{mM}{r^2}=m\frac{v^2}{r},\qquad\text{azaz}\qquad\gamma\frac{mM}{r}=m{v^2}, \)

amiből kapjuk:

\(\displaystyle E_\text{kin}=\frac12\,mv^2=\frac12\,\gamma\frac{mM}{r}=\frac12(-E_\text{pot}). \)

Az összenergiát tehát így is felírhatjuk:

\(\displaystyle E_\text{össz}=E_\text{kin}+E_\text{pot}=E_\text{kin}-2E_\text{kin}=-E_\text{kin}<0. \)

(Az, hogy az összenergia negatív, nem kell, hogy megijesszen senkit, az atomfizikában számos példát látunk erre.)

Most tehát (1) így írható:

\(\displaystyle -{F}_\text{lég}\cdot{v}=-\frac{\Delta E_\text{kin}}{\Delta t}, \)

illetve

\(\displaystyle {F}_\text{lég}\cdot{v}=\frac{\Delta\left(\frac12mv^2\right)}{\Delta t}= mv\frac{\Delta v}{\Delta t}=mv\,a_{\rm t}. \)

A légellenállásra egy érdekes kifejezést kaptunk:

Az ma_t kifejezés a tangenciális (pályamenti) eredő erőt adja, amely most a gravitációs erő pályamenti összetevőjének és a légellenállási erőnek az eredője (1. ábra), tehát

\(\displaystyle ma_{\rm t}={F}_{\text{grav}\|}-{F}_\text{lég}. \)

Ezt vessük össze (2)-vel:

\(\displaystyle {F}_\text{lég}={F}_{\text{grav}\|}-{F}_\text{lég}. \)

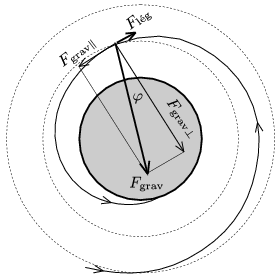
1. ábra. A feladat számadataival: \(\displaystyle {F}_\text{grav}=4{,}6~\)kN, \(\displaystyle {F}_\text{lég}=5{,}6~{\rm mN}\), \(\displaystyle \varphi\)=1,2^.10^-6 rad=0,25''. A vázlatos ábra nem méretarányos

Az az egyszerű összefüggés tehát, amely a légellenállási erő, valamint a műholdra ható két erő (gravitációs és légellenállási) eredőjének pályamenti összetevője között fennáll az, hogy e kettő nagysága egyenlő egymással.

c) Ismét az összenergia változásából érdemes kiindulnunk, de az összenergiát most ne a kinetikus, hanem a potenciális energiával fejezzük ki, felhasználva az \(\displaystyle E_\text{kin}=-E_\text{pot}/2\) összefüggést:

\(\displaystyle E_\text{össz}=E_\text{kin}+E_\text{pot} =-\frac{E_\text{pot}}{2}+E_\text{pot}=\frac{E_\text{pot}}{2}.\)

\(\displaystyle \frac{\Delta E_\text{össz}}{\Delta t}=\frac12\,\frac{\Delta E_\text{pot}}{\Delta t},\)

ami \(\displaystyle \Delta\)r-rel szorozva és osztva így is írható:

\(\displaystyle \frac{\Delta E_\text{össz}}{\Delta t}=\frac12\,\frac{\Delta E_\text{pot}}{\Delta r}\,\frac{\Delta r}{\Delta t}. \)

Mit mondhatunk a sugár változási sebességéről? Ismert adat, hogy egyetlen fordulat során a pályasugár \(\displaystyle \varepsilon\)=100 méterrel csökken, tehát

\(\displaystyle \frac{\Delta r}{\Delta t}=\frac{-\varepsilon}{T} =\frac{-\varepsilon}{\;\frac{2r\pi}{v}\;}. \)

Határozzuk meg a potenciális energia és a pályasugár változásának viszonyát:

\(\displaystyle \frac{\Delta E_\text{pot}}{\Delta r} =\frac{\Delta\left(-\gamma\frac{mM}{r}\right)}{\Delta r}=\gamma\frac{mM}{r^2}. \)

Most már felírhatjuk az (1) egyenletet, amelyben az összenergiát a potenciális energiával fejezzük ki:

\(\displaystyle -{F}_\text{lég}\cdot{v}=\frac{\Delta E_\text{össz}}{\Delta t}=\frac12\,\frac{\Delta E_\text{pot}}{\Delta t}=\frac12\,\frac{\Delta E_\text{pot}}{\Delta r}\,\frac{\Delta r}{\Delta t},\)

\(\displaystyle -{F}_\text{lég}\cdot{v}=\frac12\,\gamma\frac{mM}{r^2}\,\frac{-\varepsilon}{\;\frac{2r\pi}{v}\;},\)

\(\displaystyle {F}_\text{lég}=\frac{1}{4\pi}\,\gamma\frac{mM}{r^3}\,\varepsilon,\)

\(\displaystyle K\varrho v^2=\frac{1}{4\pi}\,\gamma\frac{mM}{r^3}\,\varepsilon.\)

Ebben az egyenletben már csak \(\displaystyle \varrho\) az egyetlen ismeretlen, éppen ezt kellett kiszámítanunk! De hogy még szebb, elegánsabb formulát kapjunk, használjuk fel újra a v²=\(\displaystyle \gamma\)M/r összefüggést, így a következőt kapjuk:

\(\displaystyle \varrho=\frac{1}{4\pi\,K}\,\frac{m}{r^2}\,\varepsilon. \)

r=r₂, valamint \(\displaystyle \varepsilon\) megadott értékét behelyettesítve

\(\displaystyle \varrho=4\cdot10^{-10}~\frac{\rm kg}{\rm m^3}. \)

Kiegészítés: Az a) kérdésre mg=mv²/r felhasználásával is válaszolhatunk, ha figyelembe vesszük a gravitációs gyorsulás magasságfüggését: \(\displaystyle g=g_{0}\left(1-\frac{h}{r}\right)^{2}\). Ezzel

\(\displaystyle v=\sqrt{gr}=\left(1-\frac{h}{r}\right)\,\sqrt{g_{0}r}, \)

ahol g₀ az egyenlítői gravitációs gyorsulás, amely azonban a táblázatban adott egyenlítői nehézségi gyorsulásnál nagyobb! A különbség a Föld forgásából adódó ,,centri'' gyorsulás.

2. feladat. Egy függőlegesen álló, henger alakú zárt tartály magassága legyen mondjuk 20 cm! Tegyük fel, hogy a tartály falának és belső tartalmának hőmérséklete huzamos ideje T=1 ^oC! A tartalom pedig egy, a tartály alaplapját borító papírvékonyságú vízréteg és fölötte ennek a telített gőze, más semmi. Az oldalfalat hőszigetelőnek tekinthetjük, az alap- és fedőlap azonban igen jó hővezető vékony fémlemez, amelyeknek a hőmérsékletét kívülről szabályozhatjuk.

A lehetőséggel élve emeljük a fedőlap hőmérsékletét T_f=100 ^oC-ra, miközben az alaplap hőmérsékletét T=1 ^oC-on tartjuk, és gondoskodjunk róla, hogy ezek az értékek elég sokáig így maradjanak! Várjuk meg, amíg az edényben kialakul a víz, illetve a gőz új stacionárius állapota, amely már nem változik tovább!

a) A korábbi egyensúlyi állapothoz képest megváltozott-e említésre méltó mértékben a gőzállapotban lévő vízmolekulák száma, és ha igen, akkor nőtt vagy csökkent?

b) Vajon mi lenne a válasz, ha a kezdeti állapotban a vízréteg magassága 10 cm lenne?

(Károlyházy Frigyes)

Megoldás. Ha egy folyadék saját telített gőzével érintkezik, akkor a gőz nyomása csak közös hőmérsékletüktől függ. Az alul levő 1 ^oC-os víz felett a gőz nyomása tehát mindkét esetben ugyanannyi. (A táblázatból interpolációval leolvasható ennek aktuális értéke: 660 Pa.)

A gőznyomás az egész edényben ugyanakkora, de abban az esetben, ha a hőmérséklet felfelé emelkedik, a gőz sűrűsége felfelé csökken. (Szintén a táblázatból olvasható ki, hogy az 1 ^oC-os telített gőz sűrűsége 5,2 g/m³, amiből egy átlagosan 50,5 ^oC-os gőz sűrűségére ,,ideális gáz közelítésben'' 4,4 g/m³ adódik.)

A gőz új stacionárius (időben állandó) állapotában tehát a gőz átlagos sűrűsége kisebb lett, vagyis a gőzállapotban levő vízmolekulák száma csökkent (2. ábra)!

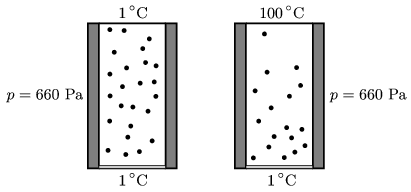
2. ábra

b) Ha a vízréteg magassága kezdetben 10 cm, a víz kitölti az edény felét. Felette azonban ugyanúgy 1 ^oC hőmérsékletű és 660 Pa nyomású telített gőz van, mint az a) esetben.

Amikor viszont a fedőlap hőmérsékletét 100 ^oC-ra emeljük, már nem mondhatjuk, hogy az egész víz 1 ^oC-os marad, ugyanúgy, mint amikor ,,papírvékonyságú'' volt. Azt se állíthatjuk persze, hogy jelentősen felmelegszik a víz felső rétege, mivel a víz sokkal jobb hővezető, mint a vízgőz. Mennyire melegszik hát fel?

Táblázatból kiolvasható, hogy a vízgőz hővezetési együtthatója

\(\displaystyle \lambda_\text{gőz}=18{,}0\cdot10^{-3}\,\frac{\rm J}{\rm m\;K\;s}, \)

míg a víz hővezetési együtthatója

\(\displaystyle \lambda_\text{víz}=0{,}587\,\frac{\rm J}{\rm m\;K\;s}= 587\cdot10^{-3}\,\frac{\rm J}{\rm m\;K\;s}. \)

Mivel a vízréteg és felette a vízgőz ugyanolyan (10 cm) magas, és a kialakuló hőmérsékletkülönbségek fordítva arányosak a hővezetési együtthatókkal, ezért a víz tetejének és a vele érintkező vízgőznek a közös hőmérsékletét T_k-val jelölve felírhatjuk:

\(\displaystyle \frac{T_{\rm k}-1~{}^\circ{\rm C}}{100~{}^\circ{\rm C}-T_{\rm k}} =\frac{\lambda_\text{gőz}}{\lambda_\text{víz}}=\frac{18\cdot10^{-3}}{587\cdot10^{-3}}. \)

Ennek alapján kapjuk T_k-ra a 4 ^oC-os értéket, amit már a 3. ábrán is feltüntettünk.

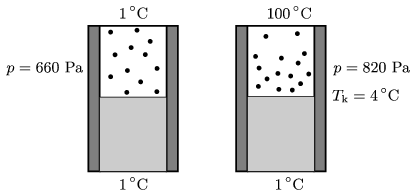
3. ábra

Ezek után a táblázatból extrapolációval kiolvashatjuk a 4 ^oC-hoz tartozó telítési gőznyomás nagyságát: 820 Pa. Ez is szerepel már az ábrán.

Hasonlóképpen kiolvashatjuk a telített vízgőz sűrűségének értékét 4 ^oC-on, ez 6,4 g/m³. A nyomás az egész gőztérben 820 Pa lesz, a gőz sűrűsége azonban csak legalul 6,4 g/m³, felfelé egyre kevesebb. Megbecsülhetjük az átlagos sűrűséget, újra csak ideális gáznak tekintve a vízgőzt, amely átlagosan 50,5 ^oC hőmérsékletű:

\(\displaystyle \varrho=\frac{274}{323{,}5}\cdot6{,}4\,\frac{\rm g}{\rm m^3}=5{,}4\,\frac{\rm g}{\rm m^3}. \)

Ez viszont még mindig több, mint az 1 ^oC-hoz tartozó 5,2 g/m³ érték, vagyis ebben az esetben a gőzállapotban levő vízmolekulák száma nőtt!

Kiegészítés: Számításunkban eltekintettünk a víz sűrűségváltozásától, amely persze elhanyagolható a vízgőz sűrűségváltozásához képest. Mégis okozhat egy kis galibát, ha figyelembe vesszük, hogy a 4 ^oC-os legfelső vízréteg sűrűsége nagyobb, mint az alatta levőké. Ezáltal a víz mechanikailag instabillá válik az edényben, s az egyensúlynak kis megzavarása is áramlásokat idézhet elő. Ha valamelyik versenyző erre is utalt volna a dolgozatában, a versenybizottság plusz pontokkal jutalmazta volna, de senkinek se jutott ez akkor eszébe. Hasonlóképpen figyelmen kívül hagyta mindenki a 100 ^oC-os felső lap hősugárzásának hatását a vízréteg hőmérsékletére, azonban ez a hatás nem is olyan jelentős, hogy módosítaná a végső választ: az a) esetben csökken, a b) esetben nő a vízgőz molekuláinak száma.

3. feladat. Egy toroid (úszógumi) alakú ,,sovány'' vasmagra szimmetrikus elrendezésben három egyforma, ,,kövér'' elektromágneses tekercs van felfűzve a 4. ábra szerint. Az első tekercsre váltóáramú feszültségforrást kapcsolunk, a második tekercs kivezetéseit szabadon hagyjuk, a harmadik tekercs csatlakozóira pedig voltmérőt kötünk. Ekkor a voltmérő a feszültségforrás effektív értékének a felét mutatja.

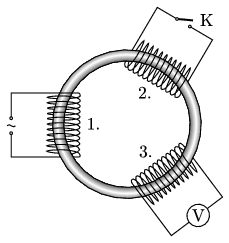
4. ábra

Ezután a második tekercs kivezetéseit a K kapcsolóval rövidre zárjuk. Mit mutat ebben az esetben a voltmérő?

Útmutatás: A tekercsek ohmos ellenállása elhanyagolható, a feszültségforrást és a voltmérőt ideálisnak tekinthetjük. A vasmag mágneses permeabilitása nem függ a mágneses fluxustól.

(Honyek Gyula)

Megoldás. A könnyebb áttekinthetőség végett a tekercseket már a feladat ábráján megszámoztuk.

A szimmetrikus elrendezés miatt (a középiskolai képlettár jelöléseit követve) a tekercsek önindukciós és kölcsönös indukciós együtthatói között az alábbi összefüggéseket írhatjuk fel:

\(\displaystyle L_{11}=L_{22}=L_{33},\text{jelöljük$L$-lel};\)

\(\displaystyle \qquad\qquad L_{12}=L_{21}=L_{13}=L_{31}=L_{23}=L_{32},\text{jelöljük $M$-mel}.\qquad\qquad\)

Tekintsük az egyes tekercsekben indukált feszültségeket! Minthogy I₂=0, mert a kapcsoló nyitva van, valamint I₃\(\displaystyle \approx\)0, mert a voltmérő ellenállása nagyon nagy, csupán az I₁ áram változása indukál feszültséget.

Az 1. tekercsben \(\displaystyle U_{1}=L~\frac{\Delta I_{1}}{\Delta t}\), a 3. tekercsben pedig \(\displaystyle U_{3}=M~\frac{\Delta I_{1}}{\Delta t}\). A feladat szövege szerint \(\displaystyle U_{3}=\frac{U_{1}}{2}\), vagyis \(\displaystyle M=\frac{L}{2}\).

Zárjuk a kapcsolót! Ekkor már a 2. tekercsben is fog áram folyni, vagyis az egyes tekercsekben indukált feszültségek így írhatók fel:

\(\displaystyle U_{1}=L\,\frac{\Delta I_{1}}{\Delta t}+M\,\frac{\Delta I_{2}}{\Delta t},\)

\(\displaystyle U_{2}=M\,\frac{\Delta I_{1}}{\Delta t}+L\,\frac{\Delta I_{2}}{\Delta t},\)

\(\displaystyle U_{3}=M\,\frac{\Delta I_{1}}{\Delta t}+M\,\frac{\Delta I_{2}}{\Delta t}.\)

Azt kell észrevennünk, hogy a rövidzár miatt U₂=0. Ezt felhasználva a két áramváltozási sebesség között adódik egy egyszerű összefüggés:

\(\displaystyle \frac{\Delta I_{2}}{\Delta t}=-\frac{M}{L}\,\frac{\Delta I_{1}}{\Delta t}. \)

Képezzük az \(\displaystyle \frac{U_{3}}{U_{1}}\) hányadost:

\(\displaystyle \frac{U_{3}}{U_{1}}=\frac{M-\frac{M^2}{L}}{L-\frac{M^2}{L}}=\frac{1}{3}. \)

(Az utolsó lépésnél figyelembe vettük, hogy M=L/2).

Tehát a kapcsoló zárása után a voltmérő a feszültségforrás effektív értékének harmadát fogja mutatni.

Kiegészítés: A vasmag permeabilitásának állandóságát akkor használtuk fel, amikor feltételeztük a tekercsek induktivitásának és a kölcsönös indukciós együtthatóknak az állandóságát, vagyis hogy pl. M=L/2 akkor is fennáll, ha zárjuk a kapcsolót. Szokatlan volt a feladatban, hogy ebben a tipikusan transzformátoros összeállításban a feszültségek aránya lényegesen eltér a menetszámok arányától. A mindennapi gyakorlatban ez jól ismert jelenség, inkább az tekinthető idealizációnak, hogy az említett két arány megegyezik. A mágneses mező ,,kiszóródása'' a vasmagból általában elkerülhetetlen, ha nem is olyan jelentős mindig, mint most, ebben a feladatban.

A verseny eredménye

Első díjat és 30 ezer forint pénzjutalmat vehetett át Budai Ádám, a BME fizika BSc szakos hallgatója, aki a miskolci Földes Ferenc Gimnáziumban érettségizett mint Bíró István tanítványa; olimpiai szakkörvezetője Zámborszky Ferenc volt.

Második díjat és 20 ezer forint pénzjutalmat hárman kaptak: Jéhn Zoltán, a BME fizika BSc szakos hallgatója, aki Pécsett, a PTE Babits Mihály Gyakorló Gimnáziumban érettségizett, tanára a gimnáziumban Koncz Károly, az olimpiai szakkörön Kotek László volt; Kalina Kende, a ELTE matematika BSc szakos hallgatója, aki a Fazekas Mihály Fővárosi Gyakorló Gimnáziumban érettségizett Horváth Gábor, Csefkó Zoltán és Szokolai Tibor tanítványaként; Szabó Attila, a pécsi Leőwey Klára Gimnázium 11. évf. tanulója, tanára a gimnáziumban Simon Péter, az olimpiai szakkörön Kotek László.

Harmadik díjat és 15-15 ezer forint pénzjutalmat vehetett át két versenyző: Bolgár Dániel, a pécsi Leőwey Klára Gimnázium 12. évf. tanulója, tanárai Almási László és Simon Péter; Kovács Péter, az ELTE Apáczai Csere János Gyakorló Gimnáziumának 12. évf. tanulója, Pákó Gyula tanítványa.

Hárman kaptak dicséretet és 10-10 ezer forint értékű könyvjutalmat: Batki Bálint, a BME fizika BSc szakos hallgatója, aki az ELTE Apáczai Csere János Gyakorló Gimnáziumban érettségizett mint Zsigri Ferenc tanítványa; Forman Ferenc, az ELTE Radnóti Miklós Gyakorló Gimnáziumának 10. évf. tanulója, Honyek Gyula tanítványa; Jenei Márk, a Fazekas Mihály Fővárosi Gyakorló Gimnázium 11. évf. tanulója, Dvorák Cecília és Csefkó Zoltán tanítványa.

Ünnepélyes díjkiosztás

2011. november 25-én délután 3 órai kezdettel került sor az ünnepélyes eredményhirdetésre és díjkiosztásra. A már jól bevált hagyományt követve először az 50, majd a 25 évvel ezelőtti Eötvös-verseny feladatainak felidézésére került sor. Az akkori nyertesek közül többen is eljöttek, szóltak néhány szót emlékeikről, azóta befutott pályájukról.

Zakariás László 1961-ben a piaristáknál érettségizett. Az Elektronikus Mérőkészülékek Gyárának dolgozójaként nyerte meg az Eötvös-versenyt, mivel a BME-re nem vették fel. Így emlékezett vissza a fél évszázaddal ezelőtt történtekre: ``A Műszaki Egyetemre második próbálkozásra se vettek fel. Fellebbeztünk. A fellebbezést elutasították. A minisztériumi fellebbezéshez csatoltuk az Eötvös-verseny eredményét. Szeptember végén, a születésnapomon, levél érkezett a minisztériumból: Örömmel értesítjük, hogy felvételt nyert a Budapesti Műszaki Egyetem Villamosmérnöki Karára. Én voltam a világ legboldogabb embere. Tisztelettel és hálával gondolok Kovács Mihály tanár úrra.'' Fritz József Mosonmagyaróvárról fizikusnak jelentkezett az ELTE-re, Molnár Emil a győri Révai Gimnáziumból matematika-fizika szakos tanárnak. Mindkettőjüket felvették. Fritz József ma már matematikus akadémikus, Molnár Emil a BME Geometria tanszékének vezetőjeként ment nyugdíjba. Mindhárman hálával emlékeztek vissza tanáraikra, akik megszerettették velük a fizikát, a matematikát, felkészítették őket a versenyre.

A 25 évvel ezelőtti Eötvös-versenynek két első helyezettje volt: Kaiser András és Kohári Zsolt. Mindketten eljöttek, szóltak is a mai nyertesekhez. A többi díjazott közül Drasny Gábor és Gyuris Viktor az Egyesült Államokból levélben üdvözölték a sikeres versenyzőket és dicsérték egykori fizikatanárukat, Horváth Gábort. Leveleiket a versenybizottság tagjai olvasták fel.

Az idei Eötvös-verseny díjait Kroó Norbert akadémikus, az Eötvös Loránd Fizikai Társulat elnöke, Kürti Jenő professzor, a Társulat főtitkára és a verseny lebonyolítását és díjait anyagilag támogató MOL képviseletében Csernik Kornél adta át.

A díjazott versenyzők tanárai a Vince Kiadó és a Typotex Kiadó könyvei közül válogathattak, és jelentős kedvezménnyel vehetnek majd részt a 2012. évi Fizikatanári Ankéton.

Az ünnepélyes díjkiosztást követő, a RAMOSOFT Zrt. támogatásával lebonyolított, jó hangulatú állófogadás résztvevői között ott voltak nemcsak az idei, a 25 és 50 évvel ezelőtti díjazottak, de megjelent a 49 évvel ezelőtti Eötvös-verseny egyik nyertese is.

Remélhetőleg jövőre is találkozhatunk vele.