A 43. Nemzetközi Matematikai Diákolimpia feladatainak megoldásai

A hagyományoknak megfelelően ebben az évben is közöljük a nyári matematikai diákolimpia feladatainak a megoldásait úgy, ahogyan a legilletékesebbek, a magyar csapat tagjai leírták. Közreműködésüket köszönjük és ezúton is gratulálunk eredményeikhez.

A szerkesztőség

1. Legyen n pozitív egész szám. Legyen T a sík azon (x,y) pontjainak halmaza, amelyekre x és y nemnegatív egész számok és x+y<n. T minden pontját pirosra vagy kékre színezzük. Ha az (x,y) pont színe piros, akkor T minden olyan (x',y') pontjának a színe is piros, amelyre x'$\displaystyle \le$x és y' $\le$ y mindegyike teljesül. Nevezzük X-halmaznak az olyan halmazokat, amelyek n olyan kék pontból állnak, amelyek x-koordinátái mind különbözőek, és nevezzük Y-halmaznak az olyan halmazokat, amelyek n olyan kék pontból állnak, amelyek y-koordinátái mind különbözőek.

Bizonyítsuk be, hogy az X-halmazok száma megegyezik az Y-halmazok számával.

Gerencsér Balázs megoldása. A T halmaz adott színezésére jelölje |X| és |Y| az X-halmazok, illetve az Y-halmazok számát. |X| értéke nyilván az adott x-koordinátájú, a színezés nyomán kialakuló háromszög alakú mintázat egyes ,,oszlopaiban'' lévő kék pontok számának a szorzata. (Ha egy oszlopban nincs kék pont, akkor a megfelelő tényező és így a szorzat értéke is 0, összhangban azzal, hogy ilyenkor természetesen nem jön létre X-halmaz.) Hasonlóan kapjuk |Y| értékét az egyes sorokban lévő kék pontok elemszámának a szorzataként.

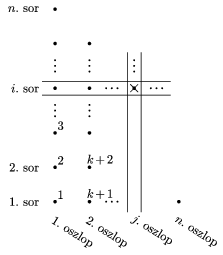
A balról legszélső oszloppal kezdve számozzuk most meg a piros pontokat, az egyes oszlopokban alulról felfelé haladva. Ha egyáltalán nincsen piros pont, akkor az ábra szimmetriája miatt nyilvánvalóan teljesül az állítás. Induljunk ki tehát az ,,azonosan kék'' mintázatból, és számozásunknak megfelelően fessük át a megfelelő kék pontokat egyesével pirosra. Megmutatjuk, hogy |X| és |Y| minden lépésben ugyanúgy változnak, ebből a bizonyítandó állítás nyilván következik.

Ha a (j;i) koordinátájú P pont - ami az i-edik sor és a j-edik oszlop közös eleme - színét változtatjuk kékről pirosra, akkor mivel a számozás szerkezete követi a piros pontoknak a feltételben megadott elrendezését, a P-től balra, illetve lefelé lévő valamennyi pont már piros. P(j;i) átfestésekor |X| csak a j-edik oszlop miatt változik. Ebben az oszlopban összesen n+1-j pont van, a piros pontok száma (i-1)-ről i-re nő, a kékeké pedig ennek megfelelően eggyel csökken, (n+2-j-i)-ről (n+1-j-i)-re. Ebben a lépésben tehát |X| értéke $\displaystyle \frac{n+1-i-j}{n+2-i-j}$-szeresére változik.

Az i-edik sorban ezután i és j fölcserélésével hasonlóan kapjuk |Y| értékének a megváltozását: a bizonyítandó állítás most már következik abból, hogy a kapott együttható értéke nem változik ennek a cserének a során.

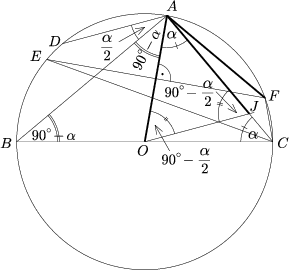
2. Legyen BC az O középpontú $\displaystyle \Gamma$ kör egy átmérője. Legyen A a $\Gamma$ kör egy olyan pontja, amelyre 0^o< AOB $\angle$ < 120^o. Legyen D a C-t nem tartalmazó AB ív középpontja. Az O-n keresztül DA-val párhuzamosan húzott egyenes messe az AC egyenest a J pontban. OA felezőmerőlegesének és $\Gamma$ -nak metszéspontjai legyenek E és F. Bizonyítsuk be, hogy J a CEF háromszög beírt körének a középpontja.

Csikvári Péter megoldása. Legyen BCA$\displaystyle \angle$= $\displaystyle \alpha$. Mivel a feltétel szerint BC a kör átmérője és így a Thalész-tétel miatt BAC$\displaystyle \angle$= 90^o, ezért CBA$\displaystyle \angle$=90^o-$\displaystyle \alpha$. Az egyenlő szárú OAB háromszögben OAB$\displaystyle \angle$= 90^o-$\displaystyle \alpha$ és így az egyenlő szárú OAC háromszögben OAC$\displaystyle \angle$= OCA$\displaystyle \angle$=$\displaystyle \alpha$.

D felezi az AB ívet, így a BD íven feleakkora kerületi szög nyugszik, mint az AB-n: 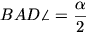$BAD\sphericalangle= \frac{\alpha}{2}$ . Végül mivel 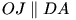$OJ\parallel DA$ , így $\displaystyle DAO\sphericalangle=AOJ\sphericalangle=90^{\circ}- \frac{\alpha}{2}$. (1. ábra)

Tekintsük most az AOJ háromszög szögeit. $\displaystyle AOJ\sphericalangle= 90^{\circ}-\frac{\alpha}{2}$ és OAJ$\displaystyle \angle$= $\displaystyle \alpha$, tehát az AJO$\displaystyle \angle$ szintén 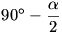$90^{\circ}- \frac{\alpha}{2}$ , a háromszög egyenlő szárú: AO = AJ.


1. ábra	2. ábra

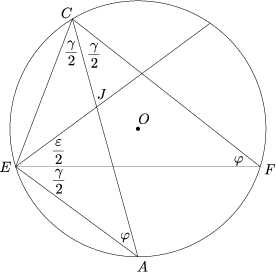
A feltétel szerint EF merőlegesen felezi a kör OA= r sugarát, AEOF tehát r oldalú rombusz. Így r =AF = FO = AO, az utóbbi szakaszról pedig láttuk, hogy AJ-vel egyenlő. Másfelől a fenti rombusz szimmetriája miatt A az EF ív felezőpontja. Ekkor pedig CA felezi az ECF szöget. Megmutatjuk, hogy a fenti két összefüggésből (AJ = AF, illetve CA felezi az ECF szöget) már következik az állítás.

Legyen ECF$\displaystyle \angle$= $\displaystyle \gamma$, ekkor, mint láttuk, 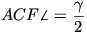$ACF\sphericalangle=\frac{\gamma}{2}$ . Így az AF íven nyugvó AEF$\displaystyle \angle$ ugyancsak $\displaystyle \frac{\gamma}{2}$ (2. ábra; a két ábrán az EFC háromszög nem egybevágó!). Ha $\varphi$ jelöli az EC íven nyugvó kerületi szöget, akkor EFC $\angle$ = EAC$\displaystyle \angle$= $\displaystyle \varphi$.

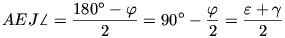Ha most az EFC háromszög harmadik szögét, a CEF szöget $\displaystyle \varepsilon$-nal jelöljük, akkor $\varepsilon$ + $\displaystyle \varphi$+ $\gamma$ = 180^o és EA = AJ miatt $AEJ\sphericalangle=\frac{180^{\circ}-\varphi}{2}= 90^{\circ}-\frac{\varphi}{2}=\frac{\varepsilon+\gamma}{2}$ . Így pedig $\displaystyle FEJ\sphericalangle=AEJ\sphericalangle- AEF\sphericalangle=\left(\frac{\varepsilon+\gamma}{2}\right) -\frac{\varepsilon}{2}=\frac{\gamma}{2}$. Az EJ egyenes tehát felezi a CEF szöget, ezzel pedig két belső szögfelező metszéspontjaként J valóban az EFC háromszög beírt körének a középpontja.

A fenti bizonyítás mindaddig érvényes, amíg J az AC szakasz belső pontja. Ez pedig pontosan akkor teljesül, ha AOJ$\displaystyle \angle$< AOC$\displaystyle \angle$, vagyis 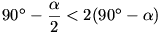$90^{\circ}- \frac{\alpha}{2}<2(90^{\circ}-\alpha)$ . Ez pedig éppen az $\alpha$ < 60^o, azaz a feltételül adott AOB $\angle$ <120^o esetén teljesül.

3. Határozzuk meg az összes olyan (m,n) párt, ahol m, n egész számok, amelyekre m,n$\displaystyle \ge$3, amelyekhez létezik végtelen sok olyan a pozitív egész szám, amire

$\displaystyle \frac{a^m+a-1}{a^n+a^2-1} $

egész szám.

Rácz Béla András megoldása. Legyen p(x) = x^m + x - 1 és q(x) = xⁿ +x² - 1. Először megmutatjuk, hogy ha egy (m, n) párra teljesül a feladat feltétele, akkor a nevező, mint polinom is osztója a számlálónak, azaz q(x)|p(x).

Végezzük ehhez el a p(x) és a q(x) polinomok között a maradékos osztást, azaz legyen p(x)= h(x) ^.q(x) + r(x), ahol a maradék fokszáma kisebb, mint az osztóé, 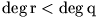$\deg\mathrm{r}< \deg\mathrm{q}$ . Mivel az osztó főegyütthatója 1, ezért mind a hányados, mind pedig a maradék egész együtthatós polinomok.

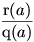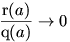A feltétel szerint végtelen sok egész a-ra teljesül, hogy $\displaystyle \frac{\mathrm{p}(a)}{\mathrm{q}(a)}=\mathrm{h}(a)+ \frac{\mathrm{r}(a)}{\mathrm{q}(a)}$ egész szám. Láttuk, hogy az a egész értékeire h(a) egész, így viszont végtelen sok egész a-ra lesz az $\frac{\mathrm{r}(a)}{\mathrm{q}(a)}$ hányados értéke is egész szám. A fokszámok összehasonlításából következik, hogy $\frac{\mathrm{r}(a)}{\mathrm{q}(a)}\to0$ , ez pedig azt jelenti, hogy ennek a hányadosnak az értéke végtelen sok egész a-ra 0. Ugyanez ekkor a számlálóra is teljesül és ha egy polinom végtelen sok helyen veszi fel a 0 értéket, akkor a polinom azonosan nulla. Az r(x) polinom tehát azonosan nulla, a q(x) polinom tehát valóban osztója a p(x) polinomnak.

Ha m < n, akkor nyilván nem állhat fönn a talált oszthatóság. Föltehető ezért, hogy m $\ge$ n. Ekkor a q(x) polinom az

(x + 1) ^.p(x) - q(x) = xⁿ (x^m-n+1 +x^m-n- 1)

polinomnak is osztója. Mivel xⁿ és xⁿ + x² -1 relatív prímek és föltevésünk szerint a második tényező is polinom, ezért innen következik, hogy

xⁿ + x² - 1 |x^m-n+1 + x^m-n - 1.

Vezessük be a k = m - n jelölést. Ekkor k $\displaystyle \ge$0, q(x) = xⁿ + x² - 1 |x^k+1 + x^k-1 és nyilván k + 1 $\ge$ n.

Mivel q(x) folytonos függvény és q(0) < 0 <q(1), azért van olyan 0 < $\alpha$ < 1, hogy q($\displaystyle \alpha$) = 0, azaz $\displaystyle \alpha$ⁿ+ $\alpha$ ² = 1. A q(x)|x^k+1 +x^k-1 oszthatóságot felhasználva innen $\alpha$ ^k+1 + $\displaystyle \alpha$^k= 1 következik. Így tehát

(*)	$\alpha$ ⁿ + $\displaystyle \alpha$² = $\alpha$ ^k+1 + $\displaystyle \alpha$^k = 1.

Ha k = 1, akkor a második egyenlőség semmilyen valós $\displaystyle \alpha$-ra nem teljesülhet. Ha k $\ge$ 2, akkor n $\displaystyle \ge$3 és így a már látott k + 1 $\displaystyle \ge$n feltétellel együtt azt kapjuk, hogy

k $\displaystyle \ge$n - 1 $\displaystyle \ge$2.

Mivel 0 < $\displaystyle \alpha$< 1, innen $\alpha$ ⁿ $\displaystyle \ge$ $\alpha$ ^k+1, illetve $\alpha$ ² $\ge$ $\alpha$ ^k következik. Ez pedig (*) miatt csak akkor teljesülhet, ha $\alpha$ ⁿ = $\alpha$ ^k+1 és $\alpha$ ²= $\alpha$ ^k, vagyis ha n=k +1 és 2 = k, azaz ha m = 5 és n= 3.

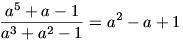Erre a számpárra másfelől a⁵ + a-1 = (a³+a²-1) (a²-a+1). Ha pedig a pozítiv egész, akkor a³+a²-1 $\ge$ 1+1-1 > 0, ezért $\frac{a^5+a-1}{a^3+a^2-1}=a^2-a+1$ , ami minden pozitív egész a-ra egész szám.

Egyetlen olyan számpár van tehát, amelyre teljesülnek a feladat feltételei: az (5; 3).

4. Legyen n 1-nél nagyobb egész szám. n összes pozitív osztója

d₁,d₂,...,d_k, ahol 1=d₁<d₂<...<d_k=n.

Legyen

D=d₁d₂+ d₂d₃+ ...+ d_k-1d_k.

(a) Bizonyítsuk be, hogy D<n².

(b) Határozzuk meg az összes olyan n számot, amire D osztója n²-nek.

Kovács Erika Renáta megoldása. (a) Becsüljük felülről a d_i d_i+1 szorzatokat. Mivel d₁= 1 és d_i < d_i+1, azért i $\le$ d_i. Miután pedig az osztópárokra n = d_j d_(k+1)-j teljesül, ha 1 $\le$ j $\le$ k, így

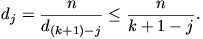
$d_j=\frac{n}{d_{(k+1)-j}}\le\frac{n}{k+1-j}.$

Ebből következik, hogy

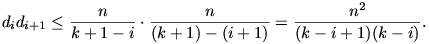
$d_id_{i+1}\le\frac{n}{k+1-i}\cdot\frac{n}{(k+1)-(i+1)}= \frac{n^2}{(k-i+1)(k-i)}.$

Ha összegezzük ezeket az egyenlőtlenségeket, akkor azt kapjuk, hogy

(1)	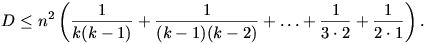$D\le n^2\left(\frac{1}{k(k-1)}+\frac{1}{(k-1)(k-2)}+\dots+ \frac{1}{3\cdot2}+\frac{1}{2\cdot1}\right).$

Mivel 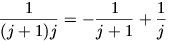$\frac{1}{(j+1)j}=-\frac{1}{j+1}+\frac{1}{j}$ , a zárójelben úgynevezett teleszkopikus összeg áll: értéke

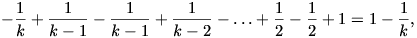
$-\frac{1}{k}+\frac{1}{k-1}-\frac{1}{k-1}+\frac{1}{k-2}- \dots+\frac{1}{2}-\frac{1}{2}+1=1-\frac{1}{k},$

kisebb, mint 1 és pozitív. Ebből pedig (1) felhasználásával a bizonyítandó állítást kapjuk.

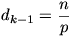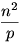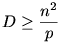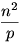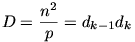(b) Tegyük fel, hogy D |n². Mivel az első rész állítása szerint D = n² nem lehetséges, ezért D valódi osztója n²-nek. Legyen az n legkisebb prímosztója p. Ekkor d₂= p, tehát osztópárja, $d_{k-1}=\frac{n}{p}$ . A d_k-1 d_k szorzat értéke tehát $\frac{n^2}{p}$ és így persze $D\ge\frac{n^2}{p}$ . Mármost p választása szerint n² legnagyobb valódi osztója éppen $\frac{n^2}{p}$ , így ha D|n², akkor $D=\frac{n^2}{p}=d_{k-1}d_k$ !

Így a k értéke 2, tehát p=d₂=d_k=n, az n egyenlő a legnagyobb prímosztójával, vagyis maga is prím. Az pedig nyilvánvaló, hogy ha n tetszőleges prímszám, akkor D=n, ami osztója n²-nek.

5. Határozzuk meg az összes olyan f függvényt, ami a valós számok R halmazát önmagába képezi és amelyre

(f(x)+f(z)) (f(y)+f(t))= f(xy-zt)+ f(xt+yz)

teljesül minden x,y,z,t $\in$ R esetén.

Harangi Viktor megoldása. Helyettesítsünk az egyenletben mind a négy változó helyére u-t: azt kapjuk, hogy minden u valós számra

(1)	4f²(u) = f(0) + f(2u²).

Ha most u=0, akkor 4f²(0) = f(0)+f(0) = 2f(0). Innen rendezés után

f(0)(2f(0)-1) = 0,

azaz vagy f(0)=0 vagy pedig 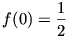$f(0)=\frac{1}{2}$ .

Vizsgáljuk először a második esetet.

Végezzük el az eredeti függvényegyenletben az y=t=0, z=x helyettesítéseket:

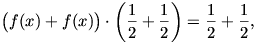
$\big(f(x)+f(x)\big)\cdot\left(\frac{1}{2}+ \frac{1}{2}\right)=\frac{1}{2}+\frac{1}{2},$

ahonnan 2f(x)=1, azaz 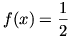$f(x)=\frac{1}{2}$ , erre a függvényre pedig nyilvánvalóan teljesül a feladat függvényegyenlete.

Tekintsük ezután az f(0)=0 lehetőséget.

Ha a z és a t változók helyére 0-t írunk, akkor a minden valós x, y számpárra fennálló

(2)	f(x) ^.f(y) = f(xy)

egyenlőséget kapjuk, az f függvény tehát ebben az esetben multiplikatív.

Az (1) egyenlet most 4f²(u) = f(2u²) alakú, tehát ha 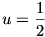$u= \frac{1}{2}$ , akkor

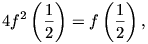
$4f^2\left(\frac{1}{2}\right)=f\left(\frac{1}{2}\right),$

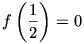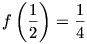ahonnan $f\left(\frac{1}{2}\right)=0$ , vagy $f\left(\frac{1}{2}\right)=\frac{1}{4}$ .

Az első esetben (2) felhasználásával kapjuk, hogy minden valós x-re

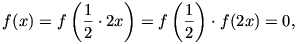
$f(x)=f\left(\frac{1}{2}\cdot2x\right)=f\left( \frac{1}{2}\right)\cdot f(2x)=0,$

az azonosan nulla függvény pedig nyilván megoldása az eredeti függvényegyenletnek.

Hátravan még a második lehetőség, az 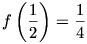$f\left(\frac{1}{2}\right)= \frac{1}{4}$ eset vizsgálata (természetesen az f(0)=0 feltétellel együtt). Ekkor

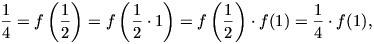
$\frac{1}{4}=f\left(\frac{1}{2}\right)=f\left(\frac{1}{2}\cdot1\right)= f\left(\frac{1}{2}\right)\cdot f(1)=\frac{1}{4}\cdot f(1),$

vagyis f(1)=1. (Itt és a továbbiakban az f multiplikativitását külön hivatkozás nélkül használjuk.)

A talált összefüggésből következik, hogy ha u tetszőleges nem nulla valós szám, akkor

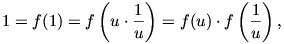
$1=f(1)=f\left(u\cdot\frac{1}{u}\right)=f(u)\cdot f\left(\frac{1}{u}\right),$

tehát f(u) sem nulla. Így

(3)	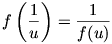$f\left(\frac{1}{u}\right)=\frac{1}{f(u)}$

teljesül tetszőleges u $\ne$ 0 valós számra. Legyen most az eredeti egyenletben y=t=1. Ekkor

2f(x)+2f(z) = f(x-z) + f(x+z),

azaz

(4)	f(x+z) = 2[f(x)+f(z)] - f(x-z).

Az eddig talált f(0) = 0², f(1) = 1² - valamint (2), (3) és (4) - kellő önbizalmat adhat az eredmény kiterjesztéséhez. Pozitív egészekre használjunk indukciót: legyen k> 1 egész szám és tegyük fel, hogy az f függvény a k-nál kisebb nemnegatív egészeken a behelyettesített érték négyzetét veszi fel. Lássuk be, hogy ekkor f(k) = k² is igaz. Valóban, (4) és az indukciós föltevés szerint

f(k) = 2 [f(k-1) + f(1)] - f(k-2) = 2((k-1)²+1)- (k-2)² = k².

Pozitív racionális számokra ezután (2) és (3) alapján teljesen szokványos módon

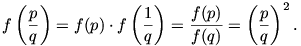
$f\left(\frac{p}{q}\right)=f(p)\cdot f\left(\frac{1}{q}\right)= \frac{f(p)}{f(q)}=\left(\frac{p}{q}\right)^2.$

Negatív számokra alakítsuk át (4)-et: írjunk x helyére 0-t: f(z) = 2[f(z)] - f(-z), azaz minden z valós számra

(5)	f(-z) = f(z),

f páros függvény és így eddigi eredményeink szerint minden x racionális számra f(x)=x². A megoldás befejező részében, amint az várható, ezt terjesztjük ki a valós számok halmazára. Ehhez a talált algebrai összefüggések mellett határátmenet meggondolásokra lesz szükség.

Először - egy ,,közbeiktatott lépéssel'' - azt mutatjuk meg, hogy nullától különböző értékekre a függvény pozitív. Ha x > 0, akkor

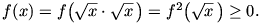
$f(x)=f\big(\sqrt x\cdot\sqrt x\,\big)=f^2\big(\sqrt x\,\big) \ge0.$

Láttuk másfelől, hogy 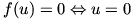$f(u)=0\Leftrightarrow u=0$ és így f(x) pozitív, ha x > 0. Mivel pedig a függvény páros, ebből már valóban következik, hogy minden nullától különböző helyen pozitív értéket vesz föl.

Most megmutatjuk, hogy a pozitív számok halmazán az f függvény szigorúan monoton növő. Tekintsük ehhez - utoljára - az eredeti egyenletet és legyen ott t=x és z=y.

Azt kapjuk, hogy [f(x) + f(y)]² = f(x²+y²), ahonnan

f(x²+y²) - f(x²) = [f(x)+f(y)]² - f(x) ^.f(x) =f²(y) + 2f(x) ^.f(y),

ami pedig határozottan pozitív, ha y nem nulla. Legyenek most 0 $\le$ a < b tetszőleges valós számok. Ekkor nyilván léteznek olyan x, y valós számok, amelyekre a=x², b=x²+y² és y $\ne$ 0. A fentiek szerint ekkor f(b) -f(a) > 0, tehát az f függvény valóban szigorúan monoton növő a pozitív valós számok halmazán. Így persze szigorúan monoton fogyó, ha x negatív.

A még hiányzó irracionális helyeken a mindenütt sűrűn elhelyezkedő racionális számokat használjuk fel. Ismeretes, hogy egy szigorúan monoton növő függvénynek mindenütt létezik bal-, illetve jobboldali határértéke. Ha x tetszőleges irracionális szám, akkor egy-egy x-hez balról, illetve jobbról tartó racionális számokból álló sorozaton a függvényértékek sorozata mindkét esetben x²-hez tart, hiszen racionális számokra f(u)=u². Az f bal- és jobboldali határértéke tehát egyaránt x²-tel egyenlő az x-helyen, így mivel szigorúan monoton, az f itt folytonos és így f(x)=x² akkor is fennáll, ha x irracionális szám.

Az adott függvényegyenlet tehát három függvényre teljesülhet; ezek:

f(x) = 0, 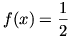$f(x)=\frac{1}{2}$ és f(x)=x².

Mindhárom függvény nyilvánvalóan kielégíti az egyenletet.

6. Legyenek $\Gamma$ ₁, $\Gamma$ ₂, ..., $\Gamma$ _n egységsugarú körök a síkban, ahol n $\ge$ 3. Jelölje a középpontjaikat rendre O₁,O₂,...,O_n. Tegyük fel, hogy nincs olyan egyenes, aminek kettőnél több körrel van közös pontja. Bizonyítsuk be, hogy

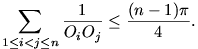
$\sum_{1\le i<j\le n}\frac{1}{O_iO_j}\le\frac{(n-1)\pi}{4}.$

Csóka Endre megoldása. Először is jegyezzük meg, hogy egy egyenesnek és $\Gamma$ _i-nek pontosan akkor van közös pontja, ha O_i legfeljebb egységnyi távolságra van az egyenestől. A feltétel tehát úgy fogalmazható, hogy nincs a síkon olyan egyenes, amelyik az O₁,O₂,...,O_n pontok közül háromtól is legfeljebb egységnyi távolságra halad. Ez azt is jelenti, hogy semelyik három középpont nincs egy egyenesen.

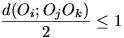Jelöljük a sík egy tetszőleges P pontjának és e egyenesének a távolságát d(P;e)-vel. Ha létezne olyan három középpont, amelyekre d(O_i;O_j O_k) $\le$ 2 (i, j, k különbözők), akkor az O_i O_j O_k háromszög O_j O_k-val párhuzamos középvonala $\frac{d(O_i;O_jO_k)}{2}\le1$ távolságra lenne a három középpont mindegyikétől. Láttuk, hogy ezt a feltétel kizárja, azért bármelyik középpont legalább 2 egységnyi távolságra van bármely két további középponton átmenő egyenestől. Ezen az észrevételen múlik a feladat megoldása, a továbbiakban azonban még igen fáradságosan kell ,,megdolgoznunk'' azért, hogy az adott formában kapjuk meg az állítást.

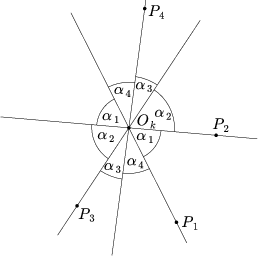
Adott O_k középpontra tekintsük a további n-1 középpontnak azt a P₁,P₂, ...,P_n-1 sorrendjét, amelyben egy az O_k körül pozitív irányba forgó egyenes áthalad rajtuk. Ez a sorrend egyértelmű, hiszen nincsen három kollineáris középpont. (Az indexelést mod (n-1) végezzük.) Legyen még $\alpha$ _i az a legkisebb forgásszög, amellyel az O_kP_i egyenest az O_k körül pozitív irányban elforgatva az O_kP_i+1 egyenest kapjuk. (1. 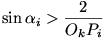ábra) Ekkor az $\alpha$ _i szögek összege nyilván $\pi$ , másfelől d(P_i+j;O_k,P_i ) > 2 miatt $\sin\alpha_i>\frac{2}{O_kP_i}$ . A minden pozitív számra fennálló x > sin x egyenlőtlenséget is felhasználva kapjuk, hogy

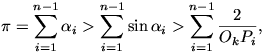
$\pi=\sum_{i=1}^{n-1}\alpha_i>\sum_{i=1}^{n-1} \sin\alpha_i>\sum_{i=1}^{n-1}\frac{2}{O_kP_i},$

tehát

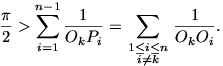(1)	$\frac{\pi}{2}>\sum_{i=1}^{n-1}\frac{1}{O_kP_i}= \sum_{\scriptstyle{1\le i\le n}\atop\scriptstyle{i\ne k}}\frac{1}{O_kO_i}.$


1. ábra	2. ábra

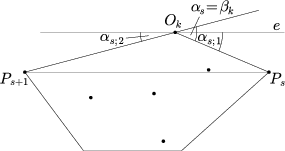
Ha O_k a középpontok konvex burkának $\beta$ _k külsőszögű pontja (2. ábra), akkor jelölje P_s és P_s+1 a konvex burok O_k-val szomszédos csúcsait. (Ezek különbözők, hiszen n $\ge$ 3.) Ekkor nyilván $\beta$ _k = $\alpha$ _s. Az O_k-n átmenő P_sP_s+1 egyenessel párhuzamos e egyenesre legyenek $\alpha$ _s;1 és $\alpha$ _s;2 rendre az e és az O_kP_s illetve az e és az O_kP_s+1 egyenesek által bezárt szögek közül azok, amelyek összege $\alpha$ _s. Mivel

2 < d(O_k;P_s P_s+1) = d(P_s;e) = d(P_s+1;e),

azért

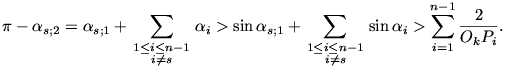
$\pi-\alpha_{s;2}=\alpha_{s;1}+ \sum_{\scriptstyle{1\le i\le n-1}\atop\scriptstyle{i\ne s}} \alpha_i>\sin\alpha_{s;1}+ \sum_{\scriptstyle{1\le i\le n-1}\atop\scriptstyle{i\ne s}} \sin\alpha_i>\sum_{i=1}^{n-1}\frac{2}{O_kP_i}.$

Ugyanezt a becslést a másik körüljárás szerint is elvégezve 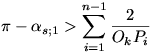$\pi-\alpha_{s;1}>\sum_{i=1}^{n-1}\frac{2}{O_kP_i}$ adódik. Adjuk össze ezt a két egyenlőtlenséget:

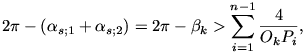
$2\pi-(\alpha_{s;1}+\alpha_{s;2})=2\pi-\beta_k> \sum_{i=1}^{n-1}\frac{4}{O_kP_i},$

azaz

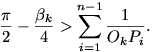(2)	$\frac{\pi}{2}-\frac{\beta_k}{4}>\sum_{i=1}^{n-1} \frac{1}{O_kP_i}.$

Összegezzük végül a középpontok konvex burkának belső pontjaira az (1), a csúcsaira pedig a (2) becslést:

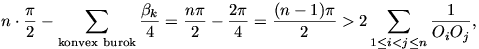
$n\cdot\frac{\pi}{2}-\sum_{\rm konvex~burok} \frac{\beta_k}{4}=\frac{n\pi}{2}-\frac{2\pi}{4}=\frac{(n-1)\pi}{2} >2\sum_{1\le i<j\le n}\frac{1}{O_iO_j},$

ahonnan 2-vel osztva éppen a bizonyítandó állítást - pontosabban annak egy élesebb formáját - kapjuk.

Beszámoló a 43. Nemzetközi Matematikai Diákolimpiáról

A 43. Nemzetközi Matematikai Diákolimpia honlapja

Nemzetközi Matematikai Diákolimpiák

Beszámoló a 42. Nemzetközi Matematikai Diákolimpiáról

Már regisztráltál?
Új vendég vagy?