Géza Kós
Dogs from Planet Mars
(Published in KöMal, 1996/3, pp. 138-144.)
The game to be introduced here was invented by Eward Fradkin. First of all we describe the rules of the game.
Imagine that the world is an infinitely large squared sheet of paper and there are cells living in certain squares. One square can contain one cell at most at a time. We represent the position of the cells by colouring all squares which contain a cell.
Every minute all cells are divided into four descendants who will live in the adjoining four squares (the original cell disappears). If a square happens to contain more than one cell after the division of cells then those cells destroy each other in pairs, and finally 1 or 0 of them will remain in the square. This means that in a fixed generation a square will contain a cell if and only if 1 or 3 of the adjoining squares contained a cell in the previous generation.

Figure 1
Figure 1 represents the first few generations if we start with one cell.
There is a slightly different way of deriving these positions. Suppose that any number of cells can live in a square; they do not destroy each other. We colour each square that contains an odd number of cells. It is easy to see that in this way we will arrive at the same positions as before.
This reformulation is very useful. If the starting position consists of more than one cell and we want to see the situation after n generations then we can first calculate the number of descendants for each starting cell and then we can add up the numbers in each square.
What happens with the formations when we add up the numbers? Those squares will be coloured which are coloured for n odd number of starting cells. We can call this the addition of formations. Figure 2 illustrates this addition for two starting cells.

Figure 2
Another important property of the game is that after 2n generations one starting cell will always have four descendants. These lie at the distance of 2n squares from the position of the starting cell, one to the left, one to the right, one upwards, and one downwards. This can be proved by induction. When n=0, 2n=1 and after 1 generation we do have the required formation by the rule set for the division of cells. Suppose we have the required formation of four cells after 2n generations. Now, after another 2n generations these four cells will produce 16 descendants altogether, and it is easy to see that 12 of these will destroy each other and the remaining 4 will give the required formation.

Figure 3
Let us form a small `picture', e.g. a dog, out of a few cells. After 2n generations each cell of the dog will have four descendants as we described above. These descendants will form four different dogs. If n is small these dogs can interfere with each other and the picture can easily be unrecognisable. However, if n is large enough, then the four dogs do not interfere, they stand aparr. If n is not a power of 2 but is divisible by a `large enough' power of two (e.g. 12 is divisible by 4) then after n generations we will have more than four dogs in the picture. (See Figure 3.)
Computer Program I
The simulation of the game on computer raises an interesting problem. The computer cannot simulate an infinitely large sheet of paper, it can only work in a finite rectangle. This means that the cells along the sides of the rectangle will only have three descendants and those at the corners will only have two.
What will the effects of this slight change be?
This applet below illustrates the game in a rectangle of size 25x39.
Examining the generations, we see an interesting phenomenon. Besides the dogs we are used to seeing, their mirror images come into the picture, too: dogs standing upside down or looking left instead of right. It looks as if they had been reflected back from the sides of the rectangle.
The reason for this phenomenon lies in the slight alteration in the rule of division of cells at the sides of the rectangle. They divide into fewer descendants and the descendants of the missing descendants will be missing too. It is very difficult, however, to trace down the effects of missing descendants generation by generation. We need a more general method of determining what will happen.
The Principle of Reflection
In order to understand what actually happens at the sides of the rectangle, let us first consider a slightly simpler case. Imagine that the world now is only half of the plane bordered by a vertical line. As we have seen, if we change the rules of division of cells along the border-line we will not be able to trace down the consequences. Therefore, we will pretend, instead, that the world is still the whole plane but only half of it is visible to us. Suppose that the cells along the border-line of the visible world divide into four just like any other cells, but one of their descendants (namely the one that would live beyond the border-line) dies immediately for some unknown reason. The reason must be sought in the invisible part of the world. Maybe some cells live there too which we cannot see, but the effects of which we can observe.
Our task is to put cells into the invisible half of the world such that their descendants destroy those descendants of the cells in the visible world which would live in the invisible half. In this way we can simulate that the cells along the border-line have only three descendants. The task is easy to solve. We take the column in the invisible half along the border-line, and we put the reflection of our picture with respect to this column into the invisible world. (See Figure 4.)
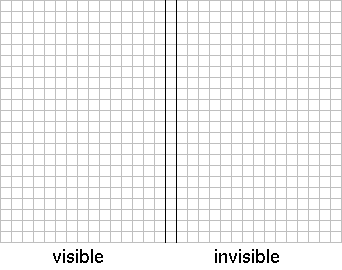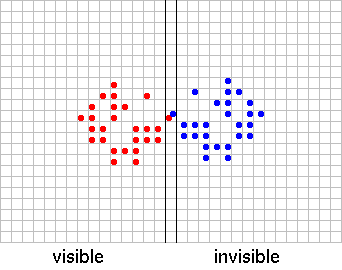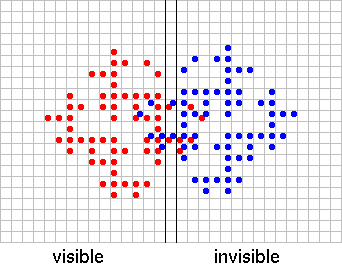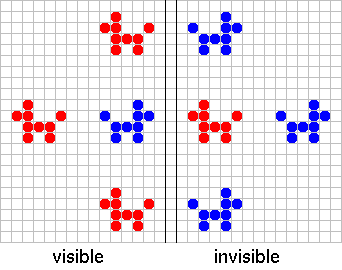
Figure 4
The position of the cells is always symmetrical to the middle column so cells will always come in pairs into the column and they will destroy each other.
After a few generations the descendants of cells of the invisible dog will appear in the visible world.
As we saw in the first part of the article both dogs produced four `descendants' but we can only see four of the eight descendants. Three descendants of the original and one of the reflected dog are visible to us. So, of the four visible dogs only three originate from the original dog, one (the one looking to the right) has come from the invisible world.
When the world is only a rectangle the situation is more complicated. The principle of reflection has to be applied in a more complicated way. Consider the two rows and two columns that border the rectangle from outside. We need to put cells into the rest of the plane in such a way that our picture be symmetrical with respect to all four border-lanes. This can be done as pictured in Figure 5.
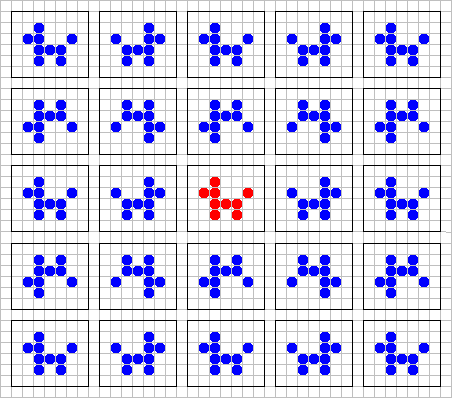
Figure 5
The descendants of different dogs sometimes appear in the rectangle which we can actually see. So, that is where all the different dogs come from.
Exercises
1.) What happens if the world is not a rectangle but an isosceles right angled triangle (the hypotenuse of which forms a `stair')?
2.) What if the cells divide into nine descendants, one of which remains in the original square and the other eight go to the squares sharing a common vertex with the original square?
3.) Suppose that each cell divides into n descendants and their positions are given by vectors \(\displaystyle nu\)1,\(\displaystyle nu\)2,...,\(\displaystyle nu\)n originating from the original square. Prove that after two generations the number of descendants will still be n and their positions will be given by vectors 2\(\displaystyle nu\)1,2\(\displaystyle nu\)2,...,2\(\displaystyle nu\)n.
4.) Let the world be a rectangle of size nxk. Prove that if n+1 and k+1 are powers of 2 then whatever picture we start from, all the cells will die out sooner or later.
5.) What happens if the cells destroy each other not in pairs but in triplets? How does it affect the principle of reflection?
6.) Let the world be a rectangle of size nxk, and suppose that whatever picture we start from all the cells die out sooner or later. Prove that either n=k=2 or both n+1 and k+1 are powers of 2.
Computer Program II
By the next applet many interesting problems can be considered and the answers of the exercises in the previous section can be demonstrated. We suggest to try the program after solving the exercises.
On the right side the rules of division and dsrtoying can be selected.
Clicking on the board, the content of the fields - the initial state - can be set. All fields can be set to contain 0, 1 or 2 cells or a wall.
