A 2001. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldása
1. Adott a síkon 3n-1 pont, közülük semelyik három nem esik egy egyenesre. Mutassuk meg, hogy található közöttük 2n pont, melyek konvex burka nem háromszög.
I. Megoldás. Ha n=1, akkor az állítás nyilvánvaló, n>1 esetén pedig ekvivalens azzal, hogy található 2n pont, melyek konvex burkának legalább 4 csúcsa van. Ha találunk m\(\displaystyle ge\)2n pontot, melyek konvex burkának legalább 4 csúcsa van, azok közül már könnyűszerrel elhagyhatunk m-2n pontot úgy, hogy a megmaradók konvex burkának még mindig legalább 4 csúcsa legyen.
Ha a pontok P halmazának konvex burka nem háromszög, akkor a
fenti megjegyzés értelmében készen is vagyunk. Feltehető tehát, hogy
P konvex burka egy
A1B1C1
háromszög. Tegyük fel, hogy valamely i<n esetén az
A1,...,Ai pontokat már
definiáltuk úgy, hogy minden j\(\displaystyle le\)i esetén a 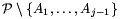 ponthalmaz konvex burka éppen az
AjB1C1
háromszög. A \(\displaystyle {\cal P}\setminus\{A_1,\ldots,A_{i}\}\) halmaznak legalább
2n pontja van, ezért az előbbi megállapításunkhoz hasonlóan
feltehetjük, hogy e halmaz konvex burka is egy háromszög. Ennek két
csúcsa nyilván B1 és C1, a
harmadikat jelöljük Ai+1-gyel.
ponthalmaz konvex burka éppen az
AjB1C1
háromszög. A \(\displaystyle {\cal P}\setminus\{A_1,\ldots,A_{i}\}\) halmaznak legalább
2n pontja van, ezért az előbbi megállapításunkhoz hasonlóan
feltehetjük, hogy e halmaz konvex burka is egy háromszög. Ennek két
csúcsa nyilván B1 és C1, a
harmadikat jelöljük Ai+1-gyel.
Megállapíthatjuk tehát, hogy ha nem található a pontok között
2n olyan, melyek konvex burka nem háromszög, akkor létezik egy
A1,A2,...,An
pontsorozat P-ben úgy, hogy minden i n esetén
\(\displaystyle {\cal
P}\setminus\{A_1,\ldots,A_{i-1}\}\) konvex burka az
AiB1C1
háromszög. Hasonlóan készíthetjük el a
B1,B2,...,Bn
és
C1,C2,...,Cn
pontsorozatokat is. Az így kapott 3n pont között kell legyen
kettő olyan, amelyik egybeesik. Az általánosság megszorítása nélkül
feltehetjük, hogy
Aj=Bk. Ekkor a
n esetén
\(\displaystyle {\cal
P}\setminus\{A_1,\ldots,A_{i-1}\}\) konvex burka az
AiB1C1
háromszög. Hasonlóan készíthetjük el a
B1,B2,...,Bn
és
C1,C2,...,Cn
pontsorozatokat is. Az így kapott 3n pont között kell legyen
kettő olyan, amelyik egybeesik. Az általánosság megszorítása nélkül
feltehetjük, hogy
Aj=Bk. Ekkor a
\(\displaystyle {\cal P}\setminus\{A_1,A_2,\ldots,A_n\}\setminus\{B_1,B_2,\ldots,B_n\}\setminus\{C_1\}\)
ponthalmaznak legalább n-1\(\displaystyle ge\)1 pontja van, és mindegyik belső pontja mind az AjB1C1, mind a BkA1C1 háromszögnek. Ez azonban lehetetlen, hiszen a két háromszögnek nincs közös belső pontja. Ez az ellentmondás igazolja az állítást.
Megjegyzések. 1. Nem nehéz megmutatni, hogy a feladatban 3n-1 helyébe 3n-2 már nem írható. Valóban, legyen A1B1C1 egy szabályos háromszög, melynek középpontja O, és legyen A, B, C rendre az OA1, OB1 és OC1 szakaszok felezőpontja. Legyen kA, kB és kC egy-egy R sugarú körív, mely az A1 és A, B1 és B, illetve C1 és C pontokat köti össze. Vegyük fel a kA, kB, kC íveken az A2,...,An, B2,...,Bn-1 és C2,...,Cn-1 pontokat. Ha n\(\displaystyle ge\)2 és R elég nagy, akkor a P={A1,...,An,B1,...,Bn-1,C1,...,Cn-1} 3n-2 elemű ponthalmazból nem választható ki 2n pont, melyek konvex burka nem háromszög. Ha ugyanis R elég nagy, akkor minden AiAj egyenes elválasztja egymástól a Bk és C\(\displaystyle ell\) pontokat. Ha tehát P egy részhalmaza konvex burkának csúcsa az Ai és Aj pont is, akkor az A1,...,An pontokon kívül legfeljebb n-1 további pontot tartalmazhat, tehát legfeljebb 2n-1 pontja lehet. Hasonlóképpen okoskodhatunk akkor is, ha a konvex burok a Bi vagy a Ci pontok közül tartalmaz legalább kettőt csúcsként. Következésképpen P minden 2n elemű részhalmazának konvex burka mind az Ai, mind a Bi és úgyszintén a Ci pontok közül is csak egyet tartalmazhat csúcsként, és így szükségképpen háromszög lesz.
2. Jelölje \(\displaystyle \lceil x\rceil\) az x valós szám fölső egész részét, vagyis az x-nél nem kisebb egész számok közül a legkisebbet. Megmutatható, hogy az alábbi erősebb állítás is igaz.
Tegyük fel, hogy n\(\displaystyle ne\)3, és adott a síkon 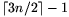 pont, melyek közül semelyik három nem
esik egy egyenesre. Ekkor található közöttük n pont, melyek konvex
burka nem háromszög.
pont, melyek közül semelyik három nem
esik egy egyenesre. Ekkor található közöttük n pont, melyek konvex
burka nem háromszög.
A következőkben erre az állításra adunk még két
bizonyítást. Jegyezzük meg, hogy a feltételnek csak akkor van értelme,
ha n pozitív egész szám, és hogy n\(\displaystyle le\)2 esetén az állítás nyilván igaz. Ennek
megfelelően a megoldások során feltesszük, hogy n>3 egész
számot jelöl. Páratlan n esetén a fenti konstrukció apró
módosításával ellenőrizhetjük azt is, hogy ha a pontok száma 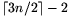 , akkor az állítás már nem marad igaz.
, akkor az állítás már nem marad igaz.
II. Megoldás. Tegyük fel, hogy a P legalább 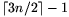 elemű általános helyzetű ponthalmaz nem
tartalmaz n pontot, melyek konvex burka nem háromszög. Legyen
P konvex burka az ABC háromszög, és legyen
A1=A. Az első megoldásban ismertetett módon
készítsük el az \(\displaystyle A_1,A_2,\ldots,A_{\lceil n/2\rceil}\) sorozatot úgy, hogy minden
\(\displaystyle i\le\lceil
n/2\rceil\) esetén \(\displaystyle {\cal P}\setminus\{A_1,\ldots,A_{i-1}\}\) konvex burka az
AiBC háromszög legyen.
elemű általános helyzetű ponthalmaz nem
tartalmaz n pontot, melyek konvex burka nem háromszög. Legyen
P konvex burka az ABC háromszög, és legyen
A1=A. Az első megoldásban ismertetett módon
készítsük el az \(\displaystyle A_1,A_2,\ldots,A_{\lceil n/2\rceil}\) sorozatot úgy, hogy minden
\(\displaystyle i\le\lceil
n/2\rceil\) esetén \(\displaystyle {\cal P}\setminus\{A_1,\ldots,A_{i-1}\}\) konvex burka az
AiBC háromszög legyen.
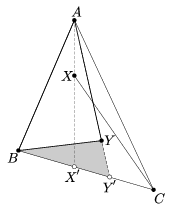
Rendezzük sorba az \(\displaystyle A_2,\ldots,A_{\lceil n/2\rceil}\) pontokat az
A-ból nézve pozitív irányban, és jelölje közülük a két szélsőt
X és Y. Az AX és AY egyenesek BC
szakasszal alkotott metszéspontját jelölje X' és Y'. Az
általánosság megszorítása nélkül feltehetjük, hogy a B,
X', Y', C pontok ebben a sorrendben követik
egymást a BC egyenesen. A BCX és BCY
háromszögek közül valamelyik tartalmazza a másikat. Ezek közül a
kisebbik, melyet lefed a BYY' és CXX' háromszögek
egyesítése, tartalmazza a \(\displaystyle {\cal P'}={\cal
P}\setminus\big\{A_1,A_2,\ldots,A_{\lceil n/2\rceil},B,C\big\}\)
legalább n-3 elemű ponthalmazt. Az általánosság megszorítása
nélkül feltehetjük, hogy P' pontjainak legalább a fele a
BYY' háromszögbe esik (ábra). Válasszunk ki ezek közül 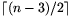 pontot, ezek halmazát jelölje
P''. Tekintsük végül a \(\displaystyle {\cal Q}={\cal
P}''\cup\big\{A_1,A_2,\ldots,A_{\lceil n/2\rceil},B\big\}\)
halmazt. Q-nak \(\displaystyle \big\lceil(n-3)/2\rceil+\lceil
n/2\big\rceil+1=n\) eleme van, és minden eleme az AY'B
háromszögbe, vagy annak határára esik. Ezért az A, Y,
B pontok a Q halmaz konvex burkán helyezkednek
el. A konvex buroknak tartalmaznia kell továbbá a P''
halmaznak legalább egy pontját is, ami ellentmond az indirekt
feltevésünknek.
pontot, ezek halmazát jelölje
P''. Tekintsük végül a \(\displaystyle {\cal Q}={\cal
P}''\cup\big\{A_1,A_2,\ldots,A_{\lceil n/2\rceil},B\big\}\)
halmazt. Q-nak \(\displaystyle \big\lceil(n-3)/2\rceil+\lceil
n/2\big\rceil+1=n\) eleme van, és minden eleme az AY'B
háromszögbe, vagy annak határára esik. Ezért az A, Y,
B pontok a Q halmaz konvex burkán helyezkednek
el. A konvex buroknak tartalmaznia kell továbbá a P''
halmaznak legalább egy pontját is, ami ellentmond az indirekt
feltevésünknek.
III. Megoldás. (Ez a megoldás Lippner Gábortól
származik.) Akárcsak az első megoldásban, most is feltehetjük, hogy a
pontok konvex burka egy ABC háromszög. Két olyan pontot, mely a
háromszög belsejében fekszik, kössünk össze egy piros, kék vagy zöld
színű szakasszal aszerint, hogy az általuk meghatározott egyenes a
háromszög három oldala közül melyiket nem metszi: az AB, a
BC vagy a CA oldalt. Jelölje rendre P, K
és Z azon pontok halmazát, melyekből indul ki piros, kék,
illetve zöld színű szakasz. Az n\(\displaystyle ge\)4 feltevés miatt az ABC
háromszög belsejében legalább 2 pont helyezkedik el, és ezért a
P\(\displaystyle cup\)K Z halmaz
megegyezik a háromszög belsejében lévő pontok halmazával, tehát
Z halmaz
megegyezik a háromszög belsejében lévő pontok halmazával, tehát 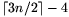 eleme van. Megmutatjuk, hogy a P,
K, Z halmazok valamelyikének az elemszáma legalább
n-2. Ennek igazolásához készítsük el a halmazok
Venn-diagrammját, ahol az egyes betűk a megfelelő részhalmazok
elemszámát jelölik.
eleme van. Megmutatjuk, hogy a P,
K, Z halmazok valamelyikének az elemszáma legalább
n-2. Ennek igazolásához készítsük el a halmazok
Venn-diagrammját, ahol az egyes betűk a megfelelő részhalmazok
elemszámát jelölik.
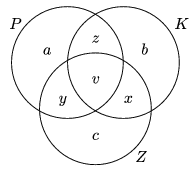
Ha mondjuk a\(\displaystyle ne\)0, akkor van olyan pont a háromszög belsejében, amelyet minden további ponttal piros színű szakasz köt össze, ekkor tehát
\(\displaystyle |P|=\lceil3n/2\rceil-4\ge n-2,\)
hiszen n\(\displaystyle ge\)4. Feltehetjük tehát, hogy
a=b=c=0. Ez azt jelenti, hogy |P K
K Y|=x+y+y+v. Ha most
|P|=y+z+v,
|K|=z+x+v és
|Z|=x+y+v mindegyike kisebb lenne, mint
n-2, akkor összegzés után a
Y|=x+y+y+v. Ha most
|P|=y+z+v,
|K|=z+x+v és
|Z|=x+y+v mindegyike kisebb lenne, mint
n-2, akkor összegzés után a
\(\displaystyle 3n-8\le2\big(\lceil3n/2\rceil-4\big)=2(x+y+z+v)\le|P|+|K|+|Z|\le3(n-3)=3n-9\)
egyenlőtlenséghez jutnánk, ami lehetetlen.
Valóban igaz tehát, hogy valamelyik halmaz elemszáma legalább n-2. Az általánosság megszorítása nélkül feltehetjük, hogy |P|\(\displaystyle ge\)n-2\(\displaystyle ge\)2. Tekintsük a P'=P\(\displaystyle cup\){A,B} legalább n elemű halmazt, ennek konvex burka tartalmazza az A és B csúcsokat. Legyen D\(\displaystyle in\)P, és tekintsük P-nek egy olyan E pontját, melyre a DE szakasz piros. Mivel a DE egyenes nem metszi az AB szakaszt, az E pont nem lehet az ABD háromszög belsejében. Ezért P' konvex burka nem lehet háromszög. Már csak annyit kell megjegyeznünk, hogy ekkor P'-ből kiválasztható egy n\(\displaystyle ge\)4 elemű részhalmaz, melynek konvex burka szintén nem háromszög.
2. Legyen k\(\displaystyle ge\)3 egész szám, \(\displaystyle \){k\choose3}">. Bizonyítandó, hogy ha ai, bi, ci (1\(\displaystyle le\)i\(\displaystyle le\)n) 3n darab különböző valós szám, akkor az ai+bi,ai+ci,bi+ci számok között legalább k+1 különböző szám található. Mutassuk meg, hogy \(\displaystyle n={k\choose3}\) esetén az állítás nem feltétlenül igaz.
I. Megoldás. Tegyük fel, hogy az állítás nem igaz, vagyis az ai+bi, ai+ci, bi+ci számok között legfeljebb k különböző szám található, ezek halmazát jelölje T. Világos, hogy minden 1\(\displaystyle le\)i\(\displaystyle le\)n esetén az ai+bi, ai+ci, bi+ci számok páronként különbözők, vagyis T-nek egy 3-elemű részhalmazát alkotják. Továbbá, ha ai+bi=x, ai+ci=y és bi+ci=z, akkor ai=(x+y-z)/2, bi=(x+z-y)/2 és ci=(y+z-x)/2. Az {x,y,z} halmaz ismeretében az {ai,bi,ci} halmaz tehát egyértelműen meghatározható. Minthogy
\(\displaystyle {|T|\choose3}\le{k\choose3} A második állítás bizonyításához tekintsük a
T={t1,t2,...,tk}
halmazt, ahol ti=4i. Legyen
\(\displaystyle n={k\choose3}\), és jelölje
T1,T2,...,Tn
a T halmaz 3-elemű részhalmazait. Ha
Ti={4u,4v,4w},
ahol 1\(\displaystyle le\)u<v<w\(\displaystyle le\)k egész számok, akkor legyen
ai=(4u+4v-4w)/2,
bi=(4u+4w-4v)/2
és
ci=(4v+4w-4u)/2,
ekkor nyilván
ai+bi,ai+ci,bi+ci vagy ai=cj
semmilyen i,j esetén nem állhat fenn, hiszen az
ai számok mind negatívak, míg a
bj, cj számok mind
pozitívak. Az sem lehet, hogy
bi=cj, hiszen a
bi számok mindegyike valamelyik
(22s-2,22s-1) alakú intervallumba
esik, míg a ci számok mindegyike valamelyik
(22s-1,22s) alakú intervallumba
esik, ahol 3\(\displaystyle le\)s\(\displaystyle le\)k egész szám.
Legyen most
Ti={4u,4v,4w}
és
Tj={4x,4y,4z},
ahol 1\(\displaystyle le\)u<v<w\(\displaystyle le\)k és 1\(\displaystyle le\)x<y<z 4v+4w-4u=4y+4z-4x.
Mivel
4w<4v+4w-4u<4w+1
és
4z<4y+4z-4x<4z+1,
ez csak úgy lehet, ha w=z, következésképpen
4v-4u=4y-4x. Itt
4v-1<4v-4u<4v
és
4y-1<4y-4x<4y,
ezért az egyenlőség csak úgy állhat fenn, ha v=y, és
ekkor szükségképpen u=x, i=j is
igaz. A ci számok tehát mind különbözők.
Ugyanilyen gondolatmenettel megállapíthatjuk azt is, hogy mind az
ai számok, mind a bi
számok különbözők, amivel a bizonyítás végére értünk.
II. Megoldás. A feladat első részére mutatunk egy másik
indoklást, ez Kiss Demetertől származik. Tegyük fel ismét, hogy
az állítással ellentétben a 3n összeg között legfeljebb
k különböző szám található. Ekkor ezek közül valamelyik,
jelöljük ezt a-val, legalább \(\displaystyle {3n\over k\){k-1\choose2}"> alkalommal fordul
elő. Ha valamilyen i-re az
ai+bi,
bi+ci és
ai+ci összegek közül
kettő is egyenlő lenne a-val, akkor az
ai, bi,
ci számok között lenne két megegyező. Az
általánosság megszorítása nélkül feltehetjük tehát, hogy minden \(\displaystyle 2\left({k-1\choose2}+1\right)\Big/(k-1\)k-2">
alkalommal fordul elő. Az előző okoskodáshoz hasonlóan tehát
feltehetjük, hogy minden 1\(\displaystyle le\)i\(\displaystyle le\)k-1 esetén az
ai+bi,
bi+ci és
ai+ci összegek közül
az egyik a-val, egy másik pedig b-vel egyenlő. A még
megmaradó k-1 összeg pedig már csak legfeljebb k-2
különböző értéket vehet fel, lesz tehát köztük kettő, amelyik
megegyezik. Ekkor azonban az ezekhez tartozó
ai, bi,
ci számhármasok is megegyeznek, mely
ellentmondás bizonyítja az állítást.
A továbbiakban a feladat második részére mutatunk több megoldást.
III. Megoldás. Tekintsük a
T={t1,t2,...,tk}
halmazt, ahol ti=3i. Legyen
{x,y,z} és {u,v,w} az
{1,2,...k} halmaz két 3-elemű részhalmaza. Az
I. megoldáshoz hasonlóan, annyit kell csak megmutatnunk, hogy ha
\(\displaystyle {3^x+3^y-3^z\over2}={3^u+3^v-3^w\over2},\)
akkor a két részhalmaz szükségképpen megegyezik, és
z=w. Valóban, ekkor
3x+3y+3w=3u+3v+3z=A. Ha
az A számot hármas számrendszerben írjuk fel, akkor annak 0-tól
különböző számjegyei között vagy három 1-es, vagy egy 1-es és egy 2-es
számjegy szerepel, hiszen x=y=w nem
lehetséges. A felírás egyértelműsége miatt az első esetben
{x,y,w} és {u,v,z} az
{1,2,...k} halmaznak ugyanaz a 3-elemű részhalmaza. Mivel
x,y\(\displaystyle ne\)z, ebből w=z, majd
{x,y}={u,v} is következik, ahogyan azt
bizonyítani kívántuk. A második esetben azt kapnánk, hogy
{x,y,w} és {u,v,z} az
{1,2,...k} halmaznak ugyanaz a 2-elemű részhalmaza. Mivel
x\(\displaystyle ne\)y, ez
meg kellene egyezzen az {x,y} halmazzal, ahonnan
z\(\displaystyle in\){x,y} következne, ami nem lehetséges.
IV. Megoldás. Ahogyan azt az eddigi megoldások is sugallják,
elegendő azt megmutatni, hogy minden k pozitív egész esetén
létezik egy olyan
Tk={t1,t2,...,tk}
halmaz, melyre
tx+ty+tz=tu+tv+tw
akkor és csak akkor teljesül, ha az x, y, z
számok valamilyen sorrendben megegyeznek az u, v,
w számokkal. Valóban, ekkor nem nehéz megmutatni, hogy a
(tx+ty-tz)/2
alakban felírható \(\displaystyle 3{k\choose3}\) szám (ahol {x,y,z} az
{1,2,...k} halmaz tetszőleges 3-elemű részhalmaza) mind
különböző.
Ha k=1 akkor a t1=1 választás nyilván
megfelelő. Elegendő megmutatni azt, hogy létezik olyan végtelen
t1,t2,...,ti,... sorozat,
hogy minden i\(\displaystyle ge\)2 esetén ti nem írható fel
r1t1+...+ri-1ti-1
alakban, ahol r1,...ri-1
racionális számok. Tegyük fel ugyanis, hogy létezik ilyen sorozat,
tekintsük a Tk halmazt, és tegyük fel, hogy
tx+ty+tz=tu+tv+tw
teljesül valamilyen 1\(\displaystyle le\)x,y,z,u,v,w Tegyük fel tehát, hogy k>1, és a
t1,...,tk-1 számokat már
meghatároztuk a fenti kívánalomnak megfelelően. Ekkor az
r1t1+...+rk-1tk-1
alakban felírható számok halmaza megszámlálhatóan végtelen, míg az
összes valós szám halmaza nem az, létezik tehát olyan
tk valós szám, mely nem írható fel
r1t1+...+rk-1tk-1
alakban. Ezért a kívánt tulajdonságú sorozat létezése azonnal
következik a teljes indukció elvéből.
Megjegyzések. 1. Az előző megoldásban nem konstruktív
módon igazoltuk egy alkalmas
t1,t2,...,ti,... sorozat
létezését. Megmutatható, hogy például a 2. Ahogyan azt Kocsis Albert Tihamér észrevette, a
feladat átalánosítható a következő módon. Legyenek k 3. Merőben más a helyzet, ha kéttagú összegeknél
maradunk. Világos, hogy ha k\(\displaystyle ge\)3 egész szám,  T. Ezért
elegendő megmutatni, hogy az
ai,bi,ci
(1\(\displaystyle le\)i
T. Ezért
elegendő megmutatni, hogy az
ai,bi,ci
(1\(\displaystyle le\)i n) számok mind
különbözők. ai=bj
n) számok mind
különbözők. ai=bj
 k egész
számok. Tegyük fel, hogy
ci=cj, ekkor
k egész
számok. Tegyük fel, hogy
ci=cj, ekkor
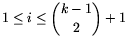 esetén az
ai+bi,
bi+ci és
ai+ci összegek közül
pontosan egy lesz a-val egyenlő. Az ezen összegek közül
fennmaradó \(\displaystyle 2\left({k-1\choose2}+1\right)\) összeg most már csak k-1
különböző értéket vehet fel, van tehát egy olyan érték, jelöljük ezt
b-vel, amely legalább
esetén az
ai+bi,
bi+ci és
ai+ci összegek közül
pontosan egy lesz a-val egyenlő. Az ezen összegek közül
fennmaradó \(\displaystyle 2\left({k-1\choose2}+1\right)\) összeg most már csak k-1
különböző értéket vehet fel, van tehát egy olyan érték, jelöljük ezt
b-vel, amely legalább
 k esetén. Legyen
i az x, y, z, u, v, w
indexek között előforduló legnagyobb szám. Ha most
ti nem ugyanannyiszor szerepelne az
egyenlőség két oldalán, akkor átrendezés után egy
ti=r1t1+...+ri-1ti-1
alakú egyenlőséghez jutnánk. Ezért i ugyanannyiszor szerepel az
x, y, z számok között, mint az u,
v, w számok között. Mindkét oldalról elhagyva a
ti-vel egyenlő tagokat, és az előbbi lépést
megismételve végül azt kapjuk, hogy az x, y, z
számok valamilyen sorrendben valóban megegyeznek az u,
v, w számokkal.
k esetén. Legyen
i az x, y, z, u, v, w
indexek között előforduló legnagyobb szám. Ha most
ti nem ugyanannyiszor szerepelne az
egyenlőség két oldalán, akkor átrendezés után egy
ti=r1t1+...+ri-1ti-1
alakú egyenlőséghez jutnánk. Ezért i ugyanannyiszor szerepel az
x, y, z számok között, mint az u,
v, w számok között. Mindkét oldalról elhagyva a
ti-vel egyenlő tagokat, és az előbbi lépést
megismételve végül azt kapjuk, hogy az x, y, z
számok valamilyen sorrendben valóban megegyeznek az u,
v, w számokkal.
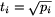 választással, ahol pi az i-edik
pozitív prímszámot jelöli, megfelelő sorozathoz jutunk. Ennek
bizonyítása azonban már túl messzire vezetne.
választással, ahol pi az i-edik
pozitív prímszámot jelöli, megfelelő sorozathoz jutunk. Ennek
bizonyítása azonban már túl messzire vezetne.
 t
t 3 egész számok,
\(\displaystyle \){k\choose
t}">. Ha
ai1,ai2,...,ait
(1\(\displaystyle le\)i
3 egész számok,
\(\displaystyle \){k\choose
t}">. Ha
ai1,ai2,...,ait
(1\(\displaystyle le\)i n) tn
különböző valós szám, akkor a \(\displaystyle \sum_{i=1}^ta_i-a_k\) (1
n) tn
különböző valós szám, akkor a \(\displaystyle \sum_{i=1}^ta_i-a_k\) (1 i
i n, 1
n, 1 k
k t) számok között
legalább k+1 különböző szám található,
t) számok között
legalább k+1 különböző szám található, 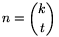 esetén pedig ez nem mindig van így. Ennek igazolását az olvasó könnyen
elvégezheti, nincsen szükség hozzá alapvetően új gondolatra.
esetén pedig ez nem mindig van így. Ennek igazolását az olvasó könnyen
elvégezheti, nincsen szükség hozzá alapvetően új gondolatra.
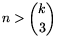 ,
és ai, bi,
ci, di (1
,
és ai, bi,
ci, di (1 i
i n) 4n
különböző valós szám, akkor az
ai+bi,
ai+ci,
ai+di,
bi+ci,
bi+di,
ci+di összegek
között legalább k+1 különböző szám található. Meglepő módon ez
az állítás lényegesen nem javítható. Érdemes elgondolkozni a következő
feladaton: minden k\(\displaystyle ge\)3 egész számra létezik \(\displaystyle 4{k\choose3}\) különböző valós szám,
ai, bi,
ci, di
n) 4n
különböző valós szám, akkor az
ai+bi,
ai+ci,
ai+di,
bi+ci,
bi+di,
ci+di összegek
között legalább k+1 különböző szám található. Meglepő módon ez
az állítás lényegesen nem javítható. Érdemes elgondolkozni a következő
feladaton: minden k\(\displaystyle ge\)3 egész számra létezik \(\displaystyle 4{k\choose3}\) különböző valós szám,
ai, bi,
ci, di 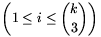 úgy, hogy az
ai+bi,
ai+ci,
ai+di,
bi+ci,
bi+di,
ci+di összegek
között legfeljebb 2k különböző szám található.
úgy, hogy az
ai+bi,
ai+ci,
ai+di,
bi+ci,
bi+di,
ci+di összegek
között legfeljebb 2k különböző szám található.
3. Egy négyzetrácsban tekintsünk egy adott háromszöghöz hasonló legkisebb területű rácsháromszöget. Bizonyítsuk, hogy körülírt körének középpontja nem rácspont.
I. Megoldás. (Gerencsér Balázs megoldása.) Tekintsünk egy olyan rácsháromszöget, melynek körülírt körének középpontja is rácspont. Az általánosság megszorítása nélkül feltehetjük, hogy az egyik csúcspont (A) az origó. Legyenek a másik két csúcs koordinátái B=(a,b) és C=(c,d), a körülírt kör középpontjáé pedig O=(x,y).
Az OA és OB szakaszok egyenlőségéből a Pitagorasz tétel alapján nyerjük, hogy x2+y2=(a-x)2+(b-y)2, ahonnan leolvasható, hogy a2+b2, és így a+b és a-b is páros számok. Hasonlóképpen kapjuk, hogy c+d és c-d is páros számok.
Tekintsük most az A1B1C1 rácsháromszöget, ahol
A1=A, 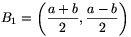 és
és 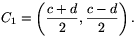
Ebben a háromszögben
\(\displaystyle \overline{A_1B_1}^2=\left({a+b\over2}\right)^2+\left({a-b\over2}\right)^2={a^2+b^2\over2}={\overline{AB}^2\over2},\)
\(\displaystyle \overline{A_1C_1}^2=\left({c+d\over2}\right)^2+\left({c-d\over2}\right)^2={c^2+d^2\over2}={\overline{AC}^2\over2}\)
és
\(\displaystyle \overline{B_1C_1}^2=\left({a+b-c-d\over2}\right)^2+\left({a-b-c+d\over2}\right)^2={{(a-c)}^2+{(b-d)}^2\over2}={\overline{BC}^2\over2}.\)
Az A1B1C1 háromszög oldalai tehát rendre megegyeznek az ABC háromszög megfelelő oldalainak \(\displaystyle \sqrt{2}\)-ed részével, a két háromszög ennek megfelelően hasonló. Ilyen módon találtunk egy, az ABC háromszöghöz hasonló, annál kisebb területű rácsháromszöget. Ez bizonyítja az állítást.
II. Megoldás. Tegyük fel, hogy egy H rácsháromszög körülírt körének O középpontja is rácspont. Legyenek az egyik oldalvektor koordinátái (x,y), az O pontból a szóban forgó oldal csúcsaiba mutató vektorok koordinátái pedig (a,b), illetve (c,d). Ekkor a, b, c, d, x, y egész számok, melyekre a Pitagorasz tétel alapján
x2+y2=(a-c)2+(b-d)2=(a2+b2)+(c2+d2)-2(ac+bd)
teljesül. Mivel a2+b2=c2+d2 (a körülírt kör sugarának négyzete), x2+y2, és így (x+y)2 is páros szám. Következésképpen x+y és x-y is páros számok.
Ha az (x,y) vektort az origó körül 45o-os
szöggel elforgatjuk pozitív irányba, akkor az 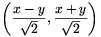 vektort
kapjuk, ezt \(\displaystyle {1\over\sqrt{2}}\) arányban nagyítva pedig az
vektort
kapjuk, ezt \(\displaystyle {1\over\sqrt{2}}\) arányban nagyítva pedig az 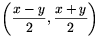 vektorhoz jutunk,
melynek mindkét koordinátája egész szám.
vektorhoz jutunk,
melynek mindkét koordinátája egész szám.
Megállapíthatjuk tehát, hogy H-t bármely csúcsa körüli 45o-os szöggel történő \(\displaystyle {1\over\sqrt{2}}\) arányú forgatva nyújtás egy hozzá hasonló, ám nála kisebb rácsháromszögbe viszi. Ez bizonyítja az állítást.
Megjegyzés. Bontsunk fel egy húrsokszöget valamely csúcsából induló átlóinak segítségével háromszögekre. Mivel ezen háromszögek körülírt köreinek ugyanaz a középpontja, ez a megoldás mutatja azt is, hogy a feladat állítása háromszög helyett tetszőleges húrsokszögre is igaz.
Károlyi Gyula
Jelentés a 2001. évi Kürschák József Matematikai Tanulóversenyről

