Szabó Péter Gábor: Sangaku, matematikai fatáblák japán templomokban

1. Bevezetés

Az Edo korszak (1603-1867) ideje alatt Japán el volt zárva a nyugati világtól. Ebben az időszakban tanult emberek (társadalmi helyzetüktől függetlenül) számos geometriai összefüggést fedeztek fel. Az eredményeket fatáblára rajzolták, szépen kiszínezték és elhelyezték egy-egy sintoista szentélyben vagy buddhista templomban, általában a tetőről lelógatva. Az ilyen táblát hívják sangakunak, amely matematikai táblát jelent japánul. A fatáblák közül több van, amely olyan igényesen lett elkészítve, hogy művészi alkotásnak is tekinthető. Sok ügyes geométer ajánlott sangakut köszönetként az égieknek egy-egy újabb tétel felfedezéséért. A bizonyításokat ritkán közölték, a problémák ezért kihívások lehettek mások számára. Egy sangakun rendszerint több feladat is szerepelt. (1. ábra.)

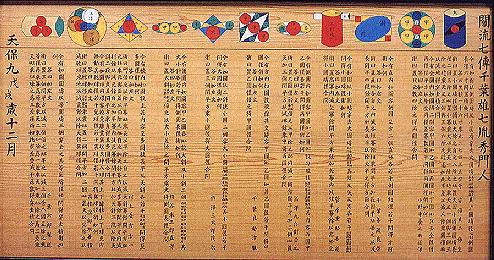
1. ábra

A történelem folyamán számos sangaku elveszett, de így is több mint 800 megmaradt és azok ma is kellemes perceket szerezhetnek a geometria kedvelőinek. Az, hogy most kedvünkre nézelődhetünk a múlt eme relikviái közt, jórészt egy japán középiskolai tanárnak, Hidetoshi Fukagawanak köszönhető. Fukagawa afféle tudós tanár, aki Ph.D. fokozatot is szerzett matematikából. Néhány évtizeddel ezelőtt elhatározta, hogy tanulmányozni fogja a japán matematikatörténetet, hogy a tapasztalatok birtokában eredményesebben taníthassa a diákokat. Egy régi könyvtári könyvben talált említést bizonyos matematikai fatáblákról, amelyekről korábban sohasem hallott. Ezt követően bejárta Japánt, hogy összegyűjtse nemcsak a sangakuról maradt emlékeket, hanem a régi japán matematika (Wasan) más eredményeit is. A munka nem volt egyszerű, hiszen ahhoz, hogy a fennmaradt szövegeket el tudja olvasni, tanulmányoznia kellett a japán nyelv archaikus változatát, a kambunt is, amely az Edo korban a tudomány nyelve volt. Az összegyűjtött anyagot később több helyen is publikálta. 1989-ben jelent meg először angol nyelven gyűjteményes kötet a sangakuról, amelyet H. Fukagawa és D. Pedoe írtak [1,4].

2. Sangaku feladatok

A továbbiakban egy kis ízelítőt adunk a sangaku problémákból. Az itt közölt feladatok mind geometriai problémák lesznek, de megjegyezzük, hogy fennmaradtak olyan fatáblák is, amelyen számelméleti kérdéseket, nevezetesen diophantoszi egyenleteket tárgyaltak. A sangaku problémák különböző nehézségűek. Vannak viszonylag könnyen megoldható feladatok, de akadnak olyanok is, amelyek elegáns megoldása komoly teljesítménynek számít. Az itt közölt feladatok megoldhatók pusztán elemi geometriai megfontolásokkal.

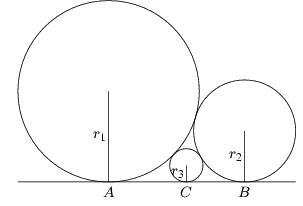
1. feladat (1824, Gumma prefektúra). Milyen összefüggés van a 2. ábrán látható körök sugara között, ahol a három kör és az egyenes kölcsönösen érintik egymást? (A válasz: .)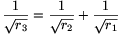

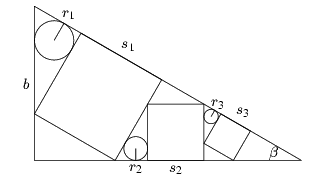2. ábra	3. ábra

2. feladat (1913, Mijagi prefektúra). Egy derékszögű háromszögbe négyzeteket rajzoltunk a 3. ábrán látható módon. Milyen összefüggés van a keletkező háromszögekbe rajzolt körök r₁, r₂ és r₃ sugara között? (A válasz: .)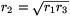

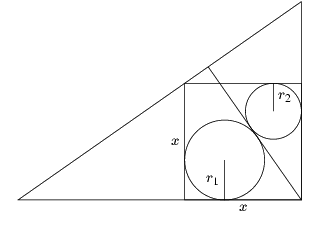
3. feladat (1811, Gumma prefektúra). Egy derékszögű háromszögbe négyzetet rajzoltunk, amelynek két oldala a befogókon fekszik. Az átfogóhoz tartozó magasság a négyzetet két részre osztja, amely alakzatokba egy-egy kört írtunk a 4. ábrán látható módon. Határozzuk meg a négyzet x oldalhosszúságát a két kör r₁ és r₂ sugarának függvényében! (A válasz: \(\displaystyle x=r_1+r_2+\sqrt{r_1^2+r_2^2}\).)

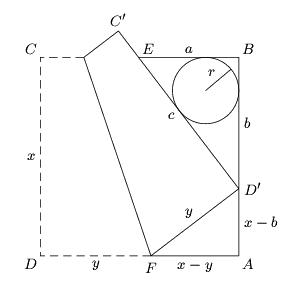4. ábra	5. ábra

4. feladat (1815, Shiga prefektúra). Egy négyzet alakú ABCD papírlapot félbehajtottunk az 5. ábrán látható módon úgy, hogy a D csúcs az AB oldalra essen. Bizonyítsuk be, hogy a BED' háromszögbe írt kör sugarának hossza megegyezik a C'E szakasz hosszúságával!

5. feladat (1872, Szaitama prefektúra). Milyen összefüggés van a 6. ábrán látható nagy kör R és a 6 egybevágó kis kör r sugara között? (A válasz: R=4r.)

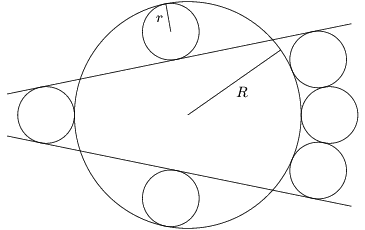6. ábra

A feladatok megoldásai és további információ található a szerző honlapján a http://www.inf.u-szeged.hu/~pszabo/Sangaku.html címen.

Ezúton köszönöm Dr. Csendes Tibornak, a Szegedi Tudományegyetem docensének, hogy értékes megjegyzéseivel segítette a dolgozat elkészítését és Dr. Tarnai Tibornak, a Budapesti Műszaki és Gazdaságtudományi Egyetem egyetemi tanárának, hogy elküldte egy, a témához kapcsolódó cikkét.

Irodalomjegyzék

[1.] H. Fukagawa and D. Pedoe, Japanese temple geometry problems - Sangaku, Charles Babbage Research Centre, Winnipeg, Canada, 1989.

[2.] Hiroshi Okumura, Variations of the ratio 1:4, Mathematics and Informatics Quarterly, 3:162-166, 1993.

[3] Y. Mikami, The development of mathematics in China and Japan, Chelsea Publishing Company, New York, 1914.

[4] Tony Rothman, Japanese temple geometry, Scientific American, 5, 1998. Elérhető a http://www.sciam.com/1998/0598issue/0598rothman.html címen is.

[5] D. E. Smith and Y. Mikami, A history of Japanese mathematics, Open Court Publishing Company, Chicago, 1914.

[6] T. Tarnai, Packing of equal circles in a circle, megjelent a Structural Morphology: Toward the New Millennium kötetben, The University of Nottingham, Nottingham, UK, 217-224, 1997.

[7] I. Yamamoto, The Sangaku in Hyogo, 1967 (magánkiadás japánul).

[8] Y. Yasutomi, The Sangaku in Iwate, Seijisya, Tokyo, 1987 (japánul).