KöMaL Problems in Physics, January 2006
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on February 13, 2006. |
M. 266. Make a ``magnetic pendulum'' using a piece of magnet and a piece of iron. Fix one of them to the table while the other is swinging above it. Examine the motion of the bob of the pendulum as a function of the initial deflection angle and the distance between the bodies at the equilibrium position.
(6 pont)
 |
Problems with sign 'P'Deadline expired on February 13, 2006. |
P. 3854. An hour-glass is placed to one of the pans of a pair of scales which is balanced while the sand trickles down. Does the equilibrium of the scales change when all the sand is in the lower chamber?
(3 pont)
P. 3855. Estimate whether the rotation of the Earth could be stopped if all the people living on the Earth lined up along the equator, and marched in the appropriate direction.
(3 pont)
P. 3856. The air pressure inside the 8 l bell-jar of an air pump at 20 oC is 100 Pa. Are there as many oxygen molecules left in the jar as the number of people living on the Earth?
(4 pont)
P. 3857. Thomas is long-sighted. He is able to see clearly only those objects which are at least 1 m away. Find the power of the glasses through which he is able to read a book 25 cm away from his eyes.
(3 pont)
P. 3858. We would like to increase the length of a 160 cm long copper rod of cross section 4 mm2 by 1 mm. What is the energy absorbed by the rod if
a) the rod is stretched;
b) the rod is heated?
(4 pont)
P. 3859. The angle of elevation of an inclined plane of length L is  . The coefficient of friction on the top half of the plane is
. The coefficient of friction on the top half of the plane is 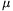 1 and on the bottom part
1 and on the bottom part 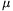 2. At the top of the plane a plate of length l<L/2 is released. (The contact between the surface of the plate and the slope is uniform.) Under what conditions does the plate stop exactly when the front of the plate reaches the bottom of the slope.
2. At the top of the plane a plate of length l<L/2 is released. (The contact between the surface of the plate and the slope is uniform.) Under what conditions does the plate stop exactly when the front of the plate reaches the bottom of the slope.
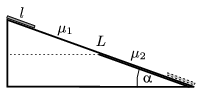
(5 pont)
P. 3860. There is a semi-cylinder of radius R and mass M at rest on a horizontal table. On the top of the semi-cylinder there is a small cube of mass m=M/2. What is the force exerted by the sliding cube on the semi-cylinder in the position of
 =30o if a) the semi-cylinder is fixed?
=30o if a) the semi-cylinder is fixed?
b) if the semi-cylinder can slide along the table without friction?
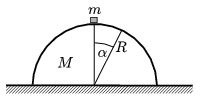
(5 pont)
P. 3861. The internal part of a long-necked vase is a vertical cylinder, the diameter of its base is 3 cm and its volume is 2 dl. The vase is filled with water such that the air column above the water amplifies the sound of a vibrating tuning fork placed above the vase. Interestingly if the water from this vase is poured into another long-necked vase, the air above the water again amplifies the sound of the tuning fork. The internal part of this vase is a cylinder with base diameter 3 cm, and volume 3 dl. The bottoms of both vases are 1.7 cm thick, the speed of sound in air is 342 m/s, and the frequency of the tuning fork is smaller than 1 kHz.
a) Find the heights of the vases.
b) Find the volume of the water that was poured into the vases.
c) What is the frequency of the tuning fork?
(4 pont)
P. 3862. A ray of light enters into a spherical water drop. After refraction it is reflected at the internal boundary of the drop, and then it leaves the drop at another point. a) Prove (numerically) that if the angle of incidence is greater than a certain ``critical'' angle, then there exists another ray parallel to the original ray, and after leaving the drop the two rays remain also parallel. Find this ``critical'' angle. b) What is the distance between the two parallel incident rays if the refractive index of water is n=4/3, the angle of incidence of one of the rays is  =45o and the diameter of the water drop is 1 mm.
=45o and the diameter of the water drop is 1 mm.
(5 pont)
P. 3863. Photons collide with electrons of negligible speed. The energy of the photons is equal to the rest energy of the electrons. After the collision one of the electrons moves such that the angle between the original velocity of the photon and the velocity of the electron is 45o. Find the speed of this electron.
(5 pont)
Upload your solutions above.
