A KöMaL 2006. februári informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2006. március 16-án LEJÁRT. |
I. 124. Írjunk programot az ax+by=c alakú diophantoszi egyenletek megoldására. A program a standard bemeneten kapja a legfeljebb 4-jegyű a, b, c, egész számokat egy sorban, szóközzel elválasztva. A program írja ki az egész megoldásokat paraméteres alakban, szintén egy sorban, a példákban látható formátumban. Ha nincs megoldás, akkor írja ki azt, hogy ,,nincs megoldás''.
Példák:

Beküldendő a program forráskódja (i124.pas, i124.cpp, ...).
(10 pont)
I. 125. Készítsünk LATeX dokumentumot, ami a Ceva- és a Menelaosz-tételek kimondását tartalmazza. A szöveg elején szerepeljen a KöMaL megoldásoknál megszokott fejléc (a feladat száma, név, város, osztály, iskola, e-mail cím). Mindkét tételhez készítsünk ábrát EPS formátumban, és az epsfig csomag segítségével illesszük be a dokumentumba.
Az ékezetes magyar betűk kódolásához használjuk az inputenc csomagot.
Beküldendő a dokumentum LATeX forrása (i125.tex), valamint az EPS formátumú ábrák.
(10 pont)
I. 126. Készítsünk OpenOffice vagy Excel táblázatot a következő tulajdonságokkal. A felhasználó az első oszlopba beírhat legfeljebb 100 valós számot. A táblázat ezután automatikusan kiválasztja közülük az átlagnál kisebbeket, és ezeket a második oszlopban sorolja fel, az eredeti sorrendjüket megtartva. A második oszlopból is kiválasztja az átlag alattiakat, és ezeket a harmadik oszlopba gyűjti. Az eljárást addig folytatja, amíg a számok elfogynak.
Példa:
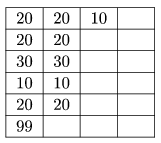
Beküldendő a táblázat (i126.sxc, i126.xls).
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2006. március 16-án LEJÁRT. |
S. 15. Írjunk programot Sam Lloyd híres tologatós játékának -- pontosabban a 3×3-as változatának -- kirakására. Egy 3×3-as, négyzet alakú dobozban 8 kis kocka van, megszámozva 1-től 8-ig, egy hely pedig üresen marad. Egy lépés abból áll, hogy valamelyik szomszédos kockát az üres helyre toljuk. Azt kell elérnünk, hogy az első sorban (balról jobbra) az 1, 2, 3-as, a második sorban a 4, 5, 6-os, a legalsó sorban a 7, 8-as kockák legyenek, az üres hely pedig a jobb alsó sarokban legyen.
A program a standard bemenetről olvassa be a kiinduló állapotot. Az állapot leírása három sorból fog állni soronként három, szóközökkel elválasztott számmal. Az üres mezőt a 0 jelenti.
A program keresse meg a legrövidebb (a lehető legkevesebb lépésből álló) megoldást és írja ki a standard kimenetre. Ha több legrövidebb megoldás van, akkor bármelyiket kiírhatja. A lépéseket az éppen arrébb tolt kockák számával kódoljuk. A számjegyeket egyetlen sorba írjuk, közvetlenül egymás után. Ha a feladatnak nincs megoldása, akkor írjuk ki azt, hogy ,,nincs megoldás''.
Példák:

Beküldendő a program forráskódja (s15.pas, s15.cpp, ...).
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

