A KöMaL 2006. márciusi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2006. április 10-én LEJÁRT. |
K. 79. Robi robot egy szobába van bezárva. Elindul egyenesen és megy, amíg falba nem ütközik. (Egy szobának csak a külső határvonal mentén lehetnek falai.) Ekkor jobbra fordul, és megy tovább. Ha nem tud jobbra fordulni, mert falba ütközne, balra fordul, és megy tovább. Ha nem tud sem jobbra, sem balra fordulni, akkor kikapcsolja magát.
Az 1. ábrán olyan szoba látható, melyben ha az 1-gyel jelölt helyről indul Robi, akkor miután körbejárja a szobát, oda is érkezik vissza, és ott leáll. A 2. ábrán olyan szoba látható, amelyben akár az 1-es, akár a 2-es helyről indul a robot, mindig a kiindulási helyre ér vissza, és ott leáll. A 3. ábrán az 1-es helyről a 2-esbe jut Robi, és ott leáll, míg a 2-esről az 1-esbe jut, és ott leáll. (Az ábrákon jelölt négyzetrács csak a tájékozódást segíti.)
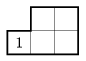
1. ábra
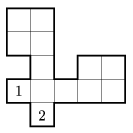
2. ábra
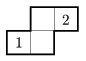
3. ábra
Rajzoljunk olyan szobát, ahol 4 kiindulási hely van: az 1-esből a 2-esbe jut, és ott leáll; a 2-esből a 3-asba jut, és ott leáll; a 3-asból az 1-esbe jut, és ott leáll; a 4-esből indulva ugyanoda érkezik vissza, és ott leáll.
(6 pont)
K. 80. A poliminók a dominók mintájára épülnek fel: kis négyzetekből állnak, melyek mindig teljes oldallal csatlakoznak egymáshoz. Egy P poliminó ,,határoló-számának'' azt a számot nevezzük, ahány különböző módon átfedés nélkül körülhatárolhatjuk a P egybevágó példányaival (minden éléhez csatlakoznia kell egy határoló poliminónak; a poliminót alkotó kis négyzeteknek teljes oldalukkal kell egy másik ilyen négyzethez csatlakozni). Például a kereszt alakzat határoló-száma 2, mert a következő két módon lehet körbehatárolni (a tükrözéssel egymásba vihető körülhatárolások is különbözőnek számítanak).
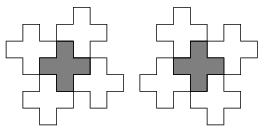
Adjuk meg a 3×3-as (vagyis 9 kis négyzetből álló) négyzet határoló-számát.
(6 pont)
K. 81. Hány darab olyan ABAABA alakú hatjegyű szám van, amely pontosan négy prímszám szorzatára bontható?
(6 pont)
K. 82. Van két, nem feltétlenül azonos méretű játékkockánk, melyek éleinek hossza egész szám. Egymásra tesszük ezeket úgy, hogy a felül levő kocka teljes lapjával érintkezzék az alul levő kocka egyik lapjával. Az így kapott test térfogatának mérőszáma megegyezik a felszínének a mérőszámával. Mekkorák az eredeti kockák élei?
(6 pont)
K. 83. Adott a síkon egy konvex hatszög, és a belsejében négy különböző pont úgy, hogy a hatszög csúcsai és az adott négy pont közül semelyik három nincs egy egyenesen. Vágjuk szét a hatszöget olyan háromszögekre, amelyek csúcsai a hatszög csúcsai és az adott négy pont közül valók (mind a 10 pontot fel kell használnunk). Mutassuk meg, hogy mindig 12 darab háromszöget kapunk.
(6 pont)
K. 84. Lehet-e egy négyzetszám jegyeinek az összege 2006?
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2006. április 18-án LEJÁRT. |
C. 845. Április elsején egy osztályban az algebrai átalakításokat gyakorolták matematikaórán. A feladat szerint egyszerűbb alakra kellett hozni az
törtet. Ági (aki az osztály legjobbja matematikából) vicces kedvében volt, ezért azt mondta, hogy ha a nevező nem nulla, akkor ,,egyszerűsítsünk'' a hármas kitevőkkel, vagyis az eredmény
Döntsük el, hogy jó-e a végeredmény.
(5 pont)
C. 846. Hányféle sorrendben alkothatnak a 0, 1, 2, 3, 4, 5, 6 számjegyek néggyel osztható hétjegyű számot? (A szám nem kezdődhet 0-val.)
(5 pont)
C. 847. Adjunk meg olyan egyenest, amely az ,,egyiptomi'' háromszög (oldalai: 3, 4, 5) kerületét és területét is felezi.
(5 pont)
C. 848. Határozzuk meg a kifejezés legkisebb és legnagyobb értékét.
(5 pont)
C. 849. Mekkora értéke, ha
?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2006. április 18-án LEJÁRT. |
B. 3892. A Piramis bank elnöke a kertvárosból jár be a munkahelyére dolgozni. Hétköznapokon egy sofőr jön érte, aki minden nap ugyanabban az időpontban indul a banktól, felveszi az elnököt, és pontosan nyitásra megérkeznek. Egyik reggel a sofőr telefonált, hogy valami baj van az autóval, ezért valószínűleg késni fog. Az elnök emiatt a szokottnál egy órával korábban, gyalog indult munkába. A sofőr közben megjavította az autót, és mégis el tudott indulni a szokásos időpontban, így útközben találkozott a bankárral. Felvette, és nyitás előtt 20 perccel érkeztek a bankhoz.
Mennyi ideig sétált a bankár? (Feltehetjük, hogy az autó sebessége állandó, és az utas felvétele nem jár időveszteséggel.)
Arany Dániel verseny, 2005--2006
(3 pont)
B. 3893. Oldjuk meg a valós számok halmazán az (x2+y2)3=(x3-y3)2 egyenletet.
Arany Dániel verseny, 2001--2002
(3 pont)
B. 3894. Az ABCD trapéz AB és CD szárainak egyenesei az M pontban metszik egymást. Az M-en átmenő e egyenes AD egyenesét az A-tól és D-től különböző E pontban, BC egyenesét pedig F-ben metszi. Az ABFE és a CDEF trapézok mindegyikében megszerkesztjük az átlók metszéspontját, jelölje ezeket P és Q. Mutassuk meg, hogy PQ párhuzamos a trapézok alapjaival.
(3 pont)
B. 3895. Egy négyzet alapú egyenes hasáb élei a=b=8, c=27 egység. Vágjuk szét a hasábot négy olyan részre, melyekből kockát lehet összerakni.
Javasolta: Lorántfy László
(5 pont)
B. 3896. Tekintsük egy hegyesszögű, nem egyenlő szárú háromszög magasság-egyeneseinek az oldalfelező merőlegesekkel alkotott metszéspontjait. Bizonyítsuk be, hogy e pontok két, egymással egybevágó, az eredeti háromszöghöz hasonló háromszöget határoznak meg.
Javasolta: Bodnár János
(4 pont)
B. 3897. Milyen n-re választható meg az változók értéke a {+1;-1} halmazból úgy, hogy
teljesüljön?
(4 pont)
B. 3898. Ismert, hogy egy tetszőleges tetraéder szemközti éleinek felezőpontjait összekötő szakaszok egy ponton mennek át. Ki lehet-e választani egy tetraéder minden élének egy harmadolópontját úgy, hogy a szemközti élekről választott harmadolópontokat összekötő szakaszok egy ponton menjenek át?
(3 pont)
B. 3899. Lehet-e négy egymást követő pozitív egész szám szorzata köbszám?
(5 pont)
B. 3900. Határozzuk meg azokat az (a1;a2) pozitív egész számpárokat, amelyekre az (n
 1) rekurzióval definiált sorozat periodikus.
1) rekurzióval definiált sorozat periodikus.
(5 pont)
B. 3901. Mi azon pontok mértani helye a síkban, amelyekből egy adott parabolához egymással 30o-os szöget bezáró érintők húzhatók?
(5 pont)
 |
A-jelű feladatokA beküldési határidő 2006. április 18-án LEJÁRT. |
A. 395. Legyen 1<a<2 valós szám.
(a) Mutassuk meg, hogy pontosan egy olyan x1,x2,... sorozat létezik, amelynek pozitív egészek az elemei és tetszőleges i esetén xi+1 xi2 és
xi2 és
(b) Bizonyítsuk be, hogy az xi+1>xi2 egyenlőtlenség akkor és csak akkor teljesül végtelen sok i indexre, ha a irracionális.
(5 pont)
A. 396. Az és a
halmazrendszer elemei legfeljebb n-elemű halmazok, ahol n adott pozitív egész. Tudjuk, hogy tetszőleges F véges halmazhoz létezik olyan
és
, amelyekre X
 Y
Y F=Ø. Bizonyítsuk be, hogy létezik olyan
F=Ø. Bizonyítsuk be, hogy létezik olyan és
is, amelyekre X
 Y=Ø.
Y=Ø.
(5 pont)
A. 397. Adott a síkon n egységkör (n 3), a középpontjaik O1,O2,...,On. A sík bármelyik egyenese legfeljebb két kört metsz. Igazoljuk, hogy
3), a középpontjaik O1,O2,...,On. A sík bármelyik egyenese legfeljebb két kört metsz. Igazoljuk, hogy
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

