A KöMaL 2007. októberi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2007. november 15-én LEJÁRT. |
I. 166. Készítsünk táblázatkezelő segítségével - a hátsó belső borítón láthatóhoz hasonló - véletlenszerű, de azért valódinak tűnő domborzati képet. A felszín rajzát diagramként egy munkalap 40×40-es cellatartományának 0 és 10 közötti magasságadatai alapján hozzuk létre. Az adatokat tartalmazó munkalapon az adatok alatt helyezzünk el egy parancsgombot, amelynek megnyomásakor a táblázatkezelő az adatokat újra létrehozza, tehát új felszínt készít. A felszín képét az adatok és a gomb alatt egy diagramon jelenítsük meg.
Beküldendő a táblázatkezelő munkafüzet (i166.xls, i166.ods, ...), illetve egy rövid dokumentáció (i166.txt, i166.pdf, ...) amelyben szerepel a megoldáshoz alkalmazott táblázatkezelő neve, verziószáma, valamint a megoldás rövid leírása.
(10 pont)
I. 167. Bolondos Bolha a következő mutatványra képes: egy vonalzó egész centimétereket jelző számain ugrál 0-tól 7-ig, a következő algoritmus szerint: másodpercenként átugrik arra a számra, mely a mostani helyén és az előző helyén lévő szám összegének 8-cal képzett osztási maradéka.
A bolha olyan kicsi, hogy nem látjuk, csak azt tudjuk, hogy most is a vonalzón ugrál. Szeretnénk visszatenni a dobozába, ezért minden másodpercben az egyik lehetséges helyéről megpróbálhatjuk elfogni.
Adjunk meg egy olyan minél rövidebb, de maximum 30 hosszú számsorozatot, mely alapján másodpercenként sorban végigpróbálva a számoknak megfelelő helyeket végére biztosan elkapjuk a bolhát. A számsor hosszától is függ a megoldásra kapott pontszám. A számsorozat ellenőrzéséhez letölthető a www.komal.hu honlapról a feladathoz egy Excel táblázat.
A problémát tetszőleges eszközzel meg lehet oldani: programírás, táblázat, ...
Beküldendő a számsorozat, lehetőség szerint a letölthető táblázatban (bolha.zip) tömörítve, illetve a megoldás menete néhány mondatban (i167.txt, i167.pdf, ...).
(10 pont)
I. 168. Egy téglalap alakú teremben három ,,drót nélküli'' (WiFi) jeladót helyeztünk el, ezek segítségével szeretnénk az ott dolgozó munkatársak számítógépeit hálózatba kötni. Tételezzük föl, hogy a jeladók erőssége a jeladótól vett távolsággal négyzetes arányban csökken, és a dolgozók számítógépe automatikusan ahhoz a jeladóhoz kapcsolódik, amelyiktől a legerősebb jelet érzékeli. Az egyszerűség kedvéért a terem mindig lefedhető 1 méter oldalhosszúságú négyzetekkel. A jeladók és a számítógépek mindegyike valamelyik így kapott mező belsejében van. Bármely két mező közötti távolságot úgy kapjuk meg, hogy megszámoljuk, legkevesebb hány mező érintésével lehet egyikből a másikba eljutni. Egy mező így önmagától 1 távolságra van. Az így kiszámított jelerősséget egész számra kerekítjük.
Például egy 4.3 négyzetméteres helyiségben, a (4;3) mezőben elhelyezett 90-es jelerősségű adó, az (1;1) mezőben levő 70-es jelerősségű adó, és az (1;3) mezőben levő 60-as jelerősségű adó esetén az alábbi ,,lefedettségi'' táblázatot kapjuk:
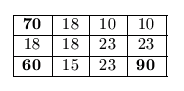
Azaz a (4;3)-as mezőn belül a jelerősség 90, mivel a távolság itt 1 egység. A vele szomszédos mezőkben (mivel azok távolsága tőle 2 egység) a jelerősség , ami kerekítve 23.
Készítsünk programot, amely tetszőleges, legfeljebb 25×25-ös teremre elkészíti a fenti táblázatot. A program a felhasználótól kérje be a terem méreteit, majd a három sugárzó koordinátáit és jelerősségeit. Az elkészült táblázatban minden szám egészre kerekítve, 3 karakter helyen jelenjen meg, és azt a program írja soronként a standard kimenetre.
Beküldendő a program forráskódja (i168.pas, i168.cpp, ...), a megoldás rövid dokumentációja (i168.txt, i168.pdf, ...) valamint a megoldáskor alkalmazott fordítóprogram neve és verziószáma (pl. Free Pascal 2.0, Borland C++ 3.1, ...).
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2007. november 15-én LEJÁRT. |
S. 29. Tavaly szeptemberben már találkozhattunk a Sudoku nevű játékkal (I. 136.), a mostani feladat is ehhez kapcsolódik. A játék megoldása során egy 9×9-es táblázatot kell kitöltenünk 1 és 9 közötti számokkal úgy, hogy minden sorban, oszlopban és 3×3-as kis négyzetben csak egyszer fordulhat elő minden egyes számjegy.
Készítsünk az alábbiak szerint működő programot, amely egy részben kitöltött táblázatot egészít ki:
- ha a megoldás egyértelmű, akkor a kimenet 9×9 karakter sorokra tördelve, a teljes kitöltött táblázat;
- ha a megoldás nem egyértelmű, akkor kiírandó egy lehetséges megoldás (9×9 karakter), a 10. sorban pedig ``A megoldas nem egyertelmu'' szöveg;
- ha nincs megoldás, akkor a kimenet egyetlen sora a ``Nincs megoldas'' szöveg.
A program bemenete a parancssor első argumentumaként kapott szöveges állomány, amely 9 sort tartalmaz. Ebben találhatók a számjegyek, illetve a hiányzó számjegyek helyén egy pont. Az eredmény a standard kimeneten jelenjen meg.
Beküldendő a program forráskódja (s29.pas, s29.cpp, ...), a megoldás rövid dokumentációja (s29.txt, s29.pdf, ...) valamint a megoldáskor alkalmazott fordítóprogram neve és verziószáma (pl. Free Pascal 2.0, Borland C++ 3.1, ...).
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

