KöMaL Problems in Mathematics, October 2007
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on November 10, 2007. |
K. 133. How many five-digit numbers are there in which the sum of the digits equals the sum of the square of the digits?
(6 pont)
solution (in Hungarian), statistics
K. 134. A certain positive integer is divisible by 2, 5 and 9. Given that it has exactly 9 other positive factors, find the number.
(6 pont)
solution (in Hungarian), statistics
K. 135. Two decks of 32 German cards in each are shuffled separately, and one deck is placed on the top of the other. Then for each card in the upper deck its counterpart is found in the lower deck. The cards lying between the two cards are counted and the numbers obtained in this way are added. What will be the result?
(6 pont)
solution (in Hungarian), statistics
K. 136. A school took each of its students to a camp once during the summer. This was organized in two groups of the same number of students. 70% of the boys were in the first group and 80% of the girls were in the second group. What percentage of the students in the first group were boys?
(6 pont)
solution (in Hungarian), statistics
K. 137. The number of elements in set A is larger than the number of elements in set B, but less than the double of the number of elements in set B. Set B has 16 more subsets than set C. How many subsets may set A have?
(6 pont)
solution (in Hungarian), statistics
K. 138. 1 is subtracted from the square of an arbitrary prime number larger than 3. What is the largest positive integer that is always a factor of the result?
(6 pont)
 |
Problems with sign 'C'Deadline expired on November 15, 2007. |
C. 910. Nine integers that add up to 90 are written on the perimeter of a circle. Prove that there are four adjacent numbers that add up to at least 40.
(5 pont)
solution (in Hungarian), statistics
C. 911. Find the positive integers n for which n3+1 and n2-1 are both divisible by 101.
(5 pont)
solution (in Hungarian), statistics
C. 912. Is there a right-angled triangle in which the lengths a, b, c of the sides are integers, (a,b,c)=1 and the length of one median is 7.5?
(5 pont)
solution (in Hungarian), statistics
C. 913. The centre of the inscribed circle of triangle ABC is O, and the centre of the escribed circle drawn to side BC is K. On what condition will the quadrilateral BKCO be a kite? On what condition will it be a rectangle?
(5 pont)
solution (in Hungarian), statistics
C. 914. According to the trainer of a football team, the probability of a player to score a goal with a penalty kick is 95%. What is the probability that exactly three misses the goal out of five players?
(5 pont)
 |
Problems with sign 'B'Deadline expired on November 15, 2007. |
B. 4022. Is there a base of notation of numbers in which the rule for divisibility by 9 is the same as the rule for divisibility by 4 in decimal notation, the rule for divisibility by 4 is the same as the rule for divisibility by 9 in decimal notation, and divisibility by 7 can be decided by simply looking at the last digit?
(4 pont)
solution (in Hungarian), statistics
B. 4023. Construct two lines through a given point of one side of a triangle that divide the area of the triangle into three equal parts.
(3 pont)
solution (in Hungarian), statistics
B. 4024. How many numbers can be selected out of the first 1000 positive integers at most, so that the sum of no pair of selected numbers is divisible by their difference.
(3 pont)
solution (in Hungarian), statistics
B. 4025. A regular triangle is drawn on the side BC of a triangle ABC towards the outside, and one on the side CA towards the inside. The third vertices of the regular triangles are A* and B*, respectively. The reflection of vertex C in the line AB is C'. Prove that the points A*, B* és C' are collinear.
(4 pont)
solution (in Hungarian), statistics
B. 4026. The length of the common chord of two circles of diameters d1 and d2 is h. A line drawn through one of the intersections cuts the circles at the points C1 and C2, and the points D1 and D2, respectively, as shown in the Figure. Prove that the line C1D1 is only perpendicular to C2D2 if .
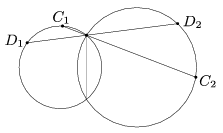
(4 pont)
solution (in Hungarian), statistics
B. 4027. Solve the following equation:
(4 pont)
solution (in Hungarian), statistics
B. 4028. The radii of two spheres are 5 and 3 units, and the distance of the centres is 4 units. Calculate the volume of their intersection.
(3 pont)
solution (in Hungarian), statistics
B. 4029. The sum of the positive numbers r and s is 1. Show that rr.ss+rs.sr 1.
1.
Suggested by R. F. Stöckli, Buenos Aires
(5 pont)
solution (in Hungarian), statistics
B. 4030. AB is a given line segment in the plane. Consider all arbitrary points C for which the triangle ABC is not isosceles. The exterior angle bisector of angle C intersects the line AB at D, and its intersection with the tangent drawn at point A to the circle ADC is P. Determine the locus of all possible points P.
From an Austrian competition problem
(5 pont)
solution (in Hungarian), statistics
B. 4031. Let n be an integer greater than 1. Prove that the equation
has no rational solution.
(5 pont)
 |
Problems with sign 'A'Deadline expired on November 15, 2007. |
A. 434. Points A, B, C lie inside the convex hexagon MNPQRS, such that the triangles ABC, NAM, PQB and CRS are similar. Let X, Y, Z be the midpoints of the line segments NP, QR, SM, respectively, and let G, K, I be the centroids of the triangles ABC, MPR and NQS, respectively. Prove that (a) If triangle ABC is equilateral then triangle GKI is equilateral; (b) Triangles ABC and XYZ are similar if and only if triangle ABC is equilateral.
Romanian competition problem
(5 pont)
A. 435. Prove
whenever 1 a,b,c
a,b,c 2.
2.
Vietnamese problem
(5 pont)
A. 436. Prove that
for every positive integer n.
(5 pont)
Upload your solutions above.
