A KöMaL 2008. januári matematika feladatai

Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.

Feladat típusok elrejtése/megmutatása:

K-jelű feladatok

A beküldési határidő 2008. február 11-én LEJÁRT.

K. 151. Egy diákcsoportban felmérést végeznek, és kiderül, hogy a fiúk $\frac{2}{3}$ része és a lányok $\frac{3}{4}$ része szereti a málnát. A felmérés eredményeképpen az is kiderült, hogy pont ugyanannyi fiú szereti a málnát, mint lány. A felmérésben szereplő diákok hányadrésze szereti a málnát?

(6 pont)

megoldás, statisztika

K. 152. Az Awr bolygó 800 lakosa 3%-ának 2 feje van, a többi lakos felének 3, felének csak egy. A szomszédos Bwr bolygóról épp most érkezik egy szállítmány gyümölcs: fejenként egy finom cwr mindenkinek. Pontosan mennyi?

(6 pont)

megoldás, statisztika

K. 153. Pisti egy négyjegyű számra gondol, és ezt Sanyinak kell kitalálnia. Ehhez Sanyi négyjegyű számokat mondhat, és Pisti minden tippnél megmondja, hogy hány olyan számjegy szerepel a tippben, amelyik a gondolt szám megfelelő helyiértéken álló számjegyével megegyezik. (Például, ha az 1234 a gondolt szám, és Sanyi tippje a 6231, akkor 2 számot talált el, a 2-t és a 3-at. Az 1 nem számít találatnak, mert nem azon a helyen áll a tippben, mint ahol a kitalálandó számban). Sanyi kilenc tippet mondott: 2186, 5127, 6924, 4351, 5916, 8253, 4521, 6384, 8517. Mind a kilenc tippben pontosan egy-egy számjegyet talált el, azaz mind a kilenc számban pontosan egy olyan számjegy van, amely a gondolt számban is ugyanazon a helyen áll, mint a tippben. Melyik számra gondolt Pisti?

(6 pont)

megoldás, statisztika

K. 154. Két szám különbsége, összege és szorzata úgy aránylik egymáshoz, mint 1:7:24. Melyik ez a két szám?

(6 pont)

megoldás, statisztika

K. 155. Az ábrán látható négyszögben

$DAB\sphericalangle = ABC\sphericalangle =60^\circ,$

valamint $CAB\sphericalangle =CBD\sphericalangle$ . Bizonyítsuk be, hogy AD+CB=AB.

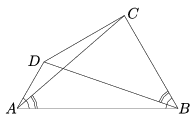
(6 pont)

megoldás, statisztika

K. 156. A körben lévő házikó alja négyzet, teteje szabályos háromszög. Bizonyítsuk be, hogy a ház oldalának hossza a kör sugarával egyezik meg.

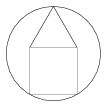
(6 pont)

megoldás, statisztika

C-jelű feladatok

A beküldési határidő 2008. február 15-én LEJÁRT.

C. 925. Mutassuk meg, hogy az

$\frac{x}{y^3-1}+\frac{y}{1-x^3}+\frac{2(x-y)}{x^2y^2+3}$

kifejezés helyettesítési értéke állandó minden olyan helyen, ahol a kifejezés értelmezve van és x+y=1.

(5 pont)

statisztika

C. 926. Egy tanteremben 24 lámpatestet szereltek fel, amelyek mindegyikébe 4-4 izzó fér el. Amikor néhány lámpába becsavarták a négy izzót, akkor már látszott, hogy a rendelkezésre álló készlet kevés lesz. A továbbiakban előbb hármasával, majd csak kettesével, végül egyesével tekerték be az izzókat a lámpatestekbe. Sajnos így is maradtak lámpák, amelyekbe nem jutott izzó. Hány izzó hiányzott, ha kétszer annyi lámpába került egy-egy izzó, mint ahányba négy, és fele annyi lámpába egyáltalán nem jutott, mint ahányba hármat is csavartak?

(5 pont)

megoldás, statisztika

C. 927. Adott egy derékszögű háromszög. Átfogóját c-vel jelölve területe $t=\frac{c^2}{8}$ . Adjuk meg a háromszög szögeinek pontos értékét.

(5 pont)

megoldás, statisztika

C. 928. Felírjuk az egész számokat 1-től egy 50-nel osztható n számig, majd elhagyjuk közülük az 50-nel oszthatókat. Mutassuk meg, hogy a megmaradt számok összege négyzetszám.

(5 pont)

megoldás, statisztika

C. 929. Egy négyzet alapú csonkagúla alapéle és minden oldaléle 4. Fedőlapjának éle 2. Legfeljebb mekkora távolságra lehet egymástól a csonkagúla két csúcspontja?

(5 pont)

megoldás, statisztika

B-jelű feladatok

A beküldési határidő 2008. február 15-én LEJÁRT.

B. 4052. Egy egyszerű gráfban ugróiskolának nevezünk egy olyan P₁,P₂,...,P_k utat, amelyben minden i-re a P_i csúcs fokszáma i. Legfeljebb hány csúcsa lehet egy ugróiskolának egy n csúcsú gráfban?

Javasolta: Mészáros Gábor

(4 pont)

megoldás, statisztika

B. 4053. Az $a_1, a_2, \ldots$ egész számokból álló sorozatnak végtelen sok pozitív és végtelen sok negatív eleme is van, továbbá minden n-re teljesül, hogy $a_1, a_2, \ldots, a_n$ páronként különböző maradékot adnak n-nel osztva. Hányszor szerepel a sorozatban a 2008?

(4 pont)

megoldás, statisztika

B. 4054. Egy háromszögbe írt kör sugara r. A körnek az oldalakkal párhuzamosan húzott érintői egy-egy kisebb háromszöget vágnak le az eredeti háromszögből. Bizonyítsuk be, hogy a kis háromszögekbe írt körök sugarának összege szintén r.

(3 pont)

megoldás, statisztika

B. 4055. Bizonyítsuk be, hogy minden n!-nál nem nagyobb pozitív egész szám felírható az n! legfeljebb n darab különböző osztójának összegeként.

(5 pont)

megoldás, statisztika

B. 4056. Egy hegyesszögű háromszög magasságpontja M, körülírt körének középpontja O, oldalai a<b<c. A c oldal egyenese, a b oldalhoz tartozó magasság és az MO egyenes az eredeti háromszöghöz hasonló, fordított körüljárású háromszöget határoz meg. Mekkorák a háromszög szögei?

Javasolta: Bodnár János (Budapest)

(4 pont)

megoldás, statisztika

B. 4057. Oldjuk meg az x⁶-6x+5=0 egyenletet.

(4 pont)

megoldás, statisztika

B. 4058. Egy háromszög szögei $\alpha$ , $\beta$ , $\gamma$ . Mennyi

sin $\alpha$ sin $\beta$ cos $\gamma$ +sin² $\gamma$

lehető legnagyobb értéke?

(4 pont)

megoldás, statisztika

B. 4059. Adott a síkon egy O pont. Mutassunk példát olyan, egymással nem egybevágó A és B háromszögekre, amelyekre igaz, hogy minden O középpontú körnek ugyanakkora területű része esik az A és B háromszögekbe.

2007. évi Schweitzer-feladat nyomán

(5 pont)

megoldás, statisztika

B. 4060. Határozzuk meg az összes olyan $f\colon \mathbb{R}\to\mathbb{R}$ függvényt, amelyre tetszőleges x, y valós számok esetén

f(x)+f(x+f(y))=2x+y.

(4 pont)

megoldás, statisztika

B. 4061. Adott az ABC és a PQR háromszög úgy, hogy az A pont felezi a QR, a P pont a BC oldalt. A QR egyenes felezi a BAC, a BC egyenes a QPR szöget. Bizonyítsuk be, hogy

AB+AC=PQ+PR.

(5 pont)

megoldás, statisztika

A-jelű feladatok

A beküldési határidő 2008. február 15-én LEJÁRT.

A. 443. Egy konvex hatszög kerülete p. Az oldalfelezőpontok által meghatározott hatszög kerülete p₁, és mindegyik szöge 120 fokos. Bizonyítsuk be, hogy

$p_1\le\frac{\sqrt3}2p.$

Vietnami versenyfeladat

(5 pont)

statisztika

A. 444. Az $f\colon \mathbb{R}\to\mathbb{R}$ függvény folytonos, és tetszőleges a>0 valós számra az $f(a),f(2a),f(3a),\ldots$ sorozat 0-hoz tart. Igazoljuk, hogy $\lim\limits_{x\to\infty}f(x)=0$ .

Cseh versenyfeladat

(5 pont)

statisztika

A. 445. Igazoljuk, hogy tetszőleges p prímszámhoz és r egész számhoz található olyan n nemnegatív egész, amire

$\binom{2n}{n}\equiv r\pmod{p}.$

(5 pont)

statisztika

A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:

megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.

(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

Már regisztráltál?
Új vendég vagy?