A KöMaL 2010. januári fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2010. február 10-én LEJÁRT. |
M. 302. Mérjük meg, mekkora a szánkó talpának tapadási és csúszási súrlódási együtthatója havon! (Ha nincs hó, akkor bármilyen talajon.)
Közli: Homoki-Nagy Olga, Monor
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2010. február 10-én LEJÁRT. |
P. 4214. Egy egyenletes mozgással haladó tehervonat 4 másodperc alatt halad el a szabad jelzést mutató jelzőlámpa mellett. Ezt követően 4 másodperc alatt halad el egy 40 méter hosszú, vele azonos sebességgel szemközt haladó szerelvény mellett. Milyen hosszú a vonat? Hány km/h a vonat sebessége?
Közli: Zsigri Ferenc, Budapest
(3 pont)
P. 4215. Függőlegesen felakasztott, nyújtatlan, lágy rugó alsó végére rögzítünk egy testet. Megmérjük, hogy a testet elengedve mennyi idő alatt ér le a pályája legmélyebb pontjára. Hányszorosa ez az idő egy ugyanekkora utat kezdősebesség nélkül, szabadeséssel befutó test mozgásidejének?
Közli: Szombathy Miklós, Eger
(4 pont)
P. 4216. Bizonyos mennyiségű héliumgáz az ábrán látható \(\displaystyle A\to B\) folyamatot végzi, \(\displaystyle p_{0}=10^5\) Pa, \(\displaystyle V_{0}=3~\rm dm^3\). Határozzuk meg a gáz nyomását és térfogatát abban a közbülső \(\displaystyle C\) állapotban, ameddig \(\displaystyle Q_{AC}=3700\) J hőt közlünk a gázzal!
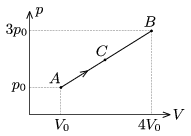
Közli: Kotek László, Pécs
(5 pont)
P. 4217. Ha a katódsugárcsőben az eltérítő lemezpár töltetlen, akkor az elektronágyúból kilépő elektronok változatlan sebességgel haladnak végig a csövön és csapódnak be az ernyőbe. Mit mondhatunk a becsapódási sebesség nagyságáról akkor, amikor a lemezpáron állandó nagyságú töltés van?
Közli: Szalay A. Sándor, Baltimore (USA)
(5 pont)
P. 4218. Mekkora áram folyik az ábrán látható \(\displaystyle A\) és \(\displaystyle X\), valamint az \(\displaystyle Y\) és \(\displaystyle B\) pontokat összekötő vezetékekben? Adatok: \(\displaystyle R=6~\Omega\), \(\displaystyle U=24\) V.
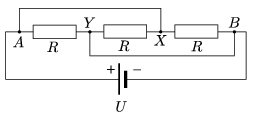
Közli: Holics László, Budapest
(4 pont)
P. 4219. Az ábrán látható ,,drótkeret'', amely szabadon el tud fordulni a függőleges \(\displaystyle PQ\) tengely körül, vízszintes irányú, homogén mágneses mezőben helyezkedik el. \(\displaystyle B=0{,}05\) T, \(\displaystyle r=0{,}05\) m, \(\displaystyle \ell=0{,}3\) m. A drótban \(\displaystyle I=10\) A áram folyik, tömege méterenként 10 dkg.

Mekkora rezgésidővel végezhet kis amplitúdójú rezgéseket ez a ,,drótkeret''?
Közli: Kungl Ákos, Veszprém, Lovassy L. Gimn.
(5 pont)
P. 4220. Egy merülőforraló teljesítménye 230 V-os szinuszos hálózat esetén 350 W.
\(\displaystyle a)\) Mekkora a merülőforraló legnagyobb és legkisebb pillanatnyi teljesítménye működés közben?
\(\displaystyle b)\) Mekkora a merülőforralón áthaladó áram legnagyobb pillanatnyi értéke?
\(\displaystyle c)\) Miért nem szabad a merülőforralót még a vízbe helyezés előtt bekapcsolni?
Közli: Vannay László, Budapest
(3 pont)
P. 4221. Egy egyenlőszárú prizma törőszöge \(\displaystyle 40^\circ\), üvegének törésmutatója 1,5. Mekkora beesési szöggel kell a fénysugárnak az egyik törőfelületre érkeznie, hogy a prizmában a fénysugár a prizma alapjával párhuzamosan haladjon? Hogyan módosul a válasz, ha a prizma 1,33 törésmutatójú vízbe, vagy 1,6 törésmutatójú benzolba merül?
Közli: Kobzos Ferenc, Dunaújváros
(4 pont)
P. 4222. Háromszorosan ionizált UF\(\displaystyle {}_{6}\) molekulákat gyorsítunk 5 kV feszültséggel, majd egy piciny nyíláson 1 T indukciójú mágneses mezőbe vezetjük őket. Az indukcióvektor merőleges a sebességre.
\(\displaystyle a)\) Milyen pályán mozognak az ionok? Adjuk meg a 238-as, illetve a 235-ös uránizotópot tartalmazó ionpályák jellemző paramétereit!
\(\displaystyle b)\) Ezen a módon szét lehet választani a 235-ös és a 238-as izotópokat egymástól. A második világháború alatt az USA-ban rendelkezésre álló ionforrások 1 mA-es ionáramot tudtak előállítani. Mennyi ideig tartott volna 1 kg teljesen tiszta 235-ös urán előállítása ezzel a módszerrel?
Szilárd Leó nukleáris verseny, Paks
(4 pont)
P. 4223. Elhanyagolható sebességű \(\displaystyle {}^7_{3}\)Li atommaggal nagy energiájú proton ütközik. A keletkező két \(\displaystyle \alpha\)-részecske derékszögben repül szét. Legalább mekkora volt a proton sebessége?
Varga István (1952-2007) feladata
(5 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

