KöMaL Problems in Informatics, April 2010
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'I'Deadline expired on May 10, 2010. |
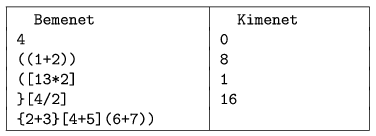
I. 238. Parentheses are used to change the priority of operations. Your program i238 should find unmatched parentheses or missing characters in an expression. Expressions can consist of three different types of parentheses, digits and arithmetic operations. (Checking other aspects of syntactic correctness is not to be considered now.)
Parenthetically correct expressions (,,szabályosan zárójelezett kifejezések'' in the example) are defined recursively:
- if string s is parenthetically correct (\(\displaystyle s\) may be empty as well), then so are (s), [s] and {s};
- if strings s and p are parenthetically correct expressions, then so is their concatenation sp.
Any other types of expression should be considered as incorrect (,,szabálytalanok'' in the example).

The first command line argument of your program is the name of a file containing several test expressions. The first line of the file contains an integer \(\displaystyle N\) (\(\displaystyle 1\le N\le 100\)), the number of test expressions, while the following \(\displaystyle N\) lines contain the expressions, each with length between 1 and 255.
The second command line argument of your program is the name of the output file, containing N lines, each having a single integer, specifying the position of the first incorrect or missing character in the corresponding line.
In the example, ,,Bemenet'' is input, while ,,Kimenet'' is output.
The source code (i238.pas, i238.cpp, ...) together with a short documentation (i238.txt, i238.pdf, ...) -- also describing which developer environment to use for compiling, further a brief description of your solution -- should be submitted in a compressed file (i238.zip).
(10 pont)
solution (in Hungarian), statistics
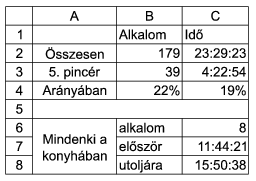
I. 239. Five busy waiters are working in a popular restaurant. The manager however suspects that they are spending too much time in the kitchen unnecessarily. To investigate this, the manager puts small radio transmitters on the waiters, so the time instant of each waiter entering into or exiting from the kitchen is recorded. (In the example, ``Be'' is ``into the kitchen'', while ``Ki'' is ``out of''.) We know that initially each waiter stayed outside the kitchen. You should analyse the data obtained, according to the description and examples below by using a spreadsheet application.
[1.] Data from file hazai.txt should be copied into cells beginning with A10, then the sheet should be saved as ,,pincer'' in the default format of your application.
[2.] Text cells A1:C8 should be formatted as in the example, while cells containing numeric data should be filled in with results of the tasks below.
[3.] Cell B2 should contain the total number of entries into the kitchen. (In the example, ,,Összesen'' is ,,Totals'', ,,Alkalom'' is ,,Number of occasions'', ,,Idő'' is ,,Duration'' or ``Time instant'', ``Mindenki a konyhában'' is ``Everybody in the kithcen'', while ``először'' and ``utoljára'' are ``for the first time'' and ``for the last time''.)
[4.] Cell C2 should contain the total time waiters spent in the kitchen.
[5.] Cell A3 should contain the identification number of the transmitter. (In the example, ,,pincér'' is ,,waiter''.)
[6.] Cell B3 should contain the number of entries into the kitchen of waiter specified by cell A3.
[7.] Cell C3 should contain the total time the waiter specified by cell A3 spent in the kitchen. Auxiliary cells to the right of column E can be used for computations.
[8.] The 4th row should contain the ratio between the corresponding data of the waiter specified by cell A3 and the totals. (In the example, ,,Arányában'' is ,,Proportionally''.)
[9.] In column D, beginning with the 11th row, you should specify the number of waiters simultaneously in the kitchen after the entry or exit in the actual row has taken place.
[10.] Cell C6 should contain the number of time intervals with each waiter staying in the kitchen.
[11.] Find the first time instant of the first and last intervals when all waiters were simultaneously in the kitchen. Auxiliary computations can be placed to the right of column E.
[12.] Measurements could have been performed easier by recording only the fact of crossing through the kitchen door, without knowing the direction. In this setting, the direction in column C should have been determined by you. By using data from column B, prove the above statement by determining the missing directional information and placing it into column E. You should apply formulae which can be copied flawlessly in the whole column.
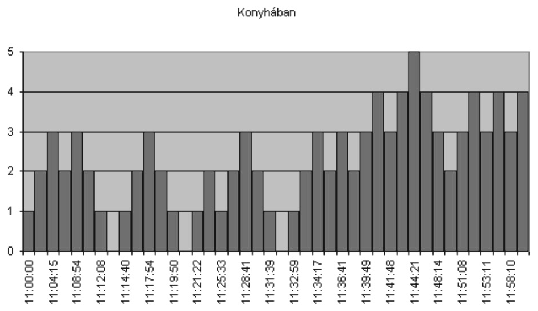
[13.] Create a diagram similar to the example showing the number of waiters in the kitchen versus time, until noon. (In the example, ,,Konyhában'' means ,,In the kitchen''.)
Your spreadsheet (i239.xls, i239.ods, ...) together with a short documentation (i239.txt, i239.pdf, ...) -- also describing the name and version number of the spreadsheet application, further a brief description of your solution -- should be submitted in a compressed file (i239.zip).
(10 pont)
I. 240. In a certain laboratory a chain of supercells is being developed, so they measure its operating temperature. Devices record and store temperature data of elements of the chain in tabulator-separated text files of size (n+1).(m+1). Here number n denotes the length of the chain, while m is the number of measurements. The first piece of data of the file is the identifier of the chain, further data in the first row contain the identifier of cells in the chain, while further data in the first column refer to the measurement times.
Our task is to process the data copied from the text file into an empty spreadsheet (such that the first piece of data is copied into cell A1) with possibly one keystroke combination, according to the description below.
The first row and column should be formatted by using yellow background and bold blue characters and temperature data should contain oC as a unit. Values above the critical temperature 70 oC should be denoted by bold red characters. You should create a line chart with the horizontal axis containing the identifiers of the supercells in the chain. The legend of the diagram should contain the time instants, while the label of the diagram should be the identifier of the whole chain.
The difficulty of the problem lies in the fact that values of n and m are unknown, what is known that they are at most 10. To solve the problem, you should create a macro in Microsoft Excel (2003 or 2007) or in OpenOffice.org 3.x.
Your spreadsheet containing the macro (i240.xls, i240.ods, ...) together with a documentation (i240.txt, i240.pdf, ...) -- also describing the name and version number of the spreadsheet application, further a brief description of your solution--should be submitted in a compressed file (i240.zip). Finally, the macro itself should also be submitted in a separate text file i240m.txt.
(10 pont)
 |
Problems with sign 'S'Deadline expired on May 10, 2010. |
S. 53. In this exercise we are going to do some treasure hunting again. Strategies now are different, because spy satellites can also be used. However, collecting the treasure fast still remains a challenge.
Write your program to collect treasure with the highest possible total value provided that location and value of the pieces, further a time limit for hunting are specified. Your program should decide which pieces of treasure should be picked up and in what order. You can neglect the time needed to pick up a single piece when you have touched it. You can start hunting from any piece. You cover one unit of distance in each time unit.
The map is read from the standard input. The first line contains two integers separated by a space: the number of pieces 1 N
N 1000 and the time limit
1000 and the time limit .
The following N lines then contain 3 integers each (separated by a space): coordinates of the ith piece 0 Xi,Yi
Xi,Yi 10000 and its value 0
10000 and its value 0 Ci
Ci 1000.
1000.
Your solution should be written to the standard output. The first line should contain the number of pieces 1 K
K N your program can collect, while the following K lines contain the number of the pieces to be collected in order (indexing begins with 1).
N your program can collect, while the following K lines contain the number of the pieces to be collected in order (indexing begins with 1).
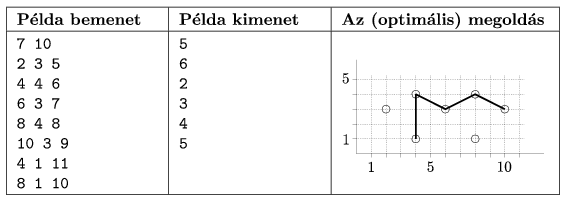
In the example, ,,Példa bemenet'' is sample input, ,,Példa kimenet'' is sample output, while ,,Az (optimális) megoldás'' is the (optimal) solution.
Your solution does not have to be optimal. Submitted solutions are ranked according to their running times in different test cases. The best program gets 10 points, the next one 9 points, while other programs 8 points.
Programs are run on a 2 GHz processor with Core 2 architecture. Your program is allowed to spend at most 10 minutes on each test case, otherwise the actual test case will not be taken into account.
The source code (s53.pas, s53.cpp, ...) together with a short documentation (s53.txt, s53.pdf, ...) -- also describing which developer environment to use for compiling, further a brief description of your solution -- should be submitted in a compressed file (s53.zip).
(10 pont)
$Var(Body)
Upload your solutions above
