KöMaL Problems in Mathematics, November 2010
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on December 10, 2010. |
K. 265. A man commutes to work by train. Every day in the afternoon, he arrives to the railway station with the same train, and his wife drives him home. The wife leaves home just in time to arrive at the station when her husband's train comes in. One day, the man arrived at the station an hour earlier, and started to walk home along the road on which his wife drove him home every day. The wife left home at the usual time. When she saw her husband on the road, she immediately stopped, picked him up and turned around. They arrived home 20 minutes earlier than usual. Calculate the time in minutes that the husband walked along the road.
(6 pont)
solution (in Hungarian), statistics
K. 266. Let a, b, c, d denote positive integers. Given that , show that
always lies between
and
.
(6 pont)
solution (in Hungarian), statistics
K. 267. Given that , where
and
are two-digit numbers and
is a three-digit number, determine the values of the digits in the addition if c=0.
(6 pont)
solution (in Hungarian), statistics
K. 268. How long is the radius of the circle in which a chord of length 6 units is twice as far away from the centre as a chord of length 12 units?
(6 pont)
solution (in Hungarian), statistics
K. 269. Explain why there is no pair (x,y) of integers such that xy(x2-y2)=2925?
(6 pont)
solution (in Hungarian), statistics
K. 270. A fair bookmaker only takes fair bets. For example, if you bet 3 to 5 on something, it means that you pay 3 if you lose and get 5 if you win, but in the long run no one gains anything on this bet. There are three horses running a race: Curse, Worse, and Hearse. The fair bookmaker takes 2 to 1 bets on Hearse winning the race, and 3 to 7 bets on Curse winning. (These are fair bets.) In what ratio can one bet on Worse coming in first?
(6 pont)
 |
Problems with sign 'C'Deadline expired on December 10, 2010. |
C. 1050. Currently there are six different kinds of banknotes in Hungary: 500, 1000, 2000, 5000, 10000 and 20000 forint notes. How many different sums of money can be paid with three notes?
(5 pont)
solution (in Hungarian), statistics
C. 1051. A natural number n is chosen between two consecutive square numbers. The smaller square is obtained by subtracting k from n, and the larger one is obtained by adding l to n. Prove that the number n-kl is a perfect square.
(5 pont)
solution (in Hungarian), statistics
C. 1052. T is the foot of the perpendicular drawn from vertex A of an acute-angled triangle ABC to side BC. The feet of the perpendiculars drawn from T to the sides AB and AC are P and Q. Prove that the quadrilateral BPQC is cyclic.
(5 pont)
solution (in Hungarian), statistics
C. 1053. Prove that the sum (2n-1)2n+1+(2n+1)2n-1 is divisible by 4.
(Based on the idea of G. Holló, Budapest)
(5 pont)
solution (in Hungarian), statistics
C. 1054. F is the midpoint of edge BC of the unit cube ABCDA1B1C1D1, O is the centre of the square DCC1D1. The plane of triangle AFO cuts the cube into two solids. Find the ratio of the volumes of the two parts.
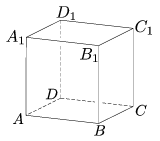
(5 pont)
 |
Problems with sign 'B'Deadline expired on December 10, 2010. |
B. 4302. Soldiers are lined up along a line in the east-west direction, each of them facing north. The officer commands ``right turn''. Then they should all turn towards the east but, since they are at the very beginning of their military career, some of them get the order wrong and turn towards the west. Every soldier who now faces his neighbour concludes that they have made a mistake (disregarding the possibility of the neighbour making the mistake), and they make a 180-degree turn within 1 second. Then the process continues in the same way: every soldier who faces a neighbour makes a 180-degree turn within 1 second. Prove that the process will end in a finite number of steps.
(Talent Search, U.S.A.)
(3 pont)
solution (in Hungarian), statistics
B. 4303. A rectangle that is not a square is folded in two along a diagonal. Prove that the perimeter of the resulting pentagon is smaller than the perimeter of the original rectangle.
(3 pont)
solution (in Hungarian), statistics
B. 4304. Is there a positive integer k, such that ?
(3 pont)
solution (in Hungarian), statistics
B. 4305. What is the largest possible number of edges of a pyramid with an n-sided base that a plane may intersect?
(4 pont)
solution (in Hungarian), statistics
B. 4306. Solve the equation 16x2+y+16y2+x=1.
(Competition problem from Transsylvania)
(4 pont)
solution (in Hungarian), statistics
B. 4307. Given two points on each of two sides of triangle ABC, prove that at least one of the four triangles formed by the four points has an area that is not greater than one quarter of the area of triangle ABC.
(L. Surányi, Budapest)
(4 pont)
solution (in Hungarian), statistics
B. 4308. Given the quadrilateral ABCD, show that the Feuerbach circles of triangles ABC, ABD, ACD and BCD have a point in common.
(Sz. Miklós, Herceghalom)
(5 pont)
solution (in Hungarian), statistics
B. 4309. Find the smallest possible positive integer n for which 32n-1 is divisible by 22010?
(4 pont)
solution (in Hungarian), statistics
B. 4310. Let be positive numbers, such that ak+1-ak
 1 for all k=0,1,...,n-1. Show that
1 for all k=0,1,...,n-1. Show that
(IMC 2010 -- Blagoevgrad, Bulgaria)
(5 pont)
solution (in Hungarian), statistics
B. 4311. P is a given point in the interior of the acute-angled triangle ABC. The lines AP, BP and CP intersect the opposite sides at the points A1, B1 and C1, respectively. Given that PA1=PB1=PC1=3 and AP+BP+CP=43, prove that AP.BP.CP=441.
(A. Máder and V. Vigh, Szeged)
(4 pont)
 |
Problems with sign 'A'Deadline expired on December 10, 2010. |
A. 518. How many distinct subsets A1,...,At of an n-element set can be chosen such that for all 1
 i<j<k
i<j<k t?
t?
(Miklós Schweitzer Competition, 2010)
(5 pont)
A. 519. Let n 3 and k be positive integers. We place n coins on the table with the heads sides up. Then the following operation is performed k times: we choose one of the n coins randomly, with equal probabilities, and flip that coin. Prove that the probability that the procedure results in all the n coins lying with tails up is less than
3 and k be positive integers. We place n coins on the table with the heads sides up. Then the following operation is performed k times: we choose one of the n coins randomly, with equal probabilities, and flip that coin. Prove that the probability that the procedure results in all the n coins lying with tails up is less than .
(Suggested by L. Rónyai and G. Kós)
(5 pont)
solution (in Hungarian), statistics
A. 520. Is there any infinite sequence a1,a2,... of nonnegative numbers for which is finite and
(Miklós Schweitzer Competition, 2010)
(5 pont)
Upload your solutions above.
