A KöMaL 2010. decemberi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2011. január 10-én LEJÁRT. |
I. 253. Az alábbi feladatban egy olyan faluvégi utcát vizsgálunk, amelynek csak az egyik oldalán laknak. A helyi szokásoknak megfelelően minden portát festett fakerítés határol, a ház pedig a kerítéstől kicsit bentebb található. Egy-egy porta kerítése egyszínű.
Az utca portáit leíró adatokat az utca.txt állomány tartalmazza. Az állomány sorai az utca portáit valós elhelyezkedésük sorrendjében (az alsó végtől a felső végig) adják meg. A sorok két számot és egy, legfeljebb 20 karakteres szót tartalmaznak. Az első szám a porta utcafront oldali hosszát adja meg méterben (másik kiterjedésükben egyeznek), a másik pedig a kapunak a porta sarkától mért távolságát. (A most pontszerűnek tekintett kapu soha nem kerül telekhatárra.) A szó a kerítés színét adja meg. Az utca hossza legfeljebb 10 km.
Például:
15 3 sarga
18 5 kek
11 4 sarga
...
A 2. sor szerint az utca alsó végtől számított második portájának utcahossza 18 méter, a sarkától 5 méterre, az utca elejétől 20 méterre van.
Készítsünk programot, amely az alábbi kérdésekre válaszol. A program forráskódját porta néven mentsük.
A képernyőre írást igénylő részfeladatok eredményének megjelenítése előtt írjuk a képernyőre a feladat sorszámát. Amennyiben a felhasználótól kérünk be adatot, jelenítsük meg a képernyőn, hogy milyen értéket várunk (például 4. feladat: Kérem a lámpaoszlopok távolságát!).
1. Olvassuk be az utca.txt állományban talált adatokat, s annak felhasználásával oldjuk meg a következő feladatokat.
2. Adjuk meg, hány olyan telek van az utcában, amelynek kerítése piros színű.
3. Határozzuk meg, hogy a legnagyobb telek területe hányszorosa a legkisebbnek. Az eredményt két tizedes pontossággal jelenítsük meg.
A faluban most készül a közvilágítás. Az utca kezdetére, a sarokra kerül egy villanyoszlop, majd v méterenként egy-egy újabb. Minden lámpa a kerítésnek ugyanolyan hosszú szakaszát képes megvilágítani, az előtte lévő l métert és az utána levő l métert. v és l egész számok, valamint v 2l, azaz a fénykörök legfeljebb érintik egymást.
2l, azaz a fénykörök legfeljebb érintik egymást.
4. Kérjük be a felhasználótól v és l értékét. A további feladatok megoldásánál ezeket az értékeket használjuk.
5. Állítsuk elő az utca villanyoszlopokkal kiegészített képét a kep.txt állományban. Az első sorban a kerítések jelenjenek meg, a másodikban a villanyoszlopok. A telekhatárokat a szűrő karakter (|) jelezze, a kaput szóköz. A kerítést színének első karaktere jelölje. A villanyoszlopokat az O betű adja meg. A feladat elején szereplő példának az alábbi képrészlet felel meg 6 méteres oszloptávolság esetén (csak a két szürke hátterű sort kell a kimenetnek tartalmaznia):
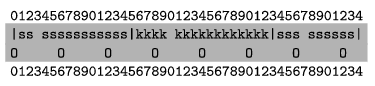
6. A világítás sokba kerül, ezért az utca lakói elhatározzák, hogy amíg senki nincs az utcán, csak annyi lámpát tartanak égve, amennyi elegendő az összes kapu megvilágításához. A bekapcsolt lámpák sorszámának meghatározásához a következő algoritmust is használhatjuk.
Ciklus amíg van meg nem világított kapu
Keresd meg az első ilyen kaput!
Határozd meg, melyik az utolsó lámpa, ami megvilágítja!
Ciklus vége
A bekapcsolt lámpák sorszámát egymástól szóközzel elválasztva jelenítsük meg a képernyőn.
7. A lakók ráébredtek, hogy ez még mindig túl sokba kerül, ezért arra jutottak, hogy egy lámpa csak addig világítson, amíg valaki ebben az utcában tartózkodik, és a fénykörében van. Határozzuk meg, hogy mennyi az egyes lámpák világítási idejének összege, ha valaki 100 méter/perc sebességgel sétál végig az utcán közvetlenül a kerítés mentén. A világítási időt percben jelenítsük meg a képernyőn.
Beküldendő egy tömörített i253.zip állományban a program forráskódja (i253.pas, i253.cpp, ...), valamint a program rövid dokumentációja (i253.txt, i253.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
(10 pont)
I. 254. Egyre több dokumentum mögött van ott -- általában közvetlenül nem látható módon -- az XML. Ezen dokumentumok lehetnek szövegesek, táblázatok, de akár adatbázisok is. Az adatbázisok esetén megszokhattuk, hogy az adatokat egy jól meghatározott szerkezetben tároljuk el. Ez a szerkezet XML használata esetén is megalkotható, XML sémának nevezik. Az XML séma egy speciális XML dokumentum, XSD kiterjesztéssel jelölik.
Készítsük el a diákkal kapcsolatosan tárolt személyes adatok rögzítésével kapcsolatos XML-sémát. A diákok és szülők személyes adataira gondoljunk, tehát a tanulmányi, fegyelmi, hiányzási adatokra nincs szükség. A séma elkészítésénél ügyeljünk arra, hogy az a valósághoz, mindennapi élethez minél inkább igazodjon, azaz lehetséges, hogy valakinek több e-mail címe vagy telefonszáma van, esetleg valamely szülő nem ismert.
A kötelező adatokat a Közoktatási törvény 2. számú mellékletében a ,,A gyermekek, tanulók adatai'' rész 1a és 1b pontjában találjuk meg. Egészítsük ki ezt a diák osztályával és az osztályfőnök nevével, valamint néhány olyan adattal, amellyel a séma itt nem használt lehetőségeit is kihasználja/bemutatja.
Munkánkat a http://www.xmlme.com/Validator.aspx lapon online módon is ellenőrizni tudjuk.
Beküldendő az i254.xsd XML séma, a sémának megfelelő, néhány adatot tartalmazó i254.xml dokumentum egy i254.zip fájlba tömörítve.
(10 pont)
I. 255. Ismert játék, illetve fizikai demonstrációs eszköz az ingasor (Newton bölcsője). A kísérlet az energia- és a lendület-megmaradás törvényét mutatja be.

Készítsük el gif-animációs szerkesztőprogrammal a kísérlet szimulációját. A megoldáshoz ajánljuk a Stykz vagy a Pivot Stickfigure Animator nevű (internetről ingyenesen letölthető) programot. (A programokról rövid leírás olvasható a http://blog.sulinet.hu/oktinf/ oldalon, illetve oktatófilmek találhatók az ismert videó-megosztókon.)
A szimulációhoz három animációt készítsünk, amelyek 1, 2 illetve 3 golyó kitérítése után a tökéletesen rugalmas ütközés utáni mozgást mutatják be. Az animációkhoz végtelenített lejátszást és megfelelő képváltási sebességet állítsunk be.
Beküldendő tömörített állományban (i255.zip) az animációk gif, valamint forrásállománya a szerkesztőprogram alapértelmezett formátumában és egy rövid dokumentáció (i255.txt, i255.pdf, ...), amely tartalmazza vázlatosan a megoldás leírását és a használt szoftver nevét.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2011. január 10-én LEJÁRT. |
S. 58. A Bergengóc Királyságban évezredes hagyományokkal rendelkező esemény a Nemzetközi Máguskonferencia, melynek minden évben az egyik legkedveltebb és leglátványosabb műsorszáma a Nagyotmondók Viadala. Ennek keretében az ország legkiválóbb mágusai mérik össze tudásukat: a nyertes az, aki a rendelkezésre álló időkeret alatt a leghosszabb varázsszót mondja ki -- a legkülönfélébb csodás mellékhatásokkal.
Sajnos az előző évben a rendezvény túlontúl látványosra sikeredett, s a konferencia után a főváros helyreállítása hónapokig tartott. Ennek megelőzése érdekében a király idén elrendelte, hogy a versenyen kizárólag olyan varázsszavakkal lehet indulni, melyek előállnak páros hosszú tükörszavak egymás után írásával, ezekről ugyanis köztudott, hogy veszélytelenek.
Készítsünk programot, mely a versenyzők által előadni kívánt, előzetesen leadott varázsszavakról eldönti, hogy a fenti módon felbonthatók, azaz a versenyen biztonsággal előadhatóak-e, és ha igen, akkor meg is ad egy-egy ilyen felbontást.
A standard bemenet első sorában egyetlen egész szám: a vizsgálandó varázsszavak N száma szerepel (1 N
N 100), azt ezt követő N darab sor pedig egy-egy varázsszót tartalmaz. Feltehetjük, hogy minden varázsszó kizárólag az angol ábécé kisbetűiből áll, legfeljebb 1 000 000 karakter hosszú, illetve -- amennyiben biztonságos -- legfeljebb 5000 karakter hosszú tükörszavakból épül fel.
100), azt ezt követő N darab sor pedig egy-egy varázsszót tartalmaz. Feltehetjük, hogy minden varázsszó kizárólag az angol ábécé kisbetűiből áll, legfeljebb 1 000 000 karakter hosszú, illetve -- amennyiben biztonságos -- legfeljebb 5000 karakter hosszú tükörszavakból épül fel.
A standard kimenetre pontosan N darab sor kerüljön, az i-edik sor a bemenet i-edik varázsszavának értékelését tartalmazza. Amennyiben a varázsszó biztonságos, akkor a sor elején a felbontásban szereplő részszavak K száma szerepeljen (K 1), majd ezt kövessék a felbontás elemei, szóközzel elválasztva. Ellenkező esetben a sorba mindössze egy ,,0'' számjegyet írjunk. Több megoldás esetén bármelyik megadható.
1), majd ezt kövessék a felbontás elemei, szóközzel elválasztva. Ellenkező esetben a sorba mindössze egy ,,0'' számjegyet írjunk. Több megoldás esetén bármelyik megadható.

Beküldendő a feladat megoldását tartalmazó forrás és projektállományok (az .exe és más a fordító által generált kiegészítő állományok nélkül), valamint a megoldás menetét röviden bemutató dokumentáció (s58.txt, s58.pdf, ...) egy tömörített mappában (s58.zip).
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

