KöMaL Problems in Physics, May 2011
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on June 10, 2011. |
M. 315. Measure how long it takes for a single pulse initiated at one end of a slinky, which is stretched along a horizontal tabletop, to travel back. Examine how the speed of the pulse depends on the previously fixed length of the slinky. Initiate both transverse and longitudinal short pulses.
(6 pont)
 |
Problems with sign 'P'Deadline expired on June 10, 2011. |
P. 4348. A tree on the opposite shore of a smooth surface of water of width of several tens of meters covers a house, which is behind the tree, such that only the top of the chimney of the house can be seen. Observing the image of the tree reflected from the surface of water the image of top of the chimney cannot even be seen. How can it happen?
(3 pont)
solution (in Hungarian), statistics
P. 4349. The gauge pressure of the tire of a car is 250 kPa at a temperature of 10 oC. How and by what amount does this gauge pressure change if the temperature increases to 25 oC? The ambient air pressure is 100 kPa the volume of the air in the tire cannot increase at this pressure.
(3 pont)
solution (in Hungarian), statistics
P. 4350. A ball collides with another, stationary ball. The collision is head on and elastic. The change in the velocity of the moving ball is 20 m/s. The ratio of the masses of the moving and the stationary ball is 3:5. What was the initial speed of the moving ball?
(4 pont)
solution (in Hungarian), statistics
P. 4351. A rod of length L=35 cm, and of negligible mass is held at an unstable equilibrium on a horizontal frictionless plane. Small balls of mass m=0.2 kg are attached to the ends of the rod. At a certain instant the rod is released. a) What are values of the kinetic energy of the balls when the ball initially at the top hits the ground? b) What are the velocities (both magnitude and direction) of the balls when the angle between the rod and the vertical is 60o?
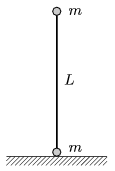
(5 pont)
solution (in Hungarian), statistics
P. 4352. A rough inclined plane of height h=2 m, and of angle of elevation 20o consists of two parts. The two parts have the same length but the friction is different on them. At the bottom of the slope a small body was pushed, and it slid to the top of the plane and then it slid back and it just stopped at the end of the slope. a) What was the initial speed of the small body at the bottom of the slope? b) What is the coefficient of friction along the bottom part of the slope if the coefficient of friction at the top is 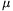 2=0.3?
2=0.3?
(4 pont)
solution (in Hungarian), statistics
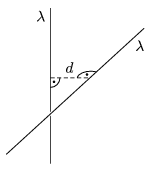
P. 4353. Two very long plastic rods are placed perpendicularly at a distance of d. They are both charged uniformly, their linear charge density is 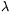 . Calculate the repelling force between them.
. Calculate the repelling force between them.
(6 pont)
solution (in Hungarian), statistics
P. 4354. A 12 cm long bar magnet is placed vertically above the centre of a horizontal, fixed, open conducting ring, such that the lower end of the magnet is 4 cm from the centre of the ring. The magnet is dropped and when its lower end reaches the plane of the ring the induced e.m.f. between the ends of the ring is +2 V. What are the magnitude and the polarity of the induced e.m.f. at the instants when the centre of the magnet, and when the upper end of the magnet passes the centre of the ring?
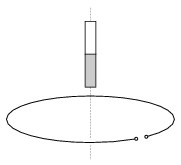
(4 pont)
solution (in Hungarian), statistics
P. 4355. ccording to www.mavir.hu on 1. December 2010 the average daily electrical power demand of Hungary was 5151 MW, but between 7 and 22 hours it was 496 MW greater than this, and in the rest of the day it was 827 MW smaller. If all the electrical energy was generated in nuclear power stations (the power generated by nuclear power plants is constant) then the variation of the power demand could be compensated by pumped-storage hydroelectric power plants. Estimate the size of the water reservoirs that are needed if they are placed to a height of
a) 20 m,
b) 500 m.
(4 pont)
solution (in Hungarian), statistics
P. 4356. a) Two diffraction gratings are placed onto each other such that their slits are perpendicular to each other. Can light pass through them?
b) Two perpendicular polarisers are placed onto each. Can light pass through them?
c) What happens if a third polariser is placed between the two mentioned in question b)?
(4 pont)
solution (in Hungarian), statistics
P. 4357. An electron enters to a region of uniform electric field, which is perpendicular to its velocity. The speed of the electron is 60% of the speed of light. When it leaves the region where there is electric field the angle between its original and final velocity is 45o. a) What is the speed of the electron when it leaves the region of the electric field? b) What is the displacement d of the electron, if the electric field strength is E=510 kV/m? (The rest energy of the electron is m0c2=510 keV.)
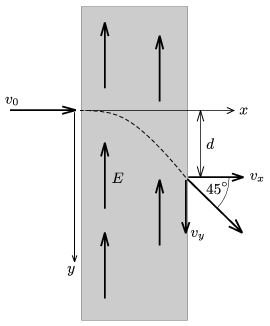
(5 pont)
solution (in Hungarian), statistics
P. 4358. In the Universe there are more Neon than Argon atoms. On the contrary in the atmosphere of the Earth there are 500 times as much Argon as Neon atoms. How can it happen?
(4 pont)
Upload your solutions above.
