A KöMaL 2011. novemberi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2011. december 12-én LEJÁRT. |
K. 307. Az ábrán látható téglalapot négyzetekre osztottuk fel hézagmentesen. Az A négyzet területe 196 cm2, a B négyzet területe 16 cm2, a C négyzet területe 81 cm2. Mennyi az eredeti téglalap területe?
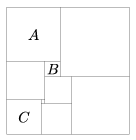
(6 pont)
K. 308. Egy müzlit háromféle kiszerelésben árulnak, ezek piros, zöld és kék színű dobozban kerülnek forgalomba. A piros doboz 50%-kal drágább, mint a kék, és 20%-kal kevesebb a tömege, mint a zöldnek. A zöld dobozosnak 50%-kal nagyobb a tömege, mint a kéknek, és 25%-kal drágább, mint a piros. Melyiknek a legkisebb a kilogrammonkénti ára?
(6 pont)
K. 309. A síkot két egyenes négy szögtartományra osztja. Nem feltétlenül ebben a sorrendben, fokokban mérve ezek nagysága: 5x-9, 4x+27, x+y-30, y-x+3z. Mekkorák lehetnek a szögek?
(6 pont)
K. 310. Két 90 és 100 közötti szám szorzására kitaláltunk egy szabályt: adjuk össze a két számot, majd vonjunk ki az összegből 100-at, végül írjuk az előző eredmény után az eredeti számok 100-tól való eltérésének szorzatát. Pl.: a 97 és a 94 esetén: 97+94-100=91 és (100-97)(100-94)=18, tehát a szorzat 9118, és valóban, 97×94=9118.
Miért jó ez az eljárás? Hogyan lehetne bármely két kétjegyű szám közötti szorzásra kiterjeszteni?
(6 pont)
K. 311. A 772009+772010+772011+772012 láthatóan osztható 7-tel és 11-gyel. Adjuk meg az összes prímszámot, amivel osztható ez a szám.
(6 pont)
K. 312. A koordináta-rendszer első síknegyedében elhelyezkedő ABCD trapéz csúcsai: A(a;0); B(8;b); C(3;b); D(0;0), ahol a és b egész számok. Tudjuk, hogy a trapéz területe 121. Adjuk meg a hiányzó koordinátákat!
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2011. december 12-én LEJÁRT. |
C. 1095. Melyik szorzat a nagyobb:
vagy
?
(5 pont)
C. 1096. Egy kocka élének hossza egész szám. Vegyük az élhossz harmadát, az egyik oldallap területének felét és a térfogat hatodát. Igazoljuk, hogy a három szám összege egész.
(5 pont)
C. 1097. Új gumiabroncsot szerelünk egy motorkerékpár mindkét kerekére. Egy abroncs akkor tekinthető teljesen elkopottnak, ha a hátsó keréken 15 000 km-t, vagy az első keréken 25 000 km-t futott. Legfeljebb hány kilométert futhat a motor a gumik teljes elkopásáig, ha megfelelő időben az első gumit felcseréljük a hátsó gumival?
(5 pont)
C. 1098. Bizonyítsuk be, hogy ha egy konvex érintőnégyszög két szemközti szöge derékszög, akkor ez a négyszög deltoid.
(5 pont)
C. 1099. Az ABCD négyszögben M az AB, N pedig a CD szakasz felezőpontja. Az AC és BD átlók hossza , és 60o-os szöget zárnak be. Mekkora az MN szakasz?
Javasolta: Dávid Géza (Matlap, Kolozsvár)
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2011. december 12-én LEJÁRT. |
B. 4392. A 20×20-as sakktábla néhány mezőjén bábu áll. Egy bábut akkor vehetünk le a tábláról, ha annak sorában vagy oszlopában a mezőknek legalább a fele üres. Legalább hány bábura van szükségünk ahhoz, hogy azokat alkalmasan elhelyezve egyiküket se lehessen levenni?
(3 pont)
B. 4393. Egy szabályos háromszögnek kiválasztottuk a csúcsait, a középpontját és az oldalainak harmadolópontjait. Hány pontot tarthatunk meg közülük úgy, hogy semelyik három ne alkosson szabályos háromszöget?
Javasolta: Demeter Albert (Matlap, Kolozsvár)
(4 pont)
B. 4394. Tekintsük az F1=F2=1, Fn=Fn-1+Fn-2 rekurzióval definiált Fibonacci-sorozatot. Bizonyítsuk be, hogy k<m esetén
összetett szám.
Javasolta: Lenger Dániel (Budapest)
(4 pont)
B. 4395. Adott egy húrnégyszög. Szerkesszünk minden oldal belsejében egy-egy pontot úgy, hogy az ezek által meghatározott konvex négyszög kerülete a lehető legkisebb legyen.
(5 pont)
B. 4396. Az ABC háromszög beírt köre a b oldalt F-ben, az a oldalt G-ben érinti. Igazoljuk, hogy az A-ból a  szög felezőjére állított merőleges talppontja rajta van az FG egyenesen.
szög felezőjére állított merőleges talppontja rajta van az FG egyenesen.
(3 pont)
B. 4397. Igazoljuk, hogy ha n, k pozitív egész számok, akkor
osztható n-nel.
Javasolta: Korándi Dániel (Budapest)
(3 pont)
B. 4398. Adott az ABC hegyesszögű háromszög BC oldalán az A1 pont, a CA oldalán a B1 pont, és az AB oldalán a C1 pont. Az AC1B1 körön jelöljünk ki egy A2 pontot. Legyen a C1A2 egyenes és a BA1C1 kör C1-től különböző metszéspontja B2, továbbá legyen az A1B2 egyenes és a CB1A1 kör A1-től különböző metszéspontja C2. Igazoljuk, hogy az A2, B1 és C2 pontok egy egyenesre esnek.
(4 pont)
B. 4399. Egy zsákban k db piros és n db zöld golyó van. Egyesével, visszatevés nélkül húzzuk ki a golyókat, és az első piros után megállunk. Átlagosan hányadik húzásnál következik ez be?
Javasolta: Maróti Gábor
(4 pont)
B. 4400. Bele lehet-e tenni az egységkockába egy 1,05×1,05-ös négyzetet?
(4 pont)
B. 4401. Legyen p=3n+1 prímszám. Adhatnak-e az számok páronként különböző maradékot p-vel osztva?
(5 pont)
 |
A-jelű feladatokA beküldési határidő 2011. december 12-én LEJÁRT. |
A. 545. Bizonyítsuk be, hogy ha a>b>1 egész számok, ab+1 osztható (a+b)-vel és ab-1 osztható (a-b)-vel, akkor .
Kolmogorov kupa, 2009
(5 pont)
A. 546. Igazoljuk, hogy
tetszőleges pozitív egész k esetén.
(5 pont)
A. 547. Adott az OA1A2A3 tetraéder mindegyik OAi élén egy Bi belső pont, az OAi él Ai-n túli meghosszabbításán pedig egy Ci pont (i=1,2,3). Tegyük fel, hogy az OAi+1Ai+2 és BiAi+1Ai+2 síkok által határolt hat lapú testbe, továbbá az BiAi+1Ai+2 és CiAi+1Ai+2 síkok által határolt testbe is egy-egy gömböt lehet írni. Bizonyítsuk be, hogy ekkor az OAi+1Ai+2 és CiAi+1Ai+2 síkok által határolt testbe is gömböt lehet írni.
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

