A KöMaL 2012. februári informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2012. március 12-én LEJÁRT. |
I. 286. Az alábbi játékban adott egy 4 sorból és 8 oszlopból álló terület, amelyet 8 darab, különböző alakú elemmel kell kitölteni, az egyes elemeket pontosan egyszer felhasználva. Az itt látható ábra egy lehetséges kitöltést ad meg. (A rajzzal az egyes elemek alakját is megadjuk.)

Természetesen ezen elemeket többféleképpen is elhelyezhetjük úgy, hogy a rendelkezésre álló területet pontosan kitöltsék. Az elemeket 90o-os fordulatokkal forgathatjuk vagy meg is fordíthatjuk, tehát mindegyik elemnek 8 helyzete lehet.
A játék során nem pusztán az üres területet kell kitöltenünk, hanem megadjuk az egyes elemek színét és a terület néhány helyén megszabjuk, hogy oda milyen színű résznek kell kerülnie.
Írjunk programot, amely megadja a darabok egy lehetséges elhelyezésének módját. A program első parancssori argumentuma az elhelyezendő darabok színét és a terület bizonyos helyeinek színét tartalmazó fájl neve, a második parancssori argumentum pedig a megoldást tartalmazó fájl neve. A programot csak olyan bemenetekkel teszteljük, amelyeknél van megfelelő elhelyezés.
A bemeneti állomány első sorában a nyolc elem (a rajzon megadott számsorrendben) színét adja meg, egymástól szóközzel elválasztva. A színt egyetlen karakter jelöli. A következő 4 sor a területet adja meg, soronként 8--8 karakterrel, amelyeket egymástól egy szóköz választ el. Amennyiben egy hely színe kötött, ott a színt jelölő karakter van, egyébként a * szerepel.
A kimeneti állomány a kitöltött téglalapot írja le. Pontosan 4 sort tartalmaz, soronként 8, egymástól szóközzel határolt számmal. A számok az elem sorszámát adják.
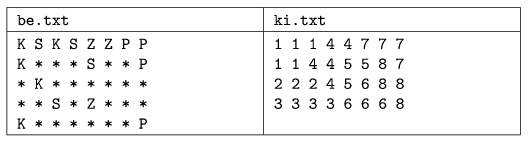
Beküldendő egy tömörített i286.zip állományban a program forráskódja (i286.pas, i286.cpp, ...), valamint a program dokumentációja (i286.txt, i286.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
(10 pont)
I. 287. Egy egész napos, hosszú túrára indulva érdemes az útvonalat részletesen megtervezni. Túratársaink sokfajta információra lehetnek kíváncsiak.
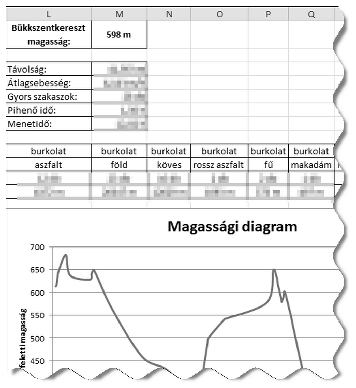
A Bükkszentkereszt és Eger közötti kiránduláshoz a túraútvonalat térképről és útvonaltervező programból származó adatokból jelöljük ki. A forrásállományban rendelkezésre állnak az útvonal egyes szakaszaira a turistajelzések betűjelei, a burkolatuk anyagainak nevei, a hosszúságuk, az emelkedésük és a süllyedésük méterben, valamint a megtételükhöz tervezett idő percben. (Az adatok forrása a http://turistautak.hu/ oldal.)
Táblázatkezelő program segítségével oldjuk meg a következő feladatokat:
1. Töltsük be a tabulátorokkal tagolt, UTF-8 kódolású utterv.txt. szövegfájlt a táblázatkezelőbe az A1-es cellától kezdődően. Munkánkat i287 néven mentsük el a táblázatkezelő alapértelmezett formátumában.
2. Oszlopok beszúrásával és a fejléc kiegészítésével hozzuk létre a minta szerinti táblázat szerkezetet.
3. Az E oszlopban határozzuk meg az indulástól méterben mért távolságot. A J oszlopban számoljuk ki az egyes szakaszokon várható sebességet a hossz és tervezett idő értékekből km/h mértékegységben.
4. A H oszlopban számoljuk ki az egyes szakaszok megtétele utáni tengerszint feletti magasságokat, ha a kiindulási (Eger) magasság értékét az M1 cella tartalmazza.
5. Az M3 cellában függvény segítségével határozzuk meg a gyalogtúra teljes hosszát kilométerben.
6. Az M4 cellában képlet segítségével határozzuk meg a túra átlagsebességét a teljes megtett út és az ehhez tervezett idők összege alapján.
7. Az M5 cellában írassuk ki, hogy hány olyan szakasz van, ahol a sebesség várhatóan a teljes átlagnál nagyobb lesz.
8. A túra során pihenőkre is szükség lesz. Az M6 cellában számítsuk ki, hogy hány órát tervezünk pihenésre fordítani, ha minden megtett 5 km után 10 percet célszerű pihenni.
9. Az M7 cellában számoljuk ki órában a terv szerinti menetidőt, amely a szakaszok megtételéhez szükséges idők és pihenőidők összege.
10. Az L9 cellától jobbra és lefelé határozzuk meg a különböző burkolatú útszakaszok számát és hosszuk összegét másolható képlettel.
11. Formázzuk a táblázatot az alábbi leírás és a minta szerint:
a. Az első sor celláit igazítsuk középre vízszintesen és függőlegesen.b. Az első sorban található oszlopneveket és szövegeket állítsuk félkövér betűstílusúra.
c. Azokban a cellákban, ahol a számított értékek várhatóan nem egész számértékek, állítsuk be, hogy két tizedes jeggyel jelenjenek meg.
d. Az I2:I4 tartományban a számított értékeknek állítsunk be minta szerinti mértékegységet és két tizedes jegyet. Az L oszloptól jobbra minden számított érték mértékegységgel együtt jelenjen meg.
e. Az adatokat tartalmazó cellákat belül vékony, és az A1:J57 tartomány celláit kívülről vastag vonallal szegélyezze. Az első sort alul is keretezze vastag vonallal. A többi adatot ne szegélyezze.
12. Készítsünk PontXY típusú diagramot, mely függőleges tengelyén a tengerszint feletti magasságot méterben és vízszintes tengelyén a megtett út hosszát kilométerben adjuk meg.
a. A diagramon adjunk meg tengelycímeket és a skálákat állítsuk be úgy, hogy az ábrázolt adatok kitöltsék a rendelkezésre álló területet.b. A diagramnak ne legyen jelmagyarázata és a címének a ,,Magassági diagram'' szöveget írjuk.
Beküldendő egy tömörített i287.zip állományban a táblázatkezelő munkafüzet (i287.xls, i287.ods, ...), illetve egy rövid dokumentáció (i287.txt, i287.pdf, ...), amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma.
(10 pont)
I. 288. Az alábbi feladat két része közül csak az egyiket kell megoldanunk. A választásnál érdemes figyelembe venni, hogy
- van-e az iskolánkban olyan vezeték nélküli hálózat, amelynek vizsgálata tanulságos?
- milyen eszköz áll rendelkezésre? (telefon, netbook, notebook)
a) Iskolai WiFi térkép.
Egyre több intézményben, iskolában fedik le nemcsak a közösségi tereket, hanem a teljes területet vezeték nélküli hálózattal. Az egyes hozzáférési pontok által ellátott területek szükségképpen részben fedik egymást.
Készítsünk térképet az iskolánk WiFi hálózatáról. A rajz tartalmazza a hozzáférési pont helyét és legyen leolvasható, hogy az egyes helyeken mely hozzáférési pontok milyen sebességgel érhetők el. (A megoldáshoz ötletet meríthetünk vezeték nélküli hálózatokat kezelő programok felületéből, de akár turista térképekről is.) Készítsük el a WiFi hálózat szöveges ismertetését is (pl. mióta működik, milyen eszközöket használnak, kik vehetik igénybe, az azonosítás milyen módszerrel történik stb.)
Beküldendő a szöveges ismertetést, a térképet, a mérési eszközt és a mérés módszerét bemutató i288.pdf dokumentum.
b) Utcai WiFi térkép.
Egyre több cég és magánszemély üzemeltet WiFi hozzáférési pontot. Ha végigsétálunk egy belvárosi utcán, lépésről-lépésre tűnnek fel újabb hozzáférési pontok.
Készítsünk térképet, amely grafikusan szemlélteti az út mentén elérhető hozzáférési pontokat. A mérés alapján készítsünk statisztikát, amely elemzi az SSID választási szokásokat (cégnév, személynév, véletlenszerű, gyári), a beállított csatornát és a biztonság típusát.
Beküldendő a térképet, a statisztikai adatokat és az azokból levont következtetéseket valamint a mérési eszközt és a mérés módszerét bemutató i288.pdf dokumentum.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2012. március 12-én LEJÁRT. |
S. 69. Egy N hosszúságú szövegben szeretnénk összesen K darab, egyenként M hosszúságú minta előfordulását megtalálni, azonban a minták betűi sajnálatos módon összekeveredtek. Feladatunk tehát az így összekeveredett minták egy-egy permutációját megtalálni a szövegben.
A program a feladat leírását a standard bemenetről olvassa. Ennek első sorában egy-egy szóközzel elválasztva három egész szám található, sorra N, M és K értéke (, 1
 M
M 1000,
1000, ). A második sorban az N hosszúságú szöveg szerepel, az ezt követő K darab sor pedig rendre az összesen K darab M hosszúságú mintát tartalmazza. Minden szöveg kizárólag az angol ábécé 26 kisbetűjéből áll.
A standard kimenetre írt megoldás összesen K sorból álljon, az i-edik sorba az a legkisebb pozíció kerüljön, amelytől kezdődően a N hosszúságú szövegben az i-edik minta egy tetszőleges permutációja megjelenik, vagy a 0 szám, ha nincs ilyen pozíció.

Beküldendő egy tömörített s69.zip állományban a program forráskódja (s69.pas, s689.cpp, ...) az .exe és más fordító által generált állományok nélkül, valamint a program rövid dokumentációja (s69.txt, s69.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrás melyik fejlesztő környezetben fordítható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.