A KöMaL 2013. januári matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2013. február 11-én LEJÁRT. |
K. 361. A delet egy digitális óra 12:00 alakban mutatja. Ezt értelmezzük négyjegyű számként: 1200. Hasonló módon értelmezzük a dél és éjfél közötti (óra:perc alakban kijelzett) időpontokat is négyjegyű számokként. Mennyi az összege az órán 12:00-től 23:59-ig látható négyjegyű számoknak?
(6 pont)
K. 362. Péter egy munkát 5 óra alatt végez el egyedül, Pál pedig 6 óra alatt. Ha együtt dolgoznak, akkor veszekednek, akadályozzák egymást, ezért munkatempójuk mindkettőjüknek azonos arányban csökken. Hány %-kal romlik a munkatempójuk, ha ketten együtt 3,5 óra alatt végzik el a munkát?
(6 pont)
K. 363. A Big Ben minden egész óra elteltét annyi ütéssel jelzi, ahány óra van. Ilyenkor az ütés után még egy ideig halljuk az ütés hangját, és a hallott ütések között szünetek vannak. Ha a Big Ben 9 másodperc alatt üti el a három órát, és 10,5 másodperccel több idő alatt az 5 órát, mint a 2 órát, akkor naponta összesen hány másodpercig halljuk az ütések hangját?
(6 pont)
K. 364. Egy téglatest alakú fadarab egyik élének hossza 10 cm. Az oldallapok irányára merőlegesen átmarjuk a téglatestet, mindhárom irányban egy-egy 2 cm alapélű négyzetes hasáb alakú lyukat készítve. (A furatok nem találkoznak egymással.) A 10 cm-es éllel párhuzamosan a harmadik furatot készítettük. Az első fúrás után a téglatest felszíne 32 cm2-rel nőtt, a második fúrás után a már kifúrt téglatest felszíne 15,92%-kal lett nagyobb. Mennyi lett a három lyuk kifúrása után kapott test térfogata?
(6 pont)
K. 365. Az ABC szabályos háromszög AC oldalának A-n túli meghosszabbításán levő D pontnak az AB egyenestől vett távolsága 4 egység, a BC egyenestől vett távolsága pedig 10 egység. Mennyi az ABC háromszög területe?
(6 pont)
K. 366. Mekkora az a legnagyobb összeg, amit nem lehet kidobni a képen látható darts-táblán, akárhányszor is dobhatunk rá?
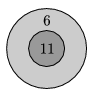
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2013. február 11-én LEJÁRT. |
C. 1150. Egy kockás papírra páratlan darabszámú kisnégyzetből álló négyzetet rajzoltunk. A rácsegyenesek mentén olyan zárt töröttvonalat szeretnénk rajzolni, amely minden, a négyzet belsejében és határvonalán lévő rácsponton áthalad pontosan egyszer, és nem lép ki a négyzetből. Adjuk meg a töröttvonal hosszát a nagy négyzet oldalhosszával.
(5 pont)
C. 1151. Az ABCD konvex négyszög egy tetszőleges belső P pontját kössük össze rendre a négyszög AB, BC, CD, DA oldalának E, F, G, H felezőpontjával. Igazolandó, hogy az AEPH és CGPF (esetleg elfajuló) négyszögek területének összege egyenlő a BFPE és DHPG (esetleg szintén elfajuló) négyszögek területének összegével.
Javasolta: Gyimesi Róbert (Budapest)
(5 pont)
C. 1152. Legyen
és
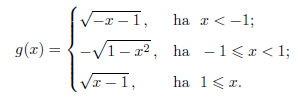
Adjuk meg f-g zérushelyeit.
(5 pont)
C. 1153. Egy egységnyi átlójú négyzetet egyik átlója mentén elvágunk, majd a másik átló egyenese mentén a két részt egymás felé toljuk. Legfeljebb mekkora területű közös rész jöhet létre?
(5 pont)
C. 1154. Van-e olyan számtani sorozat, amelyben az első n tag összege n, az első 2n tag összege n2 és az első 3n tag összege n3?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2013. február 11-én LEJÁRT. |
B. 4502. Egy zsákban 2013 korong van, megszámozva 1-től 2013-ig. Hányat kell közülük visszatevés nélkül kihúznunk, hogy biztosan legyen köztük két olyan szám, amelyek összege osztható 7-tel?
Javasolta: Fülöp Dóra (Pécs)
(3 pont)
B. 4503. Határozzuk meg azokat a négyjegyű négyzetszámokat, amelyeknek két első és két utolsó számjegye egyenlő.
(3 pont)
B. 4504. Egy derékszögű háromszögben az átfogó felezőmerőlegesének a befogók egyenesei közé eső szakasza ugyanolyan hosszú, mint az átfogó. Mekkorák a háromszög szögei?
(4 pont)
B. 4505. Van egy p és egy q literes edényünk. A vízcsapnál bármelyik edényt színültig megtölthetjük vagy kiüríthetjük, bármelyik edényből a másik edényt teletölthetjük, illetve bármelyik edény teljes tartalmát átönthetjük a másik edénybe. Bizonyítsuk be, hogy ha p>q egymáshoz relatív prím pozitív egészek, s pedig olyan pozitív egész, amelyre s p, akkor elérhetjük azt, hogy az egyik edényben pontosan s liter víz legyen.
p, akkor elérhetjük azt, hogy az egyik edényben pontosan s liter víz legyen.
Javasolta: Holló Gábor
(5 pont)
B. 4506. Igazoljuk, hogy létezik végtelen sok pozitív egész szám úgy, hogy közülük semelyik véges soknak az összege nem négyzetszám.
Javasolta: Kutas Péter
(4 pont)
B. 4507. Egy szabályos hétszög területe 4095 egység. A sokszög két szomszédos csúcsa A és B, a középpontja K. Az ABK háromszög körülírt körén, a hétszög belsejében fekvő P pontra
Mekkora lehet az ABP háromszög területe?
Olasz versenyfeladat
(5 pont)
B. 4508. Mutassuk meg, hogy ha a, b és c pozitív számok, akkor
Jim Boyd (USA) nyomán
(4 pont)
B. 4509. Két parabola tengelye merőleges egymásra. Mutassuk meg, hogy a két görbe közös pontjai egy körvonalra illeszkednek.
Javasolta: Holló Gábor (Budapest)
(5 pont)
B. 4510. Az O középpontú szabályos (2k+1)-szög alapú egyenes gúla alapéleinek hossza 1, OB magasságának hossza pedig m. Tükrözzük a gúlát az OB szakasz felezőpontjára. Mekkora a két gúla közös részének a térfogata?
(6 pont)
B. 4511. A k kör a P pontban belülről érinti az  kört. A P-n átmenő p egyenes ezeket a köröket P-n kívül még rendre a K és L pontokban metszi. A k kör egy P-től különböző U pontjában húzott u érintőjének az
kört. A P-n átmenő p egyenes ezeket a köröket P-n kívül még rendre a K és L pontokban metszi. A k kör egy P-től különböző U pontjában húzott u érintőjének az  körrel való egyik metszéspontja V, a KU és LV egyenesek metszéspontja pedig T. Határozzuk meg a T pont mértani helyét, ha U befutja k-t. (u és
körrel való egyik metszéspontja V, a KU és LV egyenesek metszéspontja pedig T. Határozzuk meg a T pont mértani helyét, ha U befutja k-t. (u és  mindkét metszéspontja figyelembe veendő; ha U=K, akkor a KU egyenes a k-hoz K-ban húzott érintő. Hasonlóan, ha V=L, akkor LV az
mindkét metszéspontja figyelembe veendő; ha U=K, akkor a KU egyenes a k-hoz K-ban húzott érintő. Hasonlóan, ha V=L, akkor LV az  -hez L-ben húzott érintő.)
-hez L-ben húzott érintő.)
Javasolta: Hraskó András (Budapest)
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2013. február 11-én LEJÁRT. |
A. 578. Minden n 2 egészre legyen P(n) az összes
2 egészre legyen P(n) az összes
alakú kifejezés szorzata, ahol az egyes tagok előjelét tetszőlegesen megválaszthatjuk.
(a) Bizonyítsuk be, hogy P(n) pozitív egész.
(b) Bizonyítsuk be, hogy tetszőleges  >0-hoz van olyan n0, hogy n>n0 esetén P(n) minden prímosztója kisebb, mint
>0-hoz van olyan n0, hogy n>n0 esetén P(n) minden prímosztója kisebb, mint .
(5 pont)
A. 579. A k1 kör belülről érinti a k kört, ami kívülről érinti a k2 kört. A k1 és k2 külső közös érintői u és v. Az u egyenes k1-et a P, k2-t a Q pontban érinti, a k kört pedig A-ban és B-ben metszi úgy, hogy a B metszéspont esik a PQ szakaszra. Hasonlóan, a v egyenes k1-et az R, k2-t az S pontban érinti, k-t pedig C-ban és D-ben metszi úgy, hogy a D pont esik az RS szakaszra, és k1 az A-t és C-t nem tartalmazó BD ívet érinti.
Mutassuk meg, hogy
(5 pont)
A. 580. Mutassuk meg, hogy minden k pozitív egészhez és  >0 valós számhoz van olyan valós együtthatós
>0 valós számhoz van olyan valós együtthatós polinom, amelyre p(x) osztható az (x-1)k+1 polinommal, és
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

