A KöMaL 2013. májusi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2013. június 10-én LEJÁRT. |
I. 322. Kiránduláskor és más társas összejövetelkor kellemes időtöltés, illetve agytorna a szójáték. Általában a szójáték magyarázatához példákat szoktunk adni. Az alábbiakban szójátékokhoz egy adott szókészletből példákat, illetve megoldásokat gyűjtünk ki.
A feladatok megoldásához rendelkezésre áll a honlapunkról letölthető szoveg.txt fájl, amelybe Gárdonyi Géza: Egri csillagok című regényéből gyűjtöttünk ki szavakat. Az állományban csak olyan szavak szerepelnek, melyek az angol ábécé betűivel leírhatók. A könnyebb feldolgozhatóság érdekében minden szó csupa kisbetűvel szerepel, szavanként külön sorban. Tudjuk, hogy ebben az állományban a szavak 20 karakternél nem hosszabbak.
Készítsünk programot i322 néven, amely az alábbi problémákat oldja meg, a parancssor argumentumaként megadott szoveg.txt állományban talált szavak felhasználásával. A feladatot úgy oldjuk meg, hogy tetszőleges hosszúságú szövegállomány esetén működjön.
Minden - képernyőre írást igénylő - részfeladat megoldása előtt írjuk a képernyőre a feladat sorszámát. Ha a felhasználótól kérünk be adatot, jelenítsük meg a képernyőn, hogy milyen értéket várunk (például az 1. feladat esetén: ,,1. feladat Adjon meg egy szót: ''). Az ékezetmentes kiírás is elfogadott. A feladatok eredményének képernyőre írásánál - ha más előírás nincs - a szavakat egy-egy szóköz válassza el.
1. Kérjünk be a felhasználótól egy szót, és döntsük el, hogy csak egyféle magánhangzót tartalmaz-e. Amennyiben egyfélét tartalmaz, írjuk ki, hogy ,,Csupa azonos magánhangzó van benne'', ha nincs vagy többféle van benne, akkor írjuk ki, hogy ,,Az állítás hamis''. A begépelendő szóról feltételezhetjük, hogy csak az angol ábécé kisbetűit tartalmazza. Az angol ábécé magánhangzói: a, e, i, o, u.
2. Írjuk ki a képernyőre, hogy a szoveg.txt állományban hány mély, magas és vegyes hangrendű szó van. Mély hangrendű egy szó, ha benne csak a, o, u található; magas hangrendű, ha csak e, i; végül vegyes hangrendű, ha az előző két felsorolásból vegyesen vannak magánhangzók. A darabszámok után írjuk ki, hogy ezek hány százalékát teszik ki az összes szónak. A százalékot két tizedessel jelenítsük meg.
Például:
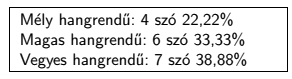
3. Kérjünk be a felhasználótól egy szórészletet (egybefüggő karaktersorozatot), amely maximum 20 karakterből állhat, és gyűjtsük ki azokat a szavakat, amelyek ezt tartalmazzák. Ezeket a szavakat írjuk ki a képernyőre.
4. Gyűjtsük ki és írjuk a képernyőre azokat a szavakat, amelyekben a betűk ábécé sorrendben vannak.
Például:

5. Válogassuk ki azokat a szavakat, amelyek első és utolsó betűjét elhagyva a szoveg.txt állományban szereplő új, értelmes szót kapunk.
6. Keressünk a szókészletben és írjunk ki 10 darab ál-ikerszót, amelyek eleje a szó második részében megismétlődik, azaz a szó első fele egyezik a második felével.
Például:

7. Hozzunk létre egy kettevag.txt állományt, amelybe gyűjtsünk ki a szókészletből 100 darab olyan szót, amelyet kettévágva két másik, a szoveg.txt állományban szereplő értelmes szót kapunk. A kiírásnál minden szó külön sorba kerüljön.
Például:

Beküldendő egy tömörített i322.zip állományban a program forráskódja (i322.pas, i322.cpp, ...), valamint a program rövid dokumentációja (i322.txt, i322.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
Letölthető fájl: szoveg.txt
(10 pont)
I. 323. A debreceni villamos tanítási időszak alatti menetrendje alapján utastájékoztató szolgáltatást szeretnénk készíteni. A honlapunkról letölthető a debreceni 1-es villamos menetrendjét tartalmazó menetrend.txt fájl (tabulátorokkal tagolt, UTF-8 kódolású szövegállomány).
Nyissuk meg táblázatkezelő program segítségével a menetrend.txt fájlt úgy, hogy az első beolvasott adat az A1-es cellába kerüljön. A táblát mentsük a táblázatkezelő saját formátumában i323 néven.
A munkafüzet menetrend munkalapján az A oszlopban a körjáratban üzemelő villamos Nagyállomás végállomásáról induló szerelvények indulási idői, a C oszlopban a megállók nevei és a D oszlopban az állomások közötti menetidők vannak.
Az E oszlopban számoljuk ki a Nagyállomástól mért menetidőket a minta szerinti formátumban. A körjárat miatt azonos nevű megállók vannak a táblázatban.
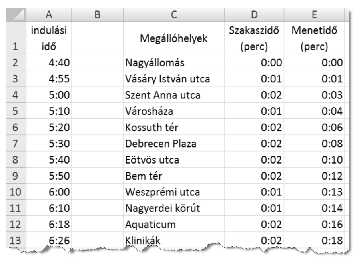

A tájékoztató adatoknak - a mintán már nem látható - E oszlopban kell megjelenniük, a B1:B3 cellákban megadott adatok alapján.
A megoldás során a G oszloptól jobbra végezhetünk segédszámításokat, amelyeket lássunk el magyarázó szöveggel.
Az E1 cellában a helyes vagy helytelen felirat jelenjen meg a B1:B3 cellákban lévő paraméterek használhatósága alapján. Értelem szerint helytelen a felirat, ha nem létező megállóneveket, vagy ha a szerelvény végállomásról induló időpontja üzemidőn kívüli lenne, vagy ha egyéb hibás adatot adunk meg. Igyekezzünk minél több hibát kiszűrni és ezeket a segédszámítás területén dokumentálni. A helytelen felirat megjelenése esetén a további információs cellákban ne jelenjen meg semmi.
Az E2 cellában jelenítsük meg a villamos menetrendszerinti pontos érkezési idejét, amelyre az utas a cél irányába először felszállhat. (Egyszer talán a valóságban is így lesz.)
Az E3 cellában határozzuk meg, hogy a célállomásra mikor érkezik meg a villamos.
Az E4 és az E5 cellában írjuk ki, hogy az utazás során hány megállót és mennyi menetidő alatt tesz meg a villamos.
Beküldendő egy tömörített állományban (i323.zip) a táblázatkezelő munkafüzet (i323.xls, i323.ods, ...), illetve egy rövid dokumentáció (i323.txt, i323.pdf, ...), amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziója, valamint a megoldás rövid leírása.
Letölthető fájl: menetrend.txt
(10 pont)
I. 324. Mutassuk be prezentáció segítségével a geometriai inverziót! Az inverzió témájában több kiváló írás is olvasható a neten, a témát sokszor feldolgozták középiskolás szakkörökön is, ezért úgy gondoljuk, hogy e matematikai téma megértése nem jelent gondot, sőt izgalmas lesz az informatikában versenyzőknek is. Készítsünk először egyet, amelyen bemutatjuk az inverzió fogalmát és tulajdonságait, valamint egy másikat, amelyen animáció segítségével megmutatjuk, hogyan szerkeszthető meg csak körző segítségével egy pont inverz képe. A harmadik dián mutassuk be, miként szerkeszthető meg pl. egy kör inverz képe. A szerkesztéseknél a GeoGebra programot használjuk, amely a szerkesztést lépésenként levetítve is meg tudja mutatni. Vegyük föl a programból az animációt, vagy az egyes állapotok képéből szerkesszük meg azt a bemutatókészítő programmal, vagy más animációkészítő alkalmazásban. A következő diákon mutassuk be az inverzió módszerének hatékonyságát egy olyan szerkesztési feladaton, amelynél csak körző használható az euklideszi szerkesztéshez. Mutassuk be a megoldás menetét úgy, hogy az euklideszi szerkesztés lépéseit és az inverzióval való szerkesztés lépéseit egyszerre, szinkronban lehessen az adott dián látni.
Beküldendő egy i324 tömörített mappában a prezentáció (i324.ppt, i324.odp, ...), valamint egy rövid dokumentáció (i324.txt, i324.pdf, ...), amely megadja, hogy a bemutató melyik prezentációkészítő szoftver hányas számú verziójával készült.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2013. június 10-én LEJÁRT. |
S. 81. Egy házat szeretnénk felépíteni, ahol ismertek a munkafázisok (pl. üvegezés, villany bevezetése, vakolás stb.). Az építési munkákról ismert, hogy egyes feladatok elkezdése után legalább mennyi időnek kell eltelnie, amikortól bizonyos más feladatokat elkezdhetünk (pl. a villany bevezetése előtt meg kell építeni a falakat, ami x nap). Egyszerre akár több munkafázison is dolgozhatunk. A ház építéséhez bérelnünk kell eszközöket az utolsónak elkezdett munkafázis első napjáig, mivel feltehetjük, hogy a legutolsó munkafázis egy nap alatt befejezhető. Tehát ha a T. napon kezdünk el utoljára munkafázist, akkor összesen T.P forint bérleti díjat kell fizetni. Az alapanyagok megvásárlása következtében minden munkafázis további költségeket jelent. A mostani feladatban úgy tekintjük, hogy az alapanyagok ára monoton csökken (azaz későbbi időpontban sosem lesz nagyobb, mint egy korábbi esetén lenne), és intervallumonként konstans. (Vagyis pl. 1-10. napig 30 forint, 11-20. napig 20, utána 21-40. napig 15 forint.)
Írjunk programot, amely a feladatok egymásra épülése, a P bérleti díj, illetve az egyes feladatokhoz szükséges intervallumonkénti alapanyagárak ismeretében megadja, hogy minimum mennyi pénzbe kerül a ház fölépítése, ha a lehető legügyesebben ütemezzük az egyes feladatok elkezdését.
A standard bemenet első sorában található a feladatok N, illetve az egymásra épülések E száma, valamint a P bérleti díj (,
, 0
 P
P 1000) szóközökkel elválasztva. A következő E sor mindegyikében három szám található, példaként (ai,bi,ci), amelyek egymásra épüléseket írnak le: az ai sorszámú munka megkezdése után ci nappal lehet elkezdeni a bi sorszámú munkát (1
1000) szóközökkel elválasztva. A következő E sor mindegyikében három szám található, példaként (ai,bi,ci), amelyek egymásra épüléseket írnak le: az ai sorszámú munka megkezdése után ci nappal lehet elkezdeni a bi sorszámú munkát (1 i
i E). A következő N sor az egy-egy munkához szükséges alapanyagok árainak alakulását tartalmazza a következőképpen: az első szám K (1
E). A következő N sor az egy-egy munkához szükséges alapanyagok árainak alakulását tartalmazza a következőképpen: az első szám K (1 K
K 100), és ezután K darab egymáshoz illeszkedő intervallum leírása következik két-két számmal (fj,vj), melyek jelentése: az intervallumon fj forintba kerül megvenni az alapanyagokat az adott munkához, és a vj-edik nap az intervallum utolsó napja (azaz amikor még fj forintba kerül a vásárlás) (0
100), és ezután K darab egymáshoz illeszkedő intervallum leírása következik két-két számmal (fj,vj), melyek jelentése: az intervallumon fj forintba kerül megvenni az alapanyagokat az adott munkához, és a vj-edik nap az intervallum utolsó napja (azaz amikor még fj forintba kerül a vásárlás) (0 fj
fj 1000, 1
1000, 1 vj
vj 109). Az első intervallum az 1. napon indul, a továbbiak pedig mindig az előző intervallum vége utáni napon kezdődnek (1
109). Az első intervallum az 1. napon indul, a továbbiak pedig mindig az előző intervallum vége utáni napon kezdődnek (1 j
j K).
K).
A standard kimenet egyetlen sorába írjuk ki a ház fölépítésének minimális költségét.
Feltehetjük, hogy az egymásra épülésekből nem következik ellentmondás, vagyis a ház mindenképpen felépíthető. Az egyes feladatokhoz szükséges alapanyagokat a feladat elkezdésének napján kell megvennünk. Az utolsó árintervallumok minden feladatnál ugyanazon a D. napon végződnek (1 D
D 109). Az építkezést leghamarabb az 1. napon kezdhetjük, és be kell fejeznünk legkésőbb a D. napon.
109). Az építkezést leghamarabb az 1. napon kezdhetjük, és be kell fejeznünk legkésőbb a D. napon.

Magyarázat a példához: Egy optimális építési tervben pl. a következőek lehetnének az elkezdési idők: 1, 2, 4, 8 vagy 1, 2, 3, 8. Ekkor az alapanyag beszerzések költsége 3+2+3+3=11, és ehhez jön még 8 Ft bérleti díj, vagyis az összköltség 19. (Ha az elkezdési idők pl. 1, 2, 3, 7 lennének, akkor az összköltség 3+2+3+10+7=25 lenne.)
Értékelés: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a maximális 9 pont, ha bármilyen, a feltételeknek megfelelő tesztesetet képes megoldani 1 mp futásidőkorláton belül. A megoldásra részpontszám kapható, ha a program csak a maximális bemeneti számoknál nagyságrendekkel kisebb tesztesetekre tud lefutni időben (pl. kisebb N, E, vj, vagy K).
Beküldendő egy tömörített s81.zip állományban a program forráskódja (s81.pas, s81.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, a program rövid dokumentációja (s81.txt, s81.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

