A KöMaL 2013. decemberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2014. január 10-én LEJÁRT. |
M. 337. Szappanbuborék esési sebességét mérve adjunk becslést a buborék falvastagságára!
Varga István (1952-2007) feladata
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2014. január 10-én LEJÁRT. |
P. 4583. Egy sportkocsi fékezésekor 290 m hosszú féknyomot hagyott. Csúszása közben egészen a megállásig állandó erő fékezte, 3,90 m/s2 lassulással. Milyen sebességgel haladt az autó, amikor megcsúszott? Mekkora erő fékezte? Mekkora volt az úttest és a gumik között a súrlódási együttható? Az autó tömege megtankolva, sofőrrel együtt 2150 kg.
Tornyai Sándor fizikaverseny, Hódmezővásárhely
(3 pont)
P. 4584. Jancsi és Juliska álma, hogy az űrben fognak összeházasodni. Az űrállomáson a ceremónia végén egymás mellett lebegnek nyugalomban, de 10 cm híján nem érik el egymást. Kb. mennyi ideig kell várniuk, hogy a gravitáció hatására elérjék egymást? Hogyan tudnák lerövidíteni ezt az időt? (A szükséges adatokat becsüljük!)
Közli: Vass Miklós, Budapest
(4 pont)
P. 4585. Egy M és egy m tömegű kis golyót közös pontban felfüggesztett,  hosszúságú fonalakhoz rögzítünk. Vízszintesig kitérítjük, majd egyszerre elengedjük a golyókat, amelyek ezután centrálisan, tökéletesen rugalmasan ütköznek.
hosszúságú fonalakhoz rögzítünk. Vízszintesig kitérítjük, majd egyszerre elengedjük a golyókat, amelyek ezután centrálisan, tökéletesen rugalmasan ütköznek.
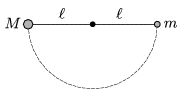
a) Milyen M/m tömegarány esetén jut el a m tömegű golyó a fonál által lehetővé tett legnagyobb magasságig az első ütközés után?
b) Milyen magasra jut el ebben az esetben a M tömegű test?
Közli: Kiss Miklós, Gyöngyös
(4 pont)
P. 4586. Egy négyzet alakú, egyenletes tömegeloszlású szőnyeget az egyik sarka körül teljes felületével a padlón csúsztatva 360o-kal elforgatunk. A csúszási súrlódási együttható mindenhol ugyanakkora a padlón. Ugyanekkora munkával ugyanezt a szőnyeget hányszor tudnánk a középpontja körül csúsztatva teljesen körbeforgatni?
Közli: Gáspár Merse Előd, Budapest
(5 pont)
P. 4587. Egy függőleges, rögzített rúdon fel-le mozoghat egy pontszerűnek tekinthető m tömegű test. A test közepén függőleges furat található, ezen megy át a rúd, ami a test számára súrlódásmentes mozgást biztosít. A testhez két könnyű, vékony fonál csatlakozik, melyek kezdetben  =45o-os szöget zárnak be a függőlegessel. A fonalak azonos magasságban lévő, rögzített csigákon haladnak át, a végükre M=1 kg tömegű testeket rögzítettünk. A rendszert nyugalmi állapotból indítjuk el.
=45o-os szöget zárnak be a függőlegessel. A fonalak azonos magasságban lévő, rögzített csigákon haladnak át, a végükre M=1 kg tömegű testeket rögzítettünk. A rendszert nyugalmi állapotból indítjuk el.
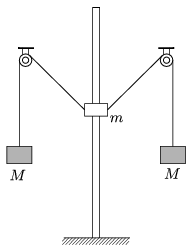
a) Mekkora a rúdon mozgó test m tömege, ha az elengedést követően éppen olyan magasságban áll meg, amikor a hozzá rögzített fonalak vízszintes helyzetűek?
b) Mekkora gyorsulással indul el visszafelé a m tömegű test, és mekkora gyorsulással indulnak el visszafelé a M tömegű testek?
Közli: Honyek Gyula, Budapest
(4 pont)
P. 4588. Az a oldalélű, m tömegű, homogén tömegeloszlású kockát egy érdes felületű, sík tartóra helyezzük, és az egyik oldaléle mentén egy kicsiny ütközőhöz illesztjük. A tartót fonalakkal felfüggesztjük a kocka tömegközéppontja felett magasságban (lásd az ábrát), majd a rendszert ingaként bizonyos szöggel óvatosan kitérítjük, és ott elengedjük.
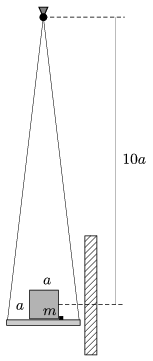
Amikor az inga legmélyebb helyzetébe visszaérkezik, a sík tartó egy nagy tömegű falba ütközik. Mekkora volt a kitérítés szöge, ha a kocka átborul az ütközőn? Az ütközések tökéletesen rugalmatlanok.
(A tartó és a fonalak tömege a kocka tömege mellett elhanyagolható. A kocka tehetetlenségi nyomatéka a középpontján átmenő bármely tengelyre ma2/6.)
Közli: Gnädig Péter, Vácduka
(5 pont)
P. 4589. Becsüljük meg, milyen messze vannak egymástól a H2O molekulák
a) 0 oC-os vízben;
b) 0 oC-os jégben;
c) 0 oC-os levegőben, 100%-os páratartalom esetén.
Közli: Radnai Gyula, Budapest
(4 pont)
P. 4590. Hőszigetelő hengerben ugyancsak hőszigetelő, könnyen mozgó dugattyú választ el 12 l és 8 l térfogatú, normál állapotú levegőt. A 8 l térfogatú részbe fűtőszálat építettünk, amellyel a gáz hőmérsékletét 200 oC-ra emeljük, majd a fűtést kikapcsoljuk.
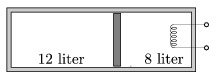
a) Mekkora a két gáz térfogata és nyomása a folyamat végén?
b) Mekkora az eredetileg 12 l térfogatú levegő hőmérséklete a folyamat végén?
c) Mennyi hőt vesz fel a melegített gáz a folyamat végéig?
d) Mennyivel változik a két gáz belső energiája külön-külön?
Közli: Holics László, Budapest
(5 pont)
P. 4591. Egy L élhosszúságú szabályos tetraéder csúcsaiban 4 db m tömegű, pozitív töltésű, kisméretű golyót helyezünk el, amelyeket elhanyagolható tömegű, szigetelő fonalak kötnek össze. Három golyó töltése Q, a negyediké 2Q.
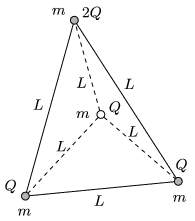
a) Egy adott pillanatban a 2Q töltésű golyót a többivel összekötő három fonalat egyszerre elvágjuk. Határozzuk meg a testek kezdeti gyorsulását az elvágás pillanatában!
b) Mekkora sebességre gyorsulnak fel a testek?
Közli: Kotek László, Pécs
(5 pont)
P. 4592. Vízszintes síkban két, egymással  szöget bezáró, elhanyagolható ellenállású vezető szál helyezkedik el. Rajtuk az
szöget bezáró, elhanyagolható ellenállású vezető szál helyezkedik el. Rajtuk az  szögfelezőjére merőlegesen, a vezető szálak A metszéspontjától x0 távolságban egy m tömegű, hosszegységenként r ellenállású, elegendően hosszú rúd fekszik, az ábrán látható módon. Az egész elrendezés függőleges irányú, homogén, B indukciójú mágneses térben található.
szögfelezőjére merőlegesen, a vezető szálak A metszéspontjától x0 távolságban egy m tömegű, hosszegységenként r ellenállású, elegendően hosszú rúd fekszik, az ábrán látható módon. Az egész elrendezés függőleges irányú, homogén, B indukciójú mágneses térben található.
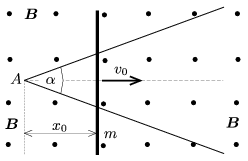
A rudat a szögfelező irányában v0 kezdősebességgel elindítjuk. A rúd és a vezető szálak között jó az elektromos kontaktus, de a súrlódás elhanyagolható.
Hol áll meg a rúd?
Közli: Simon Péter, Pécs
(5 pont)
P. 4593. Két részecske a fénysebességhez nagyon közeli (ultrarelativisztikus) sebességgel rugalmasan ütközik. A részecskék ütközés előtti impulzusvektorai az ábrán láthatók. Szerkesszük meg azt a legkisebb szöget, amelyet a szétrepülő részecskék mozgásiránya bezárhat egymással!
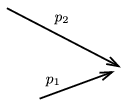
Közli: Vigh Máté, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

