A KöMaL 2014. januári informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2014. február 10-én LEJÁRT. |
I. 337. A jenga népszerű szórakoztató társasjáték, amelyet - kevésbé élvezetes formában - akár online is játszhatunk. A játékszabály elérhetősége http://tarsasoznijo.blog.hu/2009/04/14/jenga, az online játék elérhetősége http://hu.freeonlinegames.com/game/jenga.
Míg a valóságban nagy szerep jut az ügyességnek, a számítógépes változat inkább logikai játéknak tekinthető.
A klasszikus jenga játékkal szemben mi kezdésként n emeletből álló tornyot építünk. Az egyes emeletek felülnézetben felváltva mutatják az alábbi (A/B) szerkezetet:

A ledőlés vizsgálatához gondolatban minden jenga elemet bontsunk fel három négyzet alapú hasábra, ezek súlya legyen egységnyi. (Ilyen formában az emeletek közötti szerkezeti különbség eltűnne.) A torony egy hiányos emelet felett dőlhet le. A ledőléshez szükséges állapotot a feladatban úgy definiáljuk, hogy a hiányzó és meglévő elemek találkozásánál lévő ,,alátámasztási'' él hiányos oldalán nagyobb forgatónyomaték lép föl, mint a másikon. A ledőlés vizsgálatát szemlélteti a mellékelt oldalnézeti ábra. Az alsó szint hiányos, az alátámasztási élt ebben a képben a kis kör jelöli. Úgy tekintjük, hogy az egyes elemek tömege a tömegközéppontjukban van. Itt a hiányos oldalon 3 egység a forgatónyomaték (a nehézségi erő 6, az erőkar 0,5 egység), a másik oldalon 7,5 egység a forgatás mértéke (a középső oszlop felett a nehézségi erő 6, az erőkar 0,5 egység, a jobb oldali oszlop felett a nehézségi erő 3, az erőkar 1,5 egység), tehát itt nem dől le a torony. (A számításnál feltettük, hogy a középső szintről egy jenga elem sem hiányzik.)
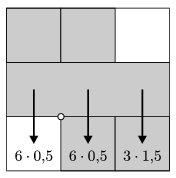
Írjunk programot, amely a hasábok mozgatás-sorozatát vizsgálva megállapítja, hogy melyik lépés eredményeként dől le a torony. A bemenet első sorában az emeletek száma található. Alatta soronként három adat szerepel egy-egy lépés leírásaként. Az első szám megadja, hogy melyik emeletről veszik el az elemet, a második az adott elem helyét írja le (1/2/3), a harmadik pedig az elhelyezés pozícióját (1/2/3) adja meg. A kimenet megadja a lépés sorszámát és a ledőlés okát: ,,az eltávolítás miatt'', ,,az elhelyezés miatt''.

A program első parancssori argumentuma a bemeneti fájl, a második pedig a kimeneti fájl neve legyen.
Beküldendő egy tömörített i337.zip állományban a program forráskódja (i337.pas, i337.cpp, ...), valamint a program rövid dokumentációja (i337.txt, i337.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
I. 338. Az atlétika női versenyei közül a legösszetettebb a hétpróba. A hétpróba hét versenyszáma: 100 m gátfutás, 200 m és 800 m futás, magasugrás, távolugrás, súlylökés és gerelyhajítás. A verseny pontozásos rendszerű. A versenyszámokat nemzetközi ponttáblázat alapján értékelik, amelyben minden elért eredménynek megvan a maga pontszáma.
A versenyszám pontszámának kiszámítására a következő képletet használják a versenyző x eredményét figyelembe véve:
pont=[a.|x-b|c]
(ahol [ ] a kifejezés egészrészét, | | az abszolút értékét jelenti).
Az a, b és c konstansok a Nemzetközi Atlétikai Szövetség által közölt, versenyszámonként eltérő konstansok.

Például: Farkas Györgyi magasugrásban 180 cm-ig jutott el, így ebben a versenyszámban 978 pontot ért el.
A 2012. évi nyári olimpiai játékok hétpróbázó versenyzőinek az egyes versenyszámokban elért eredményei és a pontszámításhoz szükséges adatok állnak rendelkezésünkre a versenyzo.txt, az eredmeny.txt, a vszam.txt és a nemzet.txt állományokban. Az állományok tabulátorral tagolt, UTF-8 kódolású szövegfájlok, az első sorok a mezőneveket tartalmazzák.
1. Készítsünk új adatbázist hetproba néven. A mellékelt adatállományokat importáljuk az adatbázisba a fájlnévvel azonos versenyzo, eredmeny, vszam és nemzet néven.
2. Beolvasáskor állítsuk be a megfelelő adatformátumokat és kulcsokat. A táblákba ne vegyünk fel új mezőt.
Táblák:


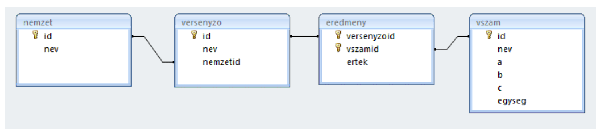
Készítsük el a következő feladatok megoldását. Az egyes lekérdezéseknél ügyeljünk arra, hogy mindig csak a kért értékek jelenjenek meg és más adatok ne. A megoldásainkat a zárójelben lévő néven mentsük el.
3. Lekérdezés segítségével adjuk meg, hogy ki nyerte a magasugrást. Az eredményben a versenyző nevét, eredményét és annak mértékegységét jelenítsük meg. (3magas)
4. Készítsünk lekérdezést, amely kilistázza a távolugrásban 1000 pontnál többet elérő versenyzők nevét, eredményét mértékegységgel együtt és pontszámát a mintának megfelelően. (4tavol)

5. A hétpróba versenyen nemzetenként többen is részt vehettek. Soroljuk fel a versenyzők száma szerint csökkenő sorrendben, hogy az egyes nemzetekből hány induló volt. (5nemzetdb)
6. Lekérdezés segítségével adjuk meg azoknak a versenyzőknek a nevét nemzeti azonosítójuk sorrendjében, akik mind a hét versenyszámban érvényes eredménnyel rendelkeztek. (6teljesek)
7. Soroljuk fel lekérdezés segítségével versenyszámonként az érvényes eredményt elért versenyzők számát. (7szamonkent)
8. Adjuk meg lekérdezés segítségével a magyar résztvevő eredményeit. A listában a versenyszám neve, az elért eredmény mértékegységgel együtt és az elért pontszám jelenjen meg. (8magyar)
9. Határozzuk meg a hétpróba verseny végeredményét. A listában csökkenő összpontszám szerinti sorrendben jelenjen meg a versenyző neve, nemzetének azonosítója és összpontszáma. (9vegeredmeny)
Beküldendő egy tömörített állományban (i338.zip) az adatbázis (hetproba.odb, hetproba.mdb, ...), valamint egy rövid dokumentáció (i338.txt, i338.pdf), amelyből kiderül az alkalmazott adatbázis-kezelő neve és verziószáma.
Letölthető fájlok:
(10 pont)
I. 339. A Prolog egy funkcionális programozási nyelv, melyben tényeket és logikai állításokat fogalmazhatunk meg. Ezek a formulák tartalmazhatnak konkrét adatokat és ismeretlen mennyiségeket. Például egyszerűen megfogalmazhatjuk, hogy melyik tanár, melyik napon és órában milyen tantárgyat tanít: tanít(kovács,fizika,szerda,4). A formulákban szereplő és kisbetűvel kezdődő szövegek konkrét tényeket, míg a nagybetűvel kezdődőek változót, ismeretlent jelentenek. Az állításokban szereplő ismeretlenek a program végrehajtása során kapnak értéket. A végrehajtás egy állítás igazságának a megkeresésével indul, melyet célállításnak hívunk. Ha például a célállítás a tanít(Ki,Mit,szerda,4), akkor a Prolog rendszer igaznak értékeli a tanít formulát úgy, hogy az ismeretlenek helyére Ki=kovács és Mit=fizika értékeket adja. A Prologról bővebben olvashatunk például Márkusz Zsuzsanna: Prologban programozni könnyű című könyvéből.
A Visual Prolog (ingyenesen letölthető és tanulásra használható a Personal Edition) Prolog programozási környezet, melynek PIE projektjében egyszerűen megfogalmazhatjuk állításainkat. A Visual Prologról és a PIE-ról bővebben olvashatunk a www.visual-prolog.com oldalon a Fundamental Visual Prolog #1 és #2 online tananyagban.
Prologban listák is használhatók, melyekkel a funkcionális nyelvekben megszokott műveletek végezhetők. Segítségükkel több információ is elhelyezhető egy tényállításban. Az alábbi lista feladatunk alapadatait tárolja, és azt mutatja meg, hogy az adott megoldást beküldő versenyző valamely KöMaL pontverseny adott számú feladatára hány pontot kapott:
pont( [ [kiss_tamás,i,330,5], [benedek_andrea,b,4500,0], ...,[kiss_tamás,i,340,10] ] ).
A lista alapján válaszoljunk a következő kérdésekre úgy, hogy elkészítjük a megadott nevű és paraméterű Prolog formulákat:
1. Hányan küldték be az I. 330. feladat megoldását - beküld_i330(DB)?
2. Hány nem 0 értékű megoldást küldtek be összesen a P pontversenyben - hány_nemnulla(P,DB)?
3. Hány pontot kaptak az egyes versenyzők a B. 4500. feladatra - pontok_b4500(V,Pont)?
4. Kik versenyeznek a C pontversenyben (az eredmény a nevek listája, amelyben minden név csak egyszer fordul elő) - kik_c(Lista)?
5. Melyik pontverseny melyik feladatának megoldásával szerezték a beküldő versenyzők összesen a legkevesebb pontot, és mennyit - legkevesebb(P,F,Pont)?
Beküldendő i339.pro néven egy a PIE rendszerben végrehajtható Prolog forrásprogram.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2014. február 10-én LEJÁRT. |
S. 86. Egy parkban azt látjuk, hogy N majom közül az 1-es számú egy nagyon nagy fa egyik ágába kapaszkodik a farkával. A majmok a kezükkel kapcsolódhatnak más majmokhoz úgy, hogy egy majom egy másik lábát fogja. Így tarthatnak más majmokat azáltal, hogy beléjük kapaszkodnak, vagy úgy, hogy beléjük kapaszkodnak más majmok. Egy majom lábába bárhány majom kapaszkodhat. Szeretnénk végezni egy M másodpercig tartó vizsgálatot, amelynél minden másodpercben egy majom szabaddá teszi adott kezét, vagyis elengedi egy másik majom lábát, ha eddig fogta azt. A program számítsa ki, hogy mikor esnek le az egyes majmok a földre. Egy majom akkor esik le, ha az 1-es számú majom nem tartja közvetett, vagy közvetlen módon.
A standard bemenet első sorában a majmok száma és a vizsgálat ideje
másodperc található, a következő N sor mindegyikében két szám (bi és ji), amely megadja, hogy az i-edik majom a bal és a jobb kezével hányadik majomba kapaszkodik. Amennyiben valamelyik szám -1, az azt jelenti, hogy azzal a kezével senkibe sem kapaszkodik, azzal a kezével senkit sem tart. A standard bemenet következő M sorában az xj, yj egészek megmutatják, hogy a j-edik másodpercben az xj-edik majom az yj-edik kezével elengedi a fogást (1. kéz a bal, 2. kéz a jobb). A program írja a standard output N sorába a majmok földet érésének idejét. Az i-edik sorba az i-edik majom földet érésének ideje kerüljön, és -1, ha nem ér földet a vizsgált időintervallum végéig.

Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani a beolvasástól számított 0.05 mp futásidőkorláton belül.
Részpontszámok a következőkre kaphatóak:
- a program N 100-ra megoldást ad;
100-ra megoldást ad;
- a program N 5000-re megoldást ad;
5000-re megoldást ad;
- a program -re megoldást ad.
Beküldendő egy tömörített s86.zip állományban a program forráskódja (s86.pas, s86.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, valamint a program rövid dokumentációja (s86.txt, s86.pdf, ...), amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

