A KöMaL 2014. decemberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2015. január 12-én LEJÁRT. |
M. 346. Gurítsunk el különböző vízszintes felületeken egy tömör hengert úgy, hogy mindvégig csúszásmentesen gördüljön! A mérési adatok alapján határozzuk meg, hogy mekkora csúszó súrlódási együtthatójú test mozogna forgásmentesen csúszva ugyanakkora gyorsulással, mint ahogy a gördülő henger középpontja.
Varga István (1952-2007) feladata
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2015. január 12-én LEJÁRT. |
P. 4682. Tegyük fel, hogy egy lift gyorsulása felfelé induláskor ugyanakkora, mint lassulása akkor, amikor megáll valamelyik emeleten. Mekkora ez az érték, ha induláskor az utas súlya az érkezési súlyának \(\displaystyle k\)-szorosa?
Közli: Tornyos Tivadar Eörs, Budapest
(3 pont)
P. 4683. A szertárban elég sok egyforma, \(\displaystyle 100~\Omega\) ellenállású fogyasztónk van. Kettőt sorba kapcsolunk egy 120 V-os áramforrásra. Hány fogyasztót kapcsoljunk az egyikkel párhuzamosan, hogy a másik teljesítménye elérje a 100 W-ot?
Közli: Szombathy Miklós, Eger
(3 pont)
P. 4684. A homorú tükör görbületi középpontjából kiindulva egy pont mozog egyenletesen és egyenes vonalban a tükör optikai középpontjáig. Adjuk meg és ábrázoljuk a kép helyét az idő függvényében!
Strasser V. Benő (1884-1966) feladata
(4 pont)
P. 4685. Az ábrán látható \(\displaystyle M=4m\) tömegű test szabadon csúszhat a vízszintes asztalon. Görbe kiképzésű lapjának jobb oldali része vízszintes. A \(\displaystyle M\) tömegű testre egy \(\displaystyle m\) tömegű, kisméretű testet helyezünk az asztallaptól számított \(\displaystyle H\) magasságban, majd a rendszert magára hagyjuk. A \(\displaystyle m\) tömegű test asztalba ütközésekor a testek \(\displaystyle d=0{,}6\) m távolságra lesznek egymástól. A súrlódás mindenhol elhanyagolható, \(\displaystyle h=0{,}2\) m.
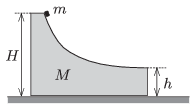
\(\displaystyle a)\) Milyen sebességgel mozognak a testek abban a pillanatban, amikor a \(\displaystyle m\) tömegű test lerepül a \(\displaystyle M\) tömegű testről?
\(\displaystyle b)\) Mekkora sebességgel csapódik a lerepülő test az asztalba?
\(\displaystyle c)\) Határozzuk meg a \(\displaystyle H\) magasságot!
Közli: Kotek László, Pécs
(4 pont)
P. 4686. Vízszintes, légpárnás asztalon két egyforma, \(\displaystyle m\) tömegű, \(\displaystyle R\) sugarú korong egymással érintkezve, a középpontjaikat összekötő irányra merőlegesen, azonos \(\displaystyle v\) sebességgel mozog. A középpontjaikat összekötő szakasz felezőmerőlegesén helyezkedik el egy harmadik, \(\displaystyle M\) tömegű, \(\displaystyle R\) sugarú nyugvó korong középpontja. A mozgó korongok tökéletesen rugalmasan ütköznek a nyugvóval. Ütközés közben a korongok pereme közt sincs súrlódás.
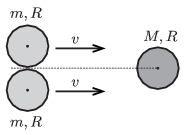
\(\displaystyle a)\) \(\displaystyle M=m\) esetén mekkora lesz az ütközés után a korongok sebességének nagysága és milyen az iránya?
\(\displaystyle b)\) Mekkora \(\displaystyle M/m\) tömegarány esetén mozognak a \(\displaystyle m\) tömegű korongok eredeti sebességük irányára merőlegesen?
Közli: Zsigri Ferenc, Budapest
(5 pont)
P. 4687. A világűrben két pontszerűnek tekinthető test bizonyos távolságra helyezkedik el. Ha az egyik testet nem engedjük elmozdulni, a másik test \(\displaystyle T_1=6\) perc múlva fog nekiütközni. Fordított esetben ez az idő \(\displaystyle T_2=8\) perc. Mennyi idő telik el az ütközésig, ha mindkét test szabadon elmozdulhat?
Közli: Szász Krisztián, Budapest
(5 pont)
P. 4688. Egy hőszigetelt tartályt két részre oszt egy elhanyagolható térfogatú válaszfal. Az egyik rész térfogata 2 dm\(\displaystyle {}^3\), a másiké 3 dm\(\displaystyle {}^3\). A 2 dm\(\displaystyle {}^3\)-es részben 300 K hőmérsékletű, \(\displaystyle 2\cdot 10^5\) Pa nyomású héliumgáz van. A másik térrészben 200 K hőmérsékletű, \(\displaystyle 10^5\) Pa nyomású oxigéngáz van. A válaszfalat eltávolítjuk. Mekkora lesz a keletkező gázkeverék hőmérséklete és nyomása?
Szegedi Ervin (1957-2006) feladata
(4 pont)
P. 4689. Egy termodinamikai hőerőgépben a munkavégző közeg kétatomos molekulájú ideális gáz, mely ciklusonként két izobár és két izochor folyamatból álló egyensúlyi körfolyamaton megy át. A gáz legmagasabb hőmérséklete ebben a körfolyamatban 500 K. Abban a két állapotban, amikor a gáz izochor folyamatról izobárra tér át, egyenlő a hőmérséklet.
Mekkora a gáz legalacsonyabb hőmérséklete a körfolyamat során, ha a gép legnagyobb hatásfoka a két szélső hőmérséklet között zajló körfolyamatban 9,9-szer akkora lehetne, mint amekkora a termodinamikai hatásfok a fenti esetben?
Közli: Radnai Gyula, Budapest
(5 pont)
P. 4690. Két jó szigetelésű kondenzátort feltöltünk kísérletezés céljából. Ha sorba kapcsoljuk őket ellenkező előjelű pólusuk egyesítésével, akkor összesen 166 V-ot, ha pedig párhuzamosan kapcsoljuk őket azonos előjelű pólusaik egyesítésével, akkor 74,4 V feszültséget mérhetünk rajtuk. Az utóbbi esetben az energiaveszteség a kisebb feszültségre töltött \(\displaystyle 10~\mu \rm F\)-os kondenzátor eredeti energiájával egyenlő.
\(\displaystyle a)\) Mekkora feszültségekre töltöttük fel egyenként a két kondenzátort?
\(\displaystyle b)\) Mekkora a másik kondenzátor kapacitása?
Közli: Légrádi Imre, Sopron
(5 pont)
P. 4691. A 400 kW villamos csúcsteljesítményre képes újszilvási napelempark teljes beruházási költsége 618 millió forint volt, és az első teljes év során 685 MWh villamosenergiát termelt. A 2000 MW villamos csúcsteljesítményű Paksi Atomerőmű 2013-ban 15,37 TWh villamosenergiát termelt.
\(\displaystyle a)\) Mivel magyarázható, hogy a villamos csúcsteljesítmények aránya nem azonos az éves villamosenergia-termelések arányával?
\(\displaystyle b)\) Hány forint beruházási költséget igényelne, ha a jelenlegi Paksi Atomerőművet napelemparkkal váltanánk ki?
Közli: Vass Miklós, Budapest
(4 pont)
P. 4692. Vízszintes, homogén, \(\displaystyle B=0{,}05\) T indukciójú mágneses mezőben egy \(\displaystyle L=20\) cm hosszú, \(\displaystyle A=12~\rm cm^2\) keresztmetszetű, \(\displaystyle N=400\) menetszámú, egyenes tekercs vízszintes síkban foroghat a közepén átmenő függőleges tengely körül. A tekercs tengelye kezdetben merőleges a mágneses indukcióvonalakra, és két végén egy-egy \(\displaystyle D=24\) N/m direkciós erejű, \(\displaystyle \ell_0=20\) cm hosszúságú, nyújtatlan, másik végén rögzített csavarrugóhoz csatlakozik az ábra szerint. A rugók kezdetben merőlegesek az egyenes tekercs tengelyére.
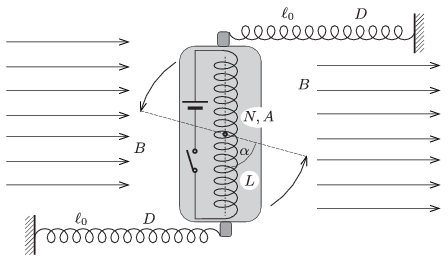
A kapcsoló zárása után a tekercsben áram fog folyni. Mekkora erősségű ez az áram, ha a tekercs \(\displaystyle \alpha=60^\circ\)-os szöggel elfordulva kerül ismét egyensúlyba?
Közli: Holics László, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

