A KöMaL 2015. áprilisi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2015. május 11-én LEJÁRT. |
M. 350. Határozzuk meg egy hagyományos, gáztöltésű izzólámpa burájában lévő gáz nyomását!
Közli: Szeder László, Sárospatak
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2015. május 11-én LEJÁRT. |
P. 4725. A szabványos pingponglabda átmérője 40 mm, tömege 2,7 gramm. Mekkora átmérőjű vasgolyót kellene a pingponglabdához ragasztani, hogy együtt éppen lebegjenek a vízben?
Közli: Vass Miklós, Budapest
(3 pont)
P. 4726. Egy fekete korongot, amelyre vékony, fehér körcikket festettünk, a korong közepén átmenő, rá merőleges tengely körül forgatunk, és stroboszkóppal (periodikusan felvillanó fényforrással) világítunk meg. Milyen összefüggés van a korong \(\displaystyle n\) fordulatszáma és az \(\displaystyle f\) villogási frekvencia között, ha nemcsak egyetlen egy, hanem \(\displaystyle p\) számú, állni látszó fehér körcikket figyelhetünk meg (\(\displaystyle p=2,3,4,\ldots\))?
Orosz feladat
(4 pont)
P. 4727. Egy homogén fémlemezből különböző alakú, de ugyanakkora területű síkidomokat vágunk ki. Milyen alakú síkidomnak lesz a síkjára merőleges és a tömegközéppontján átmenő tengelyre vonatkoztatott tehetetlenségi nyomatéka a lehető legkisebb? (Lásd még a P. 4708. feladat megoldását lapunk 246. oldalán!)
Strasser V. Benő (1884-1966) feladata nyomán
(4 pont)
P. 4728. A Rosetta űrszonda leszálló egysége, a Philae, egy olyan üstökös magjára szállt le, amelynek tömege \(\displaystyle 10^{13}\) kg, és mivel üreges belül, átlagos sűrűsége csak 0,4 g/cm\(\displaystyle {}^3\). A leszállás ,,pattogósra'' sikerült, az első visszapattanás után 113 perc múlva érkezett vissza a Philae az üstökös felszínére. Adjunk becslést a következőkre:
\(\displaystyle a)\) Mekkora az üstökös magjának felszínén a gravitációs térerősség, és mekkora a szökési sebesség?
\(\displaystyle b)\) Legalább mekkora lehetett az első visszapattanás sebessége, és legfeljebb milyen magasra pattanhatott fel a Philae?
A becsléshez az üstökös magját nem forgó, homogén gömbnek tekinthetjük, a mozgást pedig állandó gyorsulású mozgásnak. Az alkalmazott átlagos gyorsulás meghatározásához használjuk fel a visszapattanás sebessége és magassága közötti egzakt összefüggést.
Közli: Radnai Gyula, Budapest
(5 pont)
P. 4729. Függőlegesen álló, \(\displaystyle A=5~{\rm dm}^2\) belső keresztmetszetű hőszigetelt hengerben egy fonálra függesztett, \(\displaystyle M=80~\)kg tömegű, könnyen mozgó dugattyú zár el \(\displaystyle T_0=300~\)K hőmérsékletű levegőt. A dugattyút egy \(\displaystyle D=6~\)N/cm rugóállandójú, nyújtatlan rugó kapcsolja a mennyezethez. A légoszlop hossza \(\displaystyle \ell_0=1{,}2~\)m, kezdetben a külső és a belső nyomás \(\displaystyle p_0=10^5~\)Pa. A fonál egy adott pillanatban elszakad.
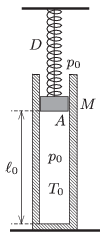
\(\displaystyle a)\) Mekkora lesz a dugattyú legnagyobb sebessége a létrejövő folyamat során?
\(\displaystyle b)\) Mekkora lesz a bezárt levegő legmagasabb hőmérséklete a folyamat során?
Közli: Holics László, Budapest
(5 pont)
P. 4730. Az ábra szerinti kapcsolásban az áramforrások kapocsfeszültsége állandó. A \(\displaystyle C\) kapacitású kondenzátor feszültsége \(\displaystyle 1{,}8\,U_0\). Ha az \(\displaystyle U_0\) kapocsfeszültségű áramforrás pólusait felcseréljük, akkor a kondenzátor feszültsége \(\displaystyle 1{,}4\,U_0\)-ra csökken. Mekkora az \(\displaystyle r/R\) és az \(\displaystyle u_0/U_0\) arány?
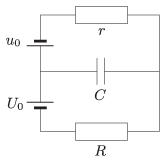
Közli: Zsigri Ferenc, Budapest
(4 pont)
P. 4731. A kriptongázzal töltött volfrámszálas izzólámpa által kisugárzott látható fény egyetlen fotonjának energiája, vagy az izzóban lévő kriptongáz egy atomjának átlagos mozgási energiája nagyobb, amikor be van kapcsolva a lámpa?
Közli: Bigus Imre, Sárospatak
(4 pont)
P. 4732. Egy ciklotronban protonokat, deuteronokat és \(\displaystyle \alpha\)-részecskéket gyorsítanak. A legnagyobb körpálya sugara 50 cm. A mágneses indukcióvektor nagysága 1 tesla. Legfeljebb mekkora energiára gyorsíthatók fel ezek a részecskék a ciklotronban?
Román feladat
(4 pont)
P. 4733. Egy hengeres üvegrúdban a tengelyével párhuzamosan fénysugarak haladnak, majd a rúd végén kilépnek a levegőbe, és egyetlen pontba fókuszálódnak. Adjuk meg a határfelület alakját jellemző görbe egyenletét az üveg \(\displaystyle n\) törésmutatója és az \(\displaystyle f\) fókusztávolság függvényében! (Lásd még a P. 4646. feladat megoldását lapunk 2014. évi októberi számában!)
R. P. Feynman nyomán
(4 pont)
P. 4734. Szigetelő anyagú, vízszintes, sima felületen három darab \(\displaystyle m\) tömegű, kisméretű, pozitív töltésű golyót \(\displaystyle L\) hosszúságú, elhanyagolható tömegű, szigetelő fonalakkal kötöttünk össze. Két golyó töltése \(\displaystyle Q\), a harmadiké pedig \(\displaystyle 2Q\). Egy adott pillanatban a \(\displaystyle Q\) töltésű golyókat összekötő fonalat elvágjuk.
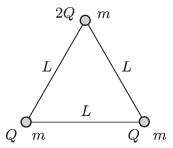
\(\displaystyle a)\) Mekkora lesz a golyók sebessége abban a pillanatban, amikor a \(\displaystyle 2Q\) töltésű golyó sebessége a legnagyobb?
\(\displaystyle b)\) Mekkora erő feszíti a fonalakat ebben a helyzetben?
\(\displaystyle c)\) Mekkora az egyes golyók elmozdulása ebben a pillanatban?
Közli: Kotek László, Pécs
(5 pont)
P. 4735. A Kozmikus Baleseteket Kivizsgáló Intézet (KOBALKIVI) a következő rövid jelentést írta egyik fizikus szakértőjének:
,,A titánfaló kis zöld emberkék egyik kutató űrhajója rátalált egy tökéletesen gömb alakú, homogén, titán anyagú kisbolygóra. A bányászat előkészítésére egy egyenes, a kisbolygó sugarával megegyező hosszúságú alagutat fúrtak, és abba síneket fektettek. (Az alagút mindkét vége a kisbolygó felszínénél volt.) Sajnos az egyik csille, jóllehet befékezték, az alagút egyik végénél belecsúszott az aknába. Eleinte gyorsult, utána fokozatosan lelassult és visszafordult, majd éppen az alagút közepén megállt. A fordulópontnál hajszál híján elütötte az ott álló bányamestert.''
A KOBALKIVI a következő kérdésekre várt választ a szakértőtől:
\(\displaystyle a)\) Hol (az alagút hányad részénél) állt a bányamester?
\(\displaystyle b)\) Mekkora lehetett a csille kerekei és a sínek közötti csúszó súrlódási együttható?
\(\displaystyle c)\) Mennyi ideig mozgott a csille, ha a kisbolygó körül, a felszínhez közel keringő űrszonda keringési ideje 24 óra? (A kisbolygónak nincs légköre.)
Közli: Gnädig Péter, Vácduka
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

