A KöMaL 2016. februári fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2016. március 10-én LEJÁRT. |
M. 357. Vizsgáljuk meg egy lejtőn vízszintes helyzetből elengedett hatszögletű ceruza mozgását! Mérjük meg az állandósult átlagsebességet a lejtő hajlásszögének függvényében!
Varga István (1952-2007) feladata
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2016. március 10-én LEJÁRT. |
P. 4805. 15 m magasan lévő erkélyről felhúzunk egy 40 kg tömegű, 30 m hosszú láncot, amelynek egyik vége már az erkélyen van. A lánc egyik fele függőlegesen lóg, a másik fele a talaj szintjén egy alacsony kupacban fekszik. Mennyi munkát végzünk a lánc felhúzásakor?
(3 pont)
P. 4806. Függőlegesen feldobtunk egy kis követ, amelyet 1,6 másodperc múlva kaptunk el újra. Határozzuk meg, hogy a kezünktől számítva milyen magasra emelkedett a kő, és mekkora volt a kezdősebessége!
(3 pont)
P. 4807. Hány molekula van 1 liter vízben, ha a víz hőmérséklete
\(\displaystyle a)~0~{}^\circ \rm{C};\,\,\,\, b)~ 100~{}^\circ \rm{C}?\)
(3 pont)
P. 4808. Laci és Zoli labdáznak. Először függőlegesen felfelé hajítják a kezükben lévő kisméretű labdát, és azt tapasztalják, hogy minél nagyobb kezdősebességgel indítják el, annál magasabbra emelkedik.
Ezután bizonyos távolságra eltávolodnak egymástól, és így dobják egymás kezébe a labdát. Zoli azt mondja, hogy ebben az esetben is akkor repül magasabbra a labda, ha nagyobb a kezdősebesség. Laci kételkedik ebben, szerinte ez nincs mindig így.
Kinek van igaza?
Közli: Árokszállási Tibor, Paks
(4 pont)
P. 4809. Az indiántábor lakói azonos nyílvesszőket lőnek egy vastag deszkába. Eszes Medve megállapítja, hogy a piros színű nyíl kétszer olyan mélyen hatol be a deszkába, mint a kék színű. Feltételezi, hogy a deszka által a nyílvesszőre kifejtett fékezőerő arányos a pillanatnyi behatolás mélységével. Ezek után több kérdésre is választ tud adni.
\(\displaystyle a)\) Hányszor volt nagyobb a piros nyílvessző becsapódási sebessége, mint a kék színűé?
\(\displaystyle b)\) A piros vagy a kék színű nyílvessző fékezési ideje a nagyobb?
Közli: Simon Péter, Pécs
(4 pont)
P. 4810. Egy 1 kg tömegű testet egy rugóval és egy fonállal az ábrán látható módon függesztünk fel két fal közé. A rugó és a fonál \(\displaystyle 30^\circ\)-os szöget zár be a vízszintessel.
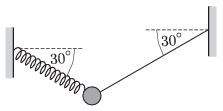
\(\displaystyle a)\) Mekkora erőt fejt ki a rugó?
\(\displaystyle b)\) Mekkora gyorsulással és milyen irányban indul el a test, ha a fonál elszakad?
Nagy László fizikaverseny, Kazincbarcika
(4 pont)
P. 4811. \(\displaystyle A=10~{\rm cm}^2\) keresztmetszetű hengerben \(\displaystyle m=2~{\rm kg}\) tömegű dugattyú \(\displaystyle \ell= 30~{\rm cm}\) hosszú levegőoszlopot zár el. A külső és a belső nyomás egyaránt \(\displaystyle p_0=10^5\) Pa. A cső függőleges tengely körül foroghat. Álló helyzetben a dugattyú közepe a tengelytől \(\displaystyle r= 0{,}5\) m távolságra van.
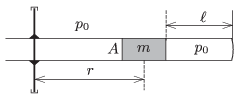
\(\displaystyle a)\) Hányszorosára változik a bezárt gáz sűrűsége, ha a csövet \(\displaystyle \omega=3~{\rm s}^{-1}\) szögsebességgel forgatjuk?
\(\displaystyle b)\) Forgás közben mekkorára kellene lecsökkennie a külső nyomásnak ahhoz, hogy a dugattyú az eredeti helyzetébe kerüljön vissza?
A hőmérséklet mindvégig állandó.
Szegedi Ervin (1956-2006) feladata
(4 pont)
P. 4812. Egy gyűjtőlencse optikai tengelyén a lencsétől \(\displaystyle d\) távolságra egy \(\displaystyle T\) pontszerű fényforrás van. A lencse túlsó oldalán, az optikai tengelyre merőlegesen, a lencsével szemben egy síktükör van.
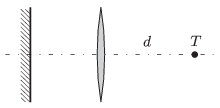
\(\displaystyle a)\) Ha a síktükröt az optikai tengely mentén mozgatjuk, akkor az optikai rendszer által a fényforrásról alkotott kép folyamatosan egybeesik a fényforrással. Hogyan lehetséges ez?
\(\displaystyle b)\) A fényforrás lencsétől mért távolságát megkétszerezzük. Hová helyezzük a síktükröt, hogy a rendszert elhagyó fénysugarak párhuzamosak legyenek egymással?
Közli: Zsigri Ferenc, Budapest
(4 pont)
P. 4813. Tekintsük az ábrán látható hídkapcsolást!
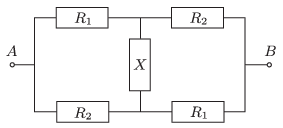
\(\displaystyle a)\) Mekkora a középső ellenállás értéke, ha az \(\displaystyle A\) és \(\displaystyle B\) pontok közötti eredő ellenállás éppen a középső ellenállás nagyságával egyezik meg: \(\displaystyle R_{AB}=X\)?
\(\displaystyle b)\) Megválasztható-e \(\displaystyle X\) értéke úgy, hogy az eredő ellenállás \(\displaystyle R_1\) és \(\displaystyle R_2\) négyzetes közepe legyen: \(\displaystyle R_{AB}=\sqrt{\dfrac{R_1^2+R_2^2}{2}}\)?
(Lásd még ,,A hídkapcsolás eredő ellenállása és áramerősségei'' című cikket Lapunk 105. oldalán, illetve ,,A Milne-egyenlőtlenség és társai, avagy ellenállások álruhában I.'' című cikket a KöMaL 2015. évi decemberi számának 514. oldalán.)
Közli: Bertalan Zoltán, Békéscsaba
(4 pont)
P. 4814. Egy \(\displaystyle M\) tömegű fémgyűrűt \(\displaystyle Q\) pozitív töltéssel töltöttünk fel egyenletesen. A gyűrű az üres térben nyugszik, semmilyen külső erő nem hat rá. Tengelye mentén igen messziről egy \(\displaystyle m\) tömegű, \(\displaystyle q\) pozitív töltésű részecskét indítunk el a gyűrű irányában akkora \(\displaystyle v_0\) sebességgel, hogy éppen át tudjon haladni a gyűrű közepén.
\(\displaystyle a)\) Legalább mekkora a részecske sebessége az egész mozgás folyamán?
\(\displaystyle b)\) Legfeljebb mekkora a gyűrű sebessége ezen esemény során?
\(\displaystyle c)\) Mennyi lesz a részecskének és a gyűrűnek a sebessége a folyamat végén, amikor már messze vannak egymástól?
(Hanyagoljuk el a folyamat során fellépő sugárzási energiaveszteségeket!)
Közli: Lambodar Mishra, Ahmedabah, India
(4 pont)
P. 4815. Miért más a hangfalak ,,iránykarakterisztikája'' magas és a mély hangokra? Ennek alapján magyarázzuk meg, hogy miért erősödnek fel jobban a mély hangok, ha a hangfalakat közvetlenül a fal elé állítjuk!
Közli: Vladár Károly, Kiskunhalas
(5 pont)
P. 4816. Vízszintes síkon rögzített (végtelen hosszúnak tekinthető) vastag, egyenes vezetékben \(\displaystyle I=25\) A erősségű áram folyik. A vezeték mellett, attól \(\displaystyle r_0=1\) cm távolságban \(\displaystyle a=5\) cm, \(\displaystyle b=10\) cm oldalú, téglalap alakú, zárt, rézdrótból készített keret nyugszik a síkon. Az áramot igen rövid idő alatt egyenletesen nullára csökkentjük. Mekkora sebességre tenne szert a keret, ha nem hatna rá súrlódási erő?
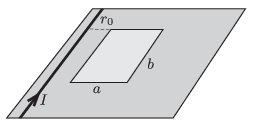
Közli: Holics László, Budapest
(5 pont)
P. 4817. Egy kutya gazdája a partra merőlegesen 5 méterre bedob egy labdát a folyóba. A víz sebessége 0,3 m/s, a kutya a vízhez képest 0,5 m/s sebességgel tud úszni.
\(\displaystyle a)\) Hol és mennyi idő múlva éri utol a kutya a labdát, ha a labda vízbe érkezésekor a vízbe veti magát, és állandóan a labda felé úszik?
\(\displaystyle b)\) Miután a kutya elérte a labdát, azonnal a gazda felé indul, és egyenes vonalú, egyenletes mozgással kiúszik a partra úgy, hogy a parthoz képesti sebessége mindig a gazda felé mutat. A labda elérése után mennyi idővel adja vissza a labdát a kutya a gazdinak?
\(\displaystyle c)\) A gazdi az előzővel megegyező módon újra bedobja a labdát a vízbe. A kutya ugyanúgy utoléri, de ezután görbe vonalú mozgással úgy úszik, hogy a vízhez képesti sebessége mindig a gazdája felé mutat. A labda elérése után mennyi idővel adja vissza a labdát a kutya a gazdinak? (Útmutatás: Érdemes összehasonlítani a kutya és a gazda közötti távolság változásának sebességét a kutya sebességének vízfolyás irányú komponensével.)
Melyik esetben jut vissza a labda hamarabb a gazdihoz, és mekkora ez az időkülönbség?
Nagy László (1931-1987) feladata nyomán
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

