A KöMaL 2016. márciusi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2016. április 11-én LEJÁRT. |
M. 358. Mérjük meg otthoni eszközökkel a ,,vitálkapacitásunkat'' (a teljes belégzésből a teljes kilégzésig eltávozó levegő normál nyomású térfogatát)!
Közli: Vass Miklós, Budapest
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2016. április 11-én LEJÁRT. |
P. 4818. Jancsi és Juliska 250 m-re lakik egymástól. Reggel fél 8-kor egyszerre lépnek ki a házuk kapuján. Juliska 1,1 m/s sebességgel gyalogol az iskola felé. Jancsi - mivel messzebb lakik - 1,5 m/s sebességgel siet. Jancsi éppen az iskola kapujában éri utol Juliskát. Milyen messze van az iskola Juliska lakásától? Hány órakor léptek be a kapun?
(3 pont)
P. 4819. Fél liter vizet forralunk 500 W-os merülőforralóval. Mennyi idő alatt melegszik fel forráspontig a 0,5 liter, \(\displaystyle 20~{}^\circ\)C hőmérsékletű víz, ha a melegítés hatásfoka 80%? Mi lehet az oka a 20%-os energiaveszteségnek, ha a merülőforraló által leadott energia teljes egészében a vízbe kerül?
(3 pont)
P. 4820. Egy ismert fajlagos ellenállású fémhuzal hosszát 0,1%, vastagságát 2% pontossággal tudjuk megmérni. Milyen pontossággal tudjuk kiszámítani a mért adatokból
\(\displaystyle a)\) a huzal térfogatát;
\(\displaystyle b)\) a huzal elektromos ellenállását?
(3 pont)
P. 4821. Egy rugó 10 cm-rel nyúlik meg, ha a rugóra egy \(\displaystyle 400~\mathrm{kg/m}^3\) sűrűségű, tömör parafagömböt függesztünk.
\(\displaystyle a)\) A gömböt a rugóval együtt egy, vizet tartalmazó edénybe helyezzük úgy, hogy a rugó felső vége a gömbhöz, alsó vége az edény aljához van erősítve. Ekkor egyensúlyi helyzetben a gömb fele merül a vízbe, és a rugó feszített állapotban van. Mennyi ekkor a rugó megnyúlása?
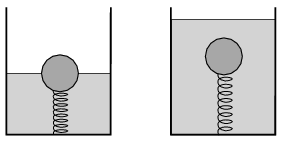
\(\displaystyle b)\) Mennyi lesz a rugó megnyúlása akkor, ha az edénybe annyi vizet töltünk, hogy a parafagömb teljesen a víz alá kerüljön?
Közli: Légrádi Imre, Sopron
(4 pont)
P. 4822. Mekkora szöget kell bezárnia két erőnek, hogy az eredőjük nagysága akkora legyen, mint a két erő nagyságának
\(\displaystyle a)\) négyzetes közepe,
\(\displaystyle b)\) harmonikus közepe?
Mi a feltétele annak, hogy ezek a szögek minimálisak legyenek, és mekkorák a minimális értékek?
Közli: Zsigri Ferenc (Budapest)
(4 pont)
P. 4823. Rögzített, \(\displaystyle \alpha\) hajlásszögű lejtőn két (homogén tömegeloszlású) gömb az ábrán látható módon helyezkedik el. Feltéve, hogy a legördülő gömbök középpontját összekötő egyenes végig függőleges marad, mekkora lehet az \(\displaystyle \alpha\) szög? Mekkora a testek gyorsulása ekkor?
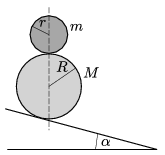
(A tapadó súrlódás elég nagy, és a közegellenállás elhanyagolható.)
Közli: Iván Balázs (Fonyód, Mátyás Király Gimnázium)
(5 pont)
P. 4824. A tó vize a téli hidegben egyre hidegebb lesz. Végül befagy, és a jég is egyre vastagodik. Feltéve, hogy a levegő \(\displaystyle -20~{}^\circ\)C-os, ábrázoljuk vázlatosan, hogyan alakul a hőmérséklet egy adott pillanatban a jég felszínétől kezdve lefelé, egészen a tófenékig.
Közli: Hilbert Margit, Szeged
(4 pont)
P. 4825. Hőszigetelő tartályt hőszigetelő dugattyú oszt egy \(\displaystyle V\) és egy \(\displaystyle 2V\) térfogatú részre. Kezdetben mindkét részben \(\displaystyle T_0=300\) K hőmérsékletű, \(\displaystyle p_0=10^5\) Pa nyomású levegő van. A \(\displaystyle V=2\) liter térfogatú részbe épített \(\displaystyle R=100~\Omega\) ellenállású hődrótos, \(\displaystyle U=230\) V-os melegítőt addig működtetjük, amíg a gázok ,,térfogatot cserélnek'', vagyis az ábra szerinti bal oldali gáz térfogata \(\displaystyle V\)-re, a jobb oldali \(\displaystyle 2V\)-re változik.
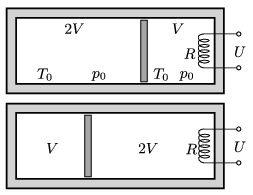
\(\displaystyle a)\) Mekkora lett a hőmérséklet a két tartályban?
\(\displaystyle b)\) Mennyi ideig tartott a folyamat?
Közli: Holics László, Budapest
(5 pont)
P. 4826. Síkkondenzátor párhuzamos lemezeinek \(\displaystyle Q_1={2\cdot10^{-5}}\) C, illetve \(\displaystyle Q_2=5\cdot10^{-5}\) C töltést adtunk, majd a lemezek közé, azokkal párhuzamosan, a lemezek területével megegyező alapterületű töltetlen fémhasábot toltunk. Mekkora töltés található a fémhasáb bal és jobb oldali felületén?
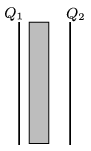
Közli: Kotek László, Pécs
(4 pont)
P. 4827. Határozzuk meg az ábrán látható áramkörben a főágban és a mellékágakban folyó áramerősségek értékét!
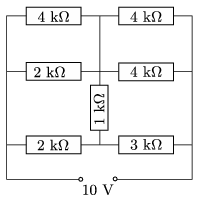
Közli: Simon Péter, Pécs
(4 pont)
P. 4828. Az ábrán látható, \(\displaystyle r\) sugarú szigetelőkorong vízszintes talajon állandó \(\displaystyle v\) sebességgel csúszásmentesen gördül a síkjára merőleges, \(\displaystyle B\) indukciójú, homogén mágneses térben. Középpontját a peremével egy vékony, \(\displaystyle r\) hosszúságú rézrúd köti össze. Ábrázoljuk a rézrúd végei között indukálódó feszültséget a rúdnak a vízszintessel bezárt \(\displaystyle \alpha\) szöge függvényében!
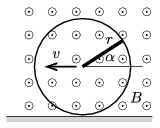
Varga István (1952-2007) feladata
(4 pont)
P. 4829. Két különböző, \(\displaystyle m_1\) és \(\displaystyle m_2\) tömegű csillag egymás gravitációs terében mozog, miközben más erő nem hat rájuk. Egy adott pillanatban a távolságuk \(\displaystyle d_0\), a sebességük pedig olyan és akkora, mintha a közös tömegközéppontjuk körül \(\displaystyle \omega_0\) szögsebességgel keringenének.
\(\displaystyle a)\) Legfeljebb mekkora \(\displaystyle \omega_0\), ha \(\displaystyle d_0\) a két csillag legnagyobb távolsága, és legalább mekkora, ha \(\displaystyle d_0\) a minimális távolságuk?
\(\displaystyle b)\) Mekkora \(\displaystyle \omega_0\) mellett nem képes a gravitáció összetartani a rendszert?
\(\displaystyle c)\) Mekkora a keringési idő, ha a gravitáció együtt tartja a rendszert?
(Lásd még ,,A gravitációs többtestprobléma két speciális esete'' című cikket a KöMaL 2015. évi decemberi számának 558. oldalán.)
Közli: Woynarovich Ferenc, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

