A KöMaL 2016. októberi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2016. november 10-én LEJÁRT. |
I. 409. A Tóték Zrt. különböző méretű, téglatest alakú dobozok készítésével foglalkozik. A dobozok mindegyik oldaléle centiméterben mérve pozitív egész szám. A dobozokat nem lehet szétszedni, de könnyen egymásba pakolhatók, ha a kisebbik doboz megfelelő oldalélei kisebbek a nagyobbik doboz megfelelő oldaléleinél.
Egy futószalagon egymás után helyezkednek el a műhely gyártósoráról érkező dobozok. A cég alkalmazottja az elárusító helyre történő szállítás előtt igyekszik úgy egymásba helyezni a dobozokat, hogy azok minél kevesebb helyet foglaljanak el. Módszere a következő: elindul a futószalag elejétől, és megnézi, hogy a második doboz egymásba helyezhető-e az elsővel. Ha igen, akkor a nagyobbikba beleteszi a kisebbiket, és ezután az így keletkező kétdobozos doboz lesz az első kettő helyén, és most a kezdetben harmadik helyen álló dobozt veti össze az előbb keletkezett dupla dobozzal. Ha ezek is egymásba helyezhetők – akár úgy, hogy az új doboz lesz középen – akkor elvégzi a dobozolást. Ha az első két doboz nem helyezhető egymásba, akkor szintén a harmadik dobozt veti össze az előtte lévővel, ami most a második, és egymásba helyezi őket, ha lehet. Ugyanígy jár el a következő dobozzal, majd a rá következővel, és így tovább az összessel. Vagyis minden esetben egy dobozt próbál összevonni a közvetlenül előtte lévő másik dobozzal vagy dobozcsoporttal.
Segítsünk az alkalmazottnak elvégezni a dobozolást! Készítsünk programot, amely a szalagon lévő dobozok méretei alapján megadja, hogy milyen egymásba helyezés alakítható ki a fenti módszerrel. A standard bemenet első sorában a szalagon érkező dobozok száma található. A bemenet minden további sorában három pozitív egész adja meg az egymás után jövő dobozok három oldalélének nagyságát centiméterben. A standard kimenetre írjuk a dobozolás után kialakított helyzetet: az első sorba a futószalagon most látható dobozok darabszámát, majd az utána következő sorok mindegyikébe írjuk az egyedül álló vagy egymásba ágyazott dobozok eredeti elhelyezkedés szerinti sorszámát. Amennyiben a külső dobozban vannak dobozok, akkor azok sorszáma méret szerint csökkenő sorrendben legyen fölsorolva az adott sorban.
Példaként nézzük meg a következő be- és kimenetet, ahol a tömörség kedvéért a sorvége jelek egy részét / jellel helyettesítettük:
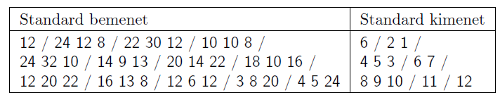
A futószalagon legalább 2, de legföljebb 200 doboz található, melyek mindegyikének mindhárom oldaléle centiméterben mérve 1 és 100 közötti pozitív egész.
Beküldendő egy tömörített i409.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely tartalmazza a megoldás vázlatos leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
I. 410. Ebben a feladatban az európai szuverén államok és az Európai Unióhoz tartozó országok adatait hasonlítjuk össze. Az Európai Unióhoz tartozó országok nevét * karakter egészíti ki. A GDP millió USD-ben van megadva. Néhány ország esetében a GDP-re nincs adat, ezeknél az ,,na'' rövidítés szerepel. (Forrás: hu.wikipedia.org/wiki/Európa_országai, utolsó letöltés: 2016.06.12.)
A feladatok megoldása során ügyeljünk arra, hogy az eredmények helyesek legyenek akkor is, ha új önálló európai országok jönnek létre, illetve ha egyes országok kilépnek az Európai Unióból vagy belépnek abba.
1. Töltsük be a táblázatkezelő program egyik munkalapjára az A1 cellától kezdve az eu.txt adatfájlt, majd mentsük a munkafüzetet europa néven a program alapértelmezett formátumában.
2. Határozzuk meg a D oszlopban függvény segítségével, két tizedes jegyre kerekítve az egyes országok népsűrűségét. Számítsuk ki képlettel az F oszlopban az egyes országok egy főre jutó GDP-jét egész számra kerekítve. Gondoskodjunk arról, hogy ha az adott ország GDP-je nincs megadva, a cella maradjon üresen.
3. Az I1:K6 tartományban statisztikai számításokat kell végeznünk. Az I oszlopban megadott értékeket külön-külön számoljuk ki Európára, illetve az Európai Unióra.
4. Az I8:J11 tartományban egy országot szeretnénk jellemezni. Ehhez a J8-as cellába írjuk be egy európai főváros nevét. Jelenjen meg a J9-es cellában, hogy ez melyik ország fővárosa (a * nélkül). Határozzuk meg, hogy az adott ország egy főre jutó GDP-je hányadik az európai (J10) és az uniós (J11) országok rangsorában.
5. Feltételes formázással
\(\displaystyle a)\) emeljük ki halványkék háttérrel az Unió tagjainak adatait az A:G tartományban,
\(\displaystyle b)\) jelenítsük meg Magyarország adatait piros színű betűvel.
6. Fűzzünk megjegyzést az Egyesült Királyság nevét tartalmazó cellához a következő szöveggel: ,,A 2016. június 23-i népszavazáson a britek többsége az EU-ból való kilépés mellett döntött.''
7. Formázzuk meg a táblázatot az alábbi mintának megfelelően:

Letölthető fájl: eu.txt
Beküldendő egy tömörített i410.zip állományban a megoldást adó táblázatkezelő munkafüzet és egy rövid dokumentáció, amely megadja a felhasznált táblázatkelő nevét és verzióját.
(10 pont)
I. 411. Folyadékok síkbeli modellezésére diffúziós keretmodellt használhatunk. Ennek a lényege: legyen \(\displaystyle T[N,M]\) kétdimenziós táblázat kétféle számmal \(\displaystyle (0,1)\) véletlenszerűen feltöltve. Az 1 a molekulát és a 0 az üres helyet jelenti. A táblázat egy-egy véletlenszerűen kiválasztott molekulájával elemi esemény történhet, amelyet a Szimulációs lépés eljárással adunk meg.
Ha a \(\displaystyle T\) táblázat egy véletlenszerűen kiválasztott molekuláját annak szintén véletlenszerűen kiválasztott szomszédjával megcseréljük, akkor ennek az elemi műveletnek a nagyszámú ismételt végrehajtásával a gázok diffúzióját szimuláljuk. Ezt a modellt bővítjük a molekulák rövidtávú vonzásával, így a síkbeli folyadékmodellhez jutunk.
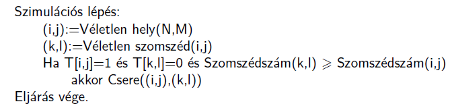
A Véletlen hely() függvény a \(\displaystyle T\) táblázat egy véletlenszerűen kiválasztott cellájának indexeit adja meg. A Véletlen szomszéd() függvény a paraméterként kapott cella véletlenszerű szomszédjának indexeit adja vissza. Lényeges, hogy ne válasszon a táblázaton kívüli helyet. A Csere() eljárás a paraméterként kapott két cella tartalmát cseréli meg.
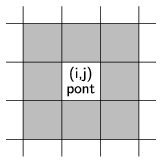
A Szomszédszám() eljárás a paraméterként kapott hely közvetlen szomszédjainak molekulaszámát határozza meg.
Egyszerűbb módszert is készíthetünk a szomszédválasztásra (Véletlen szomszéd()), ha a \(\displaystyle T\) táblázatunkat körülvesszük fallal, 0-kal, amely nem hat a molekulák mozgására. Így a szomszédot a falban is választhatjuk, ha még egy külső falat hozunk létre pl. \(\displaystyle -10\) értékekkel.
Készítsünk programot i411 néven, amely parancssori vagy grafikus felületen a folyadékok síkbeli modelljét bemutatja tetszőlegesen választott \(\displaystyle N\) és \(\displaystyle M\) értékekre.
A programban két beavatkozási lehetőség legyen: Megállítás/Folytatás és Kilépés.
Beküldendő egy tömörített i411.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2016. november 10-én LEJÁRT. |
I/S. 11. Van \(\displaystyle N\) golyónk, ebből \(\displaystyle N-1\) egyforma anyagú, egy golyó pedig különböző. Ránézésre nem tudjuk őket megkülönböztetni, viszont van egy elemző gépünk, ami úgy működik, hogy kiválasztunk \(\displaystyle K\) darab golyót (\(\displaystyle 0< K\le N\)) és a géppel egy elemzés elvégzése után megtudjuk, hogy a különböző golyó a kiválasztott \(\displaystyle K\) darab golyó között van-e. Minden lehetséges \(\displaystyle K\)-ra tudjuk a vizsgálat idejét, vagyis hogy hány percig tart pontosan \(\displaystyle K\) darab golyót megvizsgálni a géppel. Írjunk programot, ami kiszámítja, hogy mi az a legrövidebb időtartam, ami alatt (megfelelő stratégiát követve) meg lehet találni a különböző golyót.
Bemenet: a standard bemenet első sora a golyók \(\displaystyle N\) számát tartalmazza. A második sor \(\displaystyle N\) egész számot tartalmaz, a \(\displaystyle K\)-adik szám (\(\displaystyle L[K]\)) a \(\displaystyle K\) darab golyó megmérésének ideje percben (\(\displaystyle 0< K\le N\)). A mérési idők a golyók darabszáma szerint nemcsökkenő sorozatot alkotnak.
Kimenet: a standard kimenet első és egyetlen sora tartalmazzon egy egész számot, a különböző golyó megtalálásához szükséges legrövidebb időt percben.
Korlátok: \(\displaystyle 1 \le N \le 1000\); \(\displaystyle L[i] \le L[i+1]\) minden \(\displaystyle i\)-re, ahol \(\displaystyle 0< i< N\); \(\displaystyle L[N] \le 10^6\).
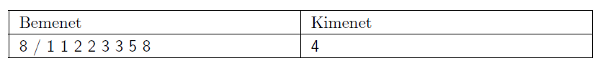
Magyarázat: eredetileg 8 ,,jelöltünk'' van. Megvizsgálunk 4 golyót, ezzel marad 4 jelölt. Ebből megvizsgálunk 2-t, ezután marad 2 jelölt, ezek közül az egyiket megvizsgáljuk. Költség: \(\displaystyle 2+1+1 = 4\).
Pontozás és korlátok: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes 1 mp alatt megoldani a fenti korlátoknak megfelelően.
Beküldendő egy tömörített is11.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2016. november 10-én LEJÁRT. |
S. 110. Peti pénztárcájában \(\displaystyle N\) darab pénzérme van, az \(\displaystyle i\)-ediknek az értéke \(\displaystyle e[i]\). Peti szeretne venni egy gombóc fagyit, de nem emlékszik rá, hogy pontosan mennyibe kerül, csak arra, hogy \(\displaystyle K\) krajcárnál biztosan nem lehet drágább (és az ára krajcárban kifejezve pozitív egész szám). Szeretné tudni, hogy pontosan (visszajáró nélkül) ki tud-e fizetni egy gombóc fagyit, ha csak az első \(\displaystyle R\) darab pénzérmét használja fel, akármennyi is legyen a fagyi ára. Segítsünk Petinek.
A standard bemenet első sora a kérdések \(\displaystyle Q\) számát és a pénzérmék \(\displaystyle N\) számát tartalmazza. A második sor \(\displaystyle N\) egész számot tartalmaz, a pénztárca tartalmát, az \(\displaystyle i\)-edik szám az \(\displaystyle i\)-edik pénzérme \(\displaystyle e[i]\) értéke. Ezután következik a \(\displaystyle Q\) kérdés leírása, minden kérdés külön sorban: a kérdéses \(\displaystyle K\) maximális összeg, és az \(\displaystyle R\) szám.
A standard kimenet \(\displaystyle s\)-edik sora az \(\displaystyle s\)-edik kérdésre adott válasz: ha minden \(\displaystyle K\)-nál nem drágább fagyi pontosan kifizethető az első \(\displaystyle R\) darab érme fölhasználásával, akkor IGEN, egyébként a NEM szó kerüljön a sorba.
Korlátok: \(\displaystyle 1\le Q\le 10^5\), \(\displaystyle 1\le N\le 10^5\), \(\displaystyle 1\le K\le 10^{18}\), \(\displaystyle 1\le R\le N\), \(\displaystyle 1\le e[i]\le 10^9\), időlimit: 1 mp, memórialimit: 256 MB.
Pontozás: Az első 2 tesztesetben \(\displaystyle N\le 1000\) és \(\displaystyle K\le 1000\) (2 pontért);
A következő 3 tesztesetben az összes kérdésben \(\displaystyle R=N\) (további 3 pontért).
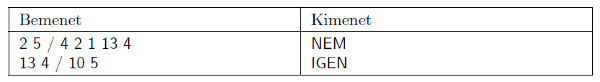
Magyarázat.
Első kérdés: például 12 krajcárt sehogyan sem lehet kifizetni az első négy pénzérmével.
Második kérdés: \(\displaystyle \mathbf{1}=1\), \(\displaystyle \mathbf{2}=2\), \(\displaystyle \mathbf{3}=2+1\), \(\displaystyle \mathbf{4}=4\), \(\displaystyle \mathbf{5}=4+1\), \(\displaystyle \mathbf{6}=4+2\), \(\displaystyle \mathbf{7}=2+1+4\), \(\displaystyle \mathbf{8}=4+4\), \(\displaystyle \mathbf{9}=4+1+4\), \(\displaystyle \mathbf{10}=4+2+4\).
Pontozás és korlátok: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani a fenti korlátoknak megfelelően.
Beküldendő egy tömörített s110.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

