A KöMaL 2016. decemberi informatika feladatai

I-jelű feladatok A beküldési határidő 2017. január 10-én LEJÁRT.

I. 415. Egy \(\displaystyle N\times M\) (\(\displaystyle 1\le N,M\le 40\)) méretű, téglalap alakú területre egy karakter vastag szegélyű téglalapokat raktak egymásra úgy, hogy oldalaik párhuzamosak a terület oldalaival. A téglalapok kitöltetlenek és átfedhetik egymást. A téglalapok száma \(\displaystyle DB\) (\(\displaystyle 0\le DB\le 26\)) és mindegyik keretvonala az angol ábécé egy-egy nagybetűjéből áll. A terület a téglalapok egymás utáni elhelyezése következtében kialakuló betűrendszert mutatja. A terület egyetlen betűvel sem érintett mezőin a ,,.'' karakter szerepel.

Készítsünk programot i415 néven, amely megadja, hogy milyen sorrendben rakták egymásra a téglalapokat. Ha több megoldás is lehetséges, akkor elegendő egyet megadni.

A program olvassa be a standard input első sorából \(\displaystyle N\)-et, \(\displaystyle M\)-et, majd a következő \(\displaystyle M\) sorból soronként \(\displaystyle N\) darab, szóközzel elválasztott karaktert: a területen kialakuló betűrendszert. A program írja a standard outputra a téglalapok lerakásának egy lehetséges sorrendjét.

Beküldendő egy tömörített i415.zip állományban a program forráskódja és rövid dokumentációja, amely tartalmazza a megoldás vázlatos leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

megoldás, statisztika

I. 416. A magyarországi városok néhány adata áll rendelkezésünkre a varos.txt állományban (2013. július 15-i állapot, forrás: https://hu.wikipedia.org/wiki/Magyarország_városai.) A megye.txt a jelenlegi megyéket tartalmazza. Néhány jelenlegi megye korábban több megye egyesítésével jött létre, ezért a korábbi megyenevek a regimegye.txt állományban találhatók. Az állományok tabulátorral tagolt, UTF-8 kódolású szövegfájlok, az első sorok a mezőneveket tartalmazzák.

1. Készítsünk új adatbázist i416 néven. A mellékelt adatállományokat importáljuk az adatbázisba a forrásállományokkal azonos néven.

2. Beolvasáskor állítsuk be a megfelelő adatformátumokat és kulcsokat.

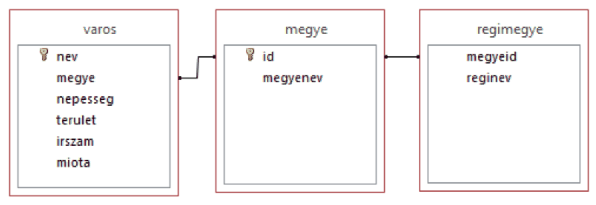
Készítsük el a következő feladatok megoldásait. Az egyes lekérdezéseknél ügyeljünk arra, hogy mindig csak a kért értékek jelenjenek meg és más adatok ne. A megoldásokat a zárójelben lévő néven mentsük el.

3. Határozzuk meg, hogy hány város van megyénként az adatbázisban. Csak a megye neve és a városok száma jelenjen meg, szám szerint csökkenő sorrendben. A listában Budapest ne szerepeljen. (3db)

4. Listázzuk ki a három legsűrűbben lakott város nevét, népességét, területét és népsűrűségét a népsűrűség szerint csökkenő sorrendben. A népsűrűség egész számra kerekítve jelenjen meg. (4suru)

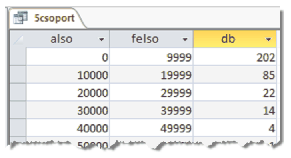
5. Készítsünk lekérdezést az alábbi ábra alapján, amely a városokat népességük alapján 0-tól kezdve \(\displaystyle 10\,000\)-es csoportokba sorolja, és megjeleníti, hogy az egyes csoportokba hány város tartozik. (5csoport)

6. Lekérdezéssel listázzuk ki névsorban a városok nevét és egy mult nevű számított mezőt. A mező tartalma az 1885 előtt városi rangot kapott települések esetén az ,,1885 előtt'' szöveg, az ennél fiatalabb, de 100 évnél régebben várossá nyilvánított települések esetén pedig a ,,több mint 100'' szöveg legyen. A többi város esetén pedig tartalmazza a várossá nyilvánítás évét. (6mult)

7. Gyakori, hogy a város neve tartalmazza annak a megyének a nevét is, ahová (eredetileg) tartozott. Jelenítsük meg, hogy melyek azok a városok, amelyek tartalmazzák a régi megyéjük nevét, és azt is, hogy most melyik megyéhez tartoznak. (7megye)

8. Kérjük be egy város nevét, és listázzuk ki a vele azonos megyében lévő, népességében tőle legfeljebb 10%-kal eltérő városok nevét, népességét. (8konkurrens)

9. Kérjük be egy város nevét, és listázzuk ki azoknak a városoknak nevét, irányítószámát és megyéjét, amelyek más megyében vannak, de irányítószámuk első jegye azonos a választott városéval. (9irszam)

Beküldendő egy tömörített i416.zip állományban az adatbázis, valamint egy rövid dokumentáció, amelyből kiderül az alkalmazott adatbázis-kezelő neve és verziószáma.

Letölthető fájlok: varos.txt, megye.txt, regimegye.txt.

(10 pont)

megoldás, statisztika

I. 417. Fizikai tanulmányainkból ismert, hogy egy rugóra függesztett pontszerű test az egyensúlyi helyzetből való kitérítés és elengedés után harmonikus rezgőmozgást végez: a kitérés az időtől szinuszosan függ. A harmonikus rezgőmozgás előállítható egy körpályán állandó nagyságú sebességgel mozgó pont merőleges vetületeként is.

A harmonikus rezgőmozgás egy egyenes mentén történik. Ha a test mozgását két egymásra merőleges harmonikus erő határozza meg, akkor bonyolultabb síkbeli mozgást kapunk. Ilyenkor a mozgó test pályájának merőleges vetületei harmonikus rezgőmozgások, de a test pályája a két rezgőmozgás összetétele, melynek alakja a két rezgés frekvenciájától és fáziskülönbségétől függ. Ha a frekvenciák hányadosa racionális szám, akkor a test pályája ún. Lissajous-görbe lesz. Az alábbi ábra néhány ilyen görbét mutat be.

Készítsünk a Geogebra program segítségével munkalapot a Lissajous-görbék előállítására. A két egymásra merőleges harmonikus rezgőmozgást két körpályán mozgó pont vetületeként állítsuk elő. A Lissajous-görbét leíró pont a munkalapon úgy mozogjon, hogy annak két merőleges vetülete a kapott két harmonikus rezgőmozgást végző pont legyen.

A két körpályán mozgó test periódusidejének és fáziskülönbségének beállítását csúszkák segítségével tegyük lehetővé.

Beküldendő egy i417.zip tömörített állományban a Geogebra munkalap és dokumentációja, amely tartalmazza a megoldás rövid leírását.

(10 pont)

megoldás, statisztika

I/S-jelű feladatok A beküldési határidő 2017. január 10-én LEJÁRT.

I/S. 13. A rendőrség már hónapok óta figyel egy veszélyes bűnözőt. A megfigyelés során összesen \(\displaystyle N\) fontos helyen bukkant fel, és megfigyelték, hogy ha egy adott helyen van, akkor vagy taxival megy tovább, vagy gyalogol, viszont utóbbi esetben mindig ugyanarra. Tehát ha az \(\displaystyle i\)-edik helyről gyalog megy tovább, akkor mindig egy adott \(\displaystyle B_{i}\) helyen fog legközelebb felbukkanni.

A mai napra elég bizonyíték gyűlt össze ellene, így elhatározták, hogy letartóztatják. A kapcsolatai révén erről biztosan értesült a bűnöző, így semmiképpen sem fog taxival menni, mivel a taxisok feladhatják a rendőrségnek, vagyis gyalog fog menekülni. A rendőrök sajnos nem ismerik a bűnöző mostani helyzetét, viszont elkezdték visszanézni az \(\displaystyle N\) fontos hely biztonsági kameráit. Bíznak benne, hogy hamarosan az egyik kamera felvételein megtalálják. Addig is minket kértek meg, hogy mind az \(\displaystyle N\) helyszínre dolgozzunk ki egy ,,elfogási tervet''. Az elfogási terv az \(\displaystyle i\)-edik helyszín esetén egy olyan \(\displaystyle Q_{i}\) helyre vezényli ki a rendőröket, hogy ha az \(\displaystyle i\)-edik helyen járt a bűnöző és ezután csak gyalog haladt (a kifigyelt mintát követve), akkor akármilyen régi is a felvétel, biztosan fel fog még bukkanni a \(\displaystyle Q_{i}\) helyen. Írjunk programot, ami a megfigyelés eredménye alapján minden helyre megad egy elfogási tervet.

A standard bemenet első sora a helyek \(\displaystyle N\) számát, a következő sor pedig \(\displaystyle N\) egész számot tartalmaz, az \(\displaystyle i\)-edik szám a fent említett \(\displaystyle B_{i}\) érték.

A standard kimenet első és egyetlen sora \(\displaystyle N\) egészet tartalmazzon, az \(\displaystyle i\)-edik szám az \(\displaystyle i\)-edik pontra kidolgozott elfogási tervben szereplő \(\displaystyle Q_{i}\) hely sorszáma legyen. Több megoldás esetén bármelyik megadható.

Korlátok: \(\displaystyle 1\le N\le 10^{6}\), \(\displaystyle 1\le B_{i}\), \(\displaystyle Q_{i}\le N\). Időlimit: 0,1 mp. Memórialimit: 256 MB. A verem (stack) méretére nincs külön korlát, de a teljes memórialimitbe számít bele.

Minta:

Magyarázat: a menekülési útvonalak az alábbiak:

1-es pont: \(\displaystyle 1\to 2\to 2\to 2\to \ldots\)

2-es pont: \(\displaystyle 2\to 2\to 2\to \ldots\)

Pontozás és korlátok: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani a fenti korlátoknak megfelelően.

Beküldendő egy tömörített is13.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

statisztika

S-jelű feladatok A beküldési határidő 2017. január 10-én LEJÁRT.

S. 112. Egy város úthálózata párhuzamos sugárutakból és ezekre merőleges, egymással párhuzamos utcákból áll. A szomszédos utcák távolsága 100 méter, ahogyan a szomszédos sugárutaké is. Az egyszerűség kedvéért az utcákat sorban 1-től \(\displaystyle N\)-ig, míg a sugárutakat szintén sorban 1-től \(\displaystyle M\)-ig megszámozták. A városban nagy problémát jelent, hogy nincs tűzoltóság, így a városvezetés elhatározta, hogy épít egy tűzoltó központot. A központ épületének tervei már el is készültek, így tudjuk, hogy a tűzoltóautók az egyik útkereszteződésnél fognak kihajtani. A városban a tűzoltást tűzcsapok segítik, melyeket \(\displaystyle K\) darab kijelölt kereszteződésbe el is helyeztek. Minden tűzcsapnak tudjuk a helyét, illetve azt, hogy mennyire gyakori az, hogy a közelében tűz üt ki (\(\displaystyle p_{i}\) egész szám a tűz gyakoriságát jelöli az \(\displaystyle i\)-edik kereszteződés közelében). Ha tűz üt ki valahol, akkor a tűzoltóautók állandó sebességgel rögtön elindulnak a megfelelő tűzcsaphoz, csak utcákat és sugárutakat használva, a lehető legrövidebb úton. Úgy szeretnék kiválasztani a központ helyét, hogy a tűzesetekre való kiérkezési idő várható értéke minimális legyen. Ez akkor teljesül, ha \(\displaystyle \sum_1^K p_{i}\cdot d_{i}\) minimális, ahol \(\displaystyle d_{i}\) az \(\displaystyle i\)-edik tűzcsap és a központ távolsága. Készítsünk programot, amely megadja a legkedvezőbb útkereszteződés helyét.

A standard bemenet első sora az utcák \(\displaystyle N\) számát és a sugárutak \(\displaystyle M\) számát, illetve a tűzcsapok \(\displaystyle K\) számát tartalmazza. Az ezután következő \(\displaystyle K\) sor egy-egy tűzcsap pozícióját, illetve a tűz gyakoriságát írja le; minden sor három egész számot tartalmaz: az első az utca, a második a sugárút száma, a harmadik a gyakoriság.

A standard kimenet első és egyetlen sorába a tűzoltóság tervezett helye kerüljön, vagyis két egész szám jelölje a kihajtó helyét: az első az utca, a második a sugárút sorszámát. Több megoldás esetén bármelyik megadható.

Korlátok: \(\displaystyle 1\le N,M\le 10^{9}\), \(\displaystyle 1\le K\le 10^{5}\), \(\displaystyle 1\le p_{i}\le 100\). Időlimit: 0,1 mp. Memórialimit: 256 MB. A verem (stack) méretére nincs külön korlát, de a teljes memórialimitbe számít bele.

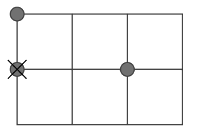
Az ábra a mintát tartalmazza, a körök a tűzcsapok, az \(\displaystyle X\) a tűzoltóság optimális helye.

Pontozás és korlátok: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani a fenti korlátoknak megfelelően.

Beküldendő egy tömörített s112.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

megoldás, statisztika