A KöMaL 2017. februári matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2017. március 10-én LEJÁRT. |
K. 535. El lehet-e helyezni az 1, 2, 3, 4, 5, 6, 7, 8, 9 és 10 számokat az ábrán látható csillagötszögben úgy, hogy minden négy számot tartalmazó egyenes mentén az összeg ugyanannyi legyen?
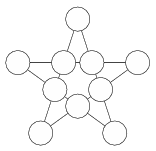
(6 pont)
K. 536. Határozzuk meg az ábrán látható csillagötszög szögeire \(\displaystyle \alpha + \beta + \gamma +\delta + \varepsilon\) értékét.
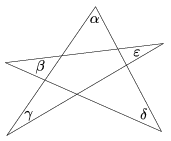
(6 pont)
K. 537. Hány olyan többszöröse van a 9-nek, melynek minden számjegye különböző páros szám?
(6 pont)
K. 538. A 2592 számot ,,nyomtatóbiztos'' számnak nevezzük, mert a \(\displaystyle 2^5\, 9^{2}\) szorzatot rosszul, 2592-nek nyomtatva nem okozunk hibát, hiszen a szorzat eredménye is ennyi. Keressük meg, hogy a 13942125 szám miért nyomtatóbiztos, azaz mely számjegyeket lehetne benne kitevőnek értelmezni, hogy az eredmény a szám maradjon?
(6 pont)
K. 539. Hányféleképpen lehet ráírni egy kocka csúcsaira az 1, 2, 3, 4, 5, 6, 7 és 8 számokat úgy, hogy minden lapon ugyanannyi legyen a lap csúcsaiban álló számok összege? (Két megoldás ugyanannak számít, ha mindkét kockán minden számnak ugyanazok a számok a szomszédai.)
(6 pont)
K. 540. Az XL bolygón egy évben 180 nap, egy hónapban 10 nap van. Minden hetedik évben XL évet tartanak, ami azt jelenti, hogy a harmadik hónap 11 napos. A ,,hét'' 5 napos, napjai sorrendben: AX, EX, IX, OX és UX.
Pax egy XL év negyedik havának első napján született, a mai OX napon éppen 25 éves. Fia, FélX pedig ma 2 éves, 3 hónapos és 5 napos. Amikor FélX éppen feleannyi napos lesz, mint édesapja, nagykorúvá avatják. A ,,hét'' melyik napjára fog esni FélX avatási ünnepsége?
Javasolta: Lorántfy László (Dabas)
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2017. március 10-én LEJÁRT. |
C. 1399. 50 méteres futásban Marci 4 méter előnyt adva Bálintnak, még éppen be tudja érni a célban. Ha Bálint ad 15 méter előnyt Henriknek 200 méteren, épp egyszerre érnek célba. Hány méter előnyt adhat Marci Henriknek 1000 méteren, hogy éppen együtt érjenek célba? (Tegyük fel, hogy mindhárman végig egyenletesen, mindig ugyanazzal a sebességgel futnak.)
(5 pont)
C. 1400. Bizonyítsuk be, hogy ha egy konvex hatszög belső szögei egyenlők, akkor a hatszög bármely két szemközti oldalának különbsége ugyanakkora.
(5 pont)
C. 1401. Az \(\displaystyle x\), \(\displaystyle y\) pozitív számok kielégítik az \(\displaystyle x^3+y^3=x-y\) egyenletet. Igazoljuk, hogy \(\displaystyle x^2+y^2<1\).
(5 pont)
C. 1402. Egy négyzet oldalaira kifelé vele egyező oldalhosszúságú szabályos háromszögeket és négyzeteket rajzoltunk, kettőt-kettőt (minden oldalra egyet). Mekkora annak a lehető legkisebb körnek a sugara, amely teljesen lefed egy ilyen összetett alakzatot?
(5 pont)
C. 1403. Egy \(\displaystyle n\) elemű halmaznak feleannyi \(\displaystyle k-1\) elemű részhalmaza van, mint \(\displaystyle k\) elemű, és \(\displaystyle \frac 74\)-szer annyi \(\displaystyle k + 1\) elemű részhalmaza van, mint \(\displaystyle k\) elemű. Határozzuk meg a halmaz \(\displaystyle k\) elemű részhalmazainak számát.
Javasolta: Koncz Levente (Budapest)
(5 pont)
C. 1404. Az \(\displaystyle ABC\) egyenlő szárú háromszög \(\displaystyle AB\) alapjának \(\displaystyle F\) felezőpontjából a \(\displaystyle BC\) oldalra bocsátott merőleges talppontja \(\displaystyle D\). Az \(\displaystyle FD\) szakasz felezőpontja \(\displaystyle G\). Mutassuk meg, hogy \(\displaystyle AD\) merőleges \(\displaystyle CG\)-re.
(5 pont)
C. 1405. Egy zsákban összesen 10 golyó van, ebből 6 piros. A játék a következő: véletlenszerűen kihúzunk négyet a golyók közül, és ha azok között \(\displaystyle k\) db piros van, akkor \(\displaystyle k^2\) forintot kapunk. Mekkora a nyereségünk várható értéke, ha egy játék 1 forintba kerül?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2017. március 10-én LEJÁRT. |
B. 4849. Az \(\displaystyle ABC\triangle\) beírt körének középpontja \(\displaystyle K\), az \(\displaystyle AB\) oldalhoz hozzáírt kör középpontja \(\displaystyle L\). Mutassuk meg, hogy a körülírt kör \(\displaystyle C\)-vel szemközti \(\displaystyle AB\) íve és a \(\displaystyle KL\) szakasz felezik egymást.
(3 pont)
B. 4850. Oldjuk meg a következő egyenletrendszert a valós számok halmazán:
\(\displaystyle \sqrt{x_1}+\sqrt{x_2}+\ldots+\sqrt{x_{2016}} =\sqrt{2017}\,,\)
\(\displaystyle x_1+x_2+\ldots+x_{2016} =2017.\)
Javasolta: Szoldatics József (Budapest)
(3 pont)
B. 4851. Bizonyítsuk be, hogy ha az
\(\displaystyle x^3-px^2+qx-r=0 \)
egyenlet mindhárom gyöke pozitív, akkor a gyökök reciprok értékeinek összege legfeljebb \(\displaystyle \frac{p^2}{3r}\).
Javasolta: Kovács Márton (Budapest)
(4 pont)
B. 4852. Az \(\displaystyle ABC\) háromszögbe és a háromszög köré az ábra szerint írtuk az \(\displaystyle A_1B_1C_1\) és \(\displaystyle A_2B_2C_2\) háromszögeket, ahol \(\displaystyle A_1B_1\parallel A_2B_2\), \(\displaystyle B_1C_1\parallel B_2C_2\) és \(\displaystyle C_1A_1\parallel C_2A_2\) is teljesül. Az \(\displaystyle ABC\), \(\displaystyle A_1B_1C_1\) és \(\displaystyle A_2B_2C_2\) háromszögek területei rendre \(\displaystyle t\), \(\displaystyle t_1\) és \(\displaystyle t_2\).
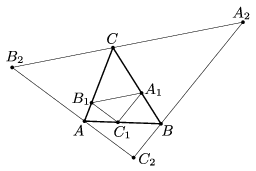
Bizonyítsuk be, hogy \(\displaystyle t^2=t_1\cdot t_2\).
Javasolta: Róka Sándor (Nyíregyháza)
(5 pont)
B. 4853. Legyen az \(\displaystyle ABCD\) érintőnégyszög beírt körének középpontja \(\displaystyle K\). Vegyük fel az \(\displaystyle AK\) szakaszon az \(\displaystyle M\), a \(\displaystyle CK\) szakaszon pedig az \(\displaystyle N\) pontot úgy, hogy \(\displaystyle 2 MBN\sphericalangle= ABC\sphericalangle\) legyen. Bizonyítsuk be, hogy ekkor \(\displaystyle 2 MDN\sphericalangle=ADC\sphericalangle\).
(5 pont)
B. 4854. Legyenek \(\displaystyle a_1,a_2,\dots,a_n\) valós számok. Tekintsük az ezekből képezett \(\displaystyle 2^n-1\) (nemüres) összeget. Hány lehet ezek közül pozitív?
(5 pont)
B. 4855. Egy táblázatot 0 és 1 számokkal töltöttünk ki úgy, hogy nincs két azonos sor, azonban bármelyik két oszlop és négy sor által meghatározott \(\displaystyle 4\times 2\)-es résztáblázatban van két azonos sor. Igazoljuk, hogy van olyan oszlop, amelyben az egyik szám pontosan egyszer fordul elő.
Javasolta: Lelkes Ádám
(6 pont)
B. 4856. A \(\displaystyle \mathcal{H}\) ponthalmaznak a \(\displaystyle P\) pont konvexitási centruma, ha \(\displaystyle \mathcal{H}\cup H_P'\) konvex, ahol \(\displaystyle H_P'\) a \(\displaystyle \mathcal{H}\) ponthalmaz \(\displaystyle P\)-re vonatkozó centrális tükörképe. Mutassuk meg, hogy
\(\displaystyle a)\) minden konvex síknégyszögnek létezik három különböző, nem kollineáris konvexitási centruma;
\(\displaystyle b)\) egy tetraédernek nincs konvexitási centruma.
(6 pont)
B. 4857. Határozzuk meg azokat az \(\displaystyle (n,k)\) pozitív egészekből álló számpárokat, amelyekre \(\displaystyle \big(2^{2^n}+1\big)\big(2^{2^k}+1\big)\) osztható \(\displaystyle nk\)-val.
Bolgár feladat
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2017. március 10-én LEJÁRT. |
A. 689. Legyen \(\displaystyle f_1,f_2,\ldots\) folytonos \(\displaystyle \mathbb{R}\to\mathbb{R}\) függvényeknek egy végtelen sorozata úgy, hogy bármely \(\displaystyle k\) pozitív egészhez és bármely \(\displaystyle r>0\) és \(\displaystyle c\) valós számokhoz létezik olyan \(\displaystyle x\in(-r,r)\) szám, amelyre \(\displaystyle f_k(x)\ne cx\). Mutassuk meg, hogy létezik olyan \(\displaystyle a_1,a_2,\ldots\) valós számsorozat, amelyre \(\displaystyle \sum_{n=1}^\infty a_n\) konvergens, de bármely \(\displaystyle k\) pozitív egész esetén \(\displaystyle \sum_{n=1}^\infty f_k(a_n)\) divergens.
(5 pont)
A. 690. Az \(\displaystyle ABCD\) konvex négyszög \(\displaystyle A\) csúcsából a \(\displaystyle BC\) egyenesre bocsátott merőleges talppontja \(\displaystyle P\), a \(\displaystyle BD\) egyenessel vett metszéspontja \(\displaystyle U\). Az \(\displaystyle A\) pontból a \(\displaystyle CD\) egyenesre bocsátott merőleges talppontja \(\displaystyle Q\), a \(\displaystyle BD\) egyenessel vett metszéspontja \(\displaystyle V\). A \(\displaystyle BU\) szakasz felezőpontja \(\displaystyle S\), a \(\displaystyle DV\) szakasz felezőpontja \(\displaystyle R\). A \(\displaystyle PS\) és \(\displaystyle QR\) egyenesek az \(\displaystyle E\) pontban metszik egymást. A \(\displaystyle PQE\) és \(\displaystyle RSE\) körök második, \(\displaystyle E\)-től különböző metszéspontja \(\displaystyle M\). Az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\), \(\displaystyle E\), \(\displaystyle M\), \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle R\), \(\displaystyle S\), \(\displaystyle U\), \(\displaystyle V\) pontok mind különbözők. Mutassuk meg, hogy a \(\displaystyle BCD\) kör középpontja, az \(\displaystyle AUV\) kör középpontja és az \(\displaystyle M\) pont egy egyenesre esik.
(5 pont)
A. 691. Legyen \(\displaystyle c\ge3\) egész szám, és definiáljuk az \(\displaystyle a_1,a_2,\dots\) sorozatot a következő rekurzióval:
\(\displaystyle a_1=c^2-1, \quad a_{n+1}=a_n^3-3a_n^2+3 \quad (n=1,2,\ldots). \)
Mutassuk meg, hogy bármely \(\displaystyle n\ge2\) egészre az \(\displaystyle a_n\) számnak van olyan prímosztója, amely nem osztja \(\displaystyle a_1,\ldots,a_{n-1}\) egyikét sem.
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

