KöMaL Problems in Physics, May 2017
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on June 12, 2017. |
M. 369. Measure the rotational inertia of a AA battery (Mignon) about its axis of symmetry (\(\displaystyle a\)), and about the axis (\(\displaystyle b\)) which is perpendicular to the previous one and goes through the centre of mass of the battery.
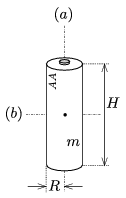
Give the result in terms of \(\displaystyle mR^2\) and \(\displaystyle mH^2\). (\(\displaystyle R\) is the radius of the battery, \(\displaystyle H\) is its height and \(\displaystyle m\) is its mass.)
(6 pont)
 |
Problems with sign 'G'Deadline expired on June 12, 2017. |
G. 602. An initially empty water tank of height 3 meters can be filled with the water of a well in two different ways. Once through tap \(\displaystyle \rm Cs_2\) the water is pumped into the bottom of the tank, and the other is through tap \(\displaystyle \rm Cs_1\) the water is made to flow into the tank from above.
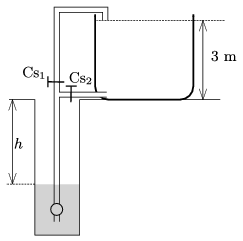
\(\displaystyle a)\) Which one is cheaper?
\(\displaystyle b)\) Somebody calculated that if the losses at the pump and the friction of the flowing water in the tubes are neglected, then the tank can be filled with 20% less energy when the tank is filled in the less energy consuming way. At what depth is the water in the well? (The well is rich in water and the water level in it is constant.)
(3 pont)
solution (in Hungarian), statistics
G. 603. A finely wrought cogwheel is rotated, its teeth cease a thin laser beam travelling through them. The beam is reflected in a mirror at a distance of \(\displaystyle d=1000\) m from the wheel such that it arrives at its starting point through the same gap between the teeth. The speed of the wheel is increasing uniformly and 1 minute after its start it reaches the value of 600 rotations per second. How long does it take after starting the wheel, until the reflected beam on the side of the light source disappears? There are 300 teeth on the wheel, and the size of a tooth is the same as the size of a gap.
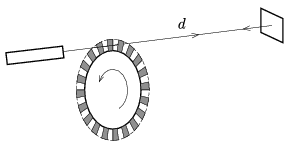
(3 pont)
solution (in Hungarian), statistics
G. 604. There are two small objects on an \(\displaystyle L=3\) m-long wooden board, supported at its middle by a wedge. The masses of the objects are \(\displaystyle m_1=0.2\) kg and \(\displaystyle m_2=0.3\) kg. Between the objects there is a compressed small spring of negligible mass. The spring is compressed to a length of \(\displaystyle \ell=0.3\) m, and tied with a thread. The wedge is exactly below the centre of mass of the system.
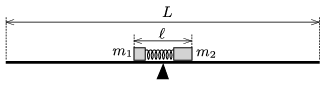
The thread is burnt, and the spring launches the object with mass \(\displaystyle m_1\) at a speed of \(\displaystyle v_1=2\) m/s. To which direction and when will the board be tilted? (Friction is negligible.)
(3 pont)
 |
Problems with sign 'P'Deadline expired on June 12, 2017. |
P. 4938. A crate of mass \(\displaystyle m=10\) kg was pulled along the level ground at a force of magnitude \(\displaystyle F=30\) N. The crate was initially at rest and the force makes an angle of \(\displaystyle \alpha=30^\circ\) with the horizontal. How much distance did the crate cover and what was its final speed if 120 J work was done? (The coefficient of kinetic friction is \(\displaystyle \mu=0.2\).)
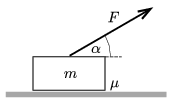
(4 pont)
solution (in Hungarian), statistics
P. 4939. A ball was projected at point \(\displaystyle A\) and it hit a wall at point \(\displaystyle B\) horizontally. From \(\displaystyle B\) the ball ``flies'' to the points \(\displaystyle C_1, C_2, \dots,\) and finally gets back to point \(\displaystyle A\). The coefficient of restitution is \(\displaystyle \varepsilon\) at any point. Find \(\displaystyle \varepsilon\), if the ball does not bounce up at all when it gets back to point \(\displaystyle A\).
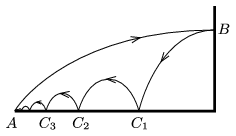
(It can be assumed that the air-drag exerted on the ball is negligible and the ball does not start rotating.)
(5 pont)
solution (in Hungarian), statistics
P. 4940. An object of mass \(\displaystyle m=0.8\) kg is attached to one end of a spring of spring constant \(\displaystyle D=30\) N/m. The other end of the spring is attached to the top of a fixed slope of angle of elevation of \(\displaystyle \alpha=30^\circ\). The coefficients of static and kinetic friction between the object and the slope are both \(\displaystyle \mu=0.23\). The object is released at the unstretched position of the spring.
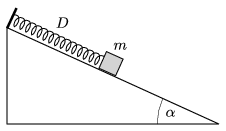
\(\displaystyle a)\) What is the greatest speed of the object?
\(\displaystyle b)\) What is the greatest extension of the spring?
\(\displaystyle c)\) Where will the object eventually come to rest?
(5 pont)
solution (in Hungarian), statistics
P. 4941. In a big water reservoir the height of the water is \(\displaystyle H\). Next to the reservoir there are \(\displaystyle N\) number of cylinder shaped water tanks (each at the level of the bottom of the reservoir). The tanks are connected with alike thin tubes. The water tank at one end of the tank system is connected to the bottom of the reservoir through a thicker tube, whilst at the other end of the tank system there is an – initially closed – tap.
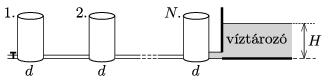
If the tap is opened, then after a long enough time the total volume of the water in the tanks decreases by a value of \(\displaystyle V_0\). What is the diameter of the tanks? (The flow of the water is viscous.)
(4 pont)
solution (in Hungarian), statistics
P. 4942. A sphere of diameter 1 m is made of some good thermally insulating material, and a spherical electric stove of diameter 20 cm is put into it. The stove releases heat into all directions uniformly at a rate of 10 W. To what temperature will surface of the stove be heated if the the outer surface of the thermally insulating material is \(\displaystyle 20~{}^\circ\)C, and its thermal conductivity is \(\displaystyle 0.04~\rm W/(m\cdot K)\)?
(5 pont)
solution (in Hungarian), statistics
P. 4943. At the centre of a cylinder-shaped glass there is an opaque metal cylinder. There is some transparent liquid in the glass around the cylinder. Observing the cylinder from a distant point, due to the refraction of light the part of the cylinder in the liquid seems wider. At what extent?
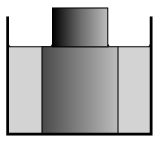
Data: the radius of the glass is 4 cm, the radius of the metal cylinder is 2.5 cm and the refractive index of the liquid is 1.5.
(5 pont)
solution (in Hungarian), statistics
P. 4944. The charge of a parallel plate condenser is \(\displaystyle Q\), the distance between its plates is \(\displaystyle d\). The condenser is placed into uniform electric field of magnitude \(\displaystyle E_0\), the direction of the electric field is perpendicular to the plates. How much work is done if the condenser is turned by 180 degree about an axis which is perpendicular to the external electric field? (In other words the plates of the condenser are swapped.)
(4 pont)
solution (in Hungarian), statistics
P. 4945. During the decay of a free stationary neutron three particles are born: a proton, an electron and an anti-neutrino. The energy of the electron can be any value within a certain range (the energy spectrum is continuous). It may occur that during a decay an electron of negligibly small kinetic energy is produced. What is the speed of the arousing proton in this case? (The rest mass of anti-neutrino can be considered zero.)
(5 pont)
solution (in Hungarian), statistics
P. 4946. A trolley of mass \(\displaystyle m\) can move freely in a box of mass \(\displaystyle m\). The box can move on the tabletop which is covered by a thin layer of oil, the frictional force depends on only the speed of the box: \(\displaystyle \boldsymbol F=-k\boldsymbol v\). Initially the box stays at rest, and the trolley starts from the wall on the left-hand side at a speed of \(\displaystyle v_0\) and moves towards the wall on the right. How many times will the trolley of length \(\displaystyle \ell\) collide elastically with the box of length \(\displaystyle L\)? (The elastic collision is ensured by the small springs attached to the trolley, their length is much smaller than \(\displaystyle \ell\).)
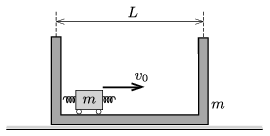
(5 pont)
solution (in Hungarian), statistics
P. 4947. In a particle accelerator stationary particles of mass \(\displaystyle M\) are hit by objects of different masses and different speeds. (The speed is comparable to the speed of light.) The collisions are straight, head on and totally elastic.
\(\displaystyle a)\) Determine the energy \(\displaystyle W\) given to an initially stationary particle as a function of the kinetic energy \(\displaystyle E_{\rm m}\) and the linear momentum \(\displaystyle I\) of the moving particle.
\(\displaystyle b)\) Sketch the \(\displaystyle W(E_{\rm m}, I)\) function at fixed \(\displaystyle I=I_0\) linear momentum and at fixed \(\displaystyle E_{\rm m}=E_0\) kinetic energy.
\(\displaystyle c)\) Investigate the non-relativistic and the ultra relativistic limiting cases.
(5 pont)
solution (in Hungarian), statistics
P. 4948. Two cylinder-shaped rods made of the same material and having the same cross section collide such that they move along their common symmetry axis. The lengths of the rods are \(\displaystyle \ell_1\) and \(\displaystyle \ell_2\), whilst their speeds are \(\displaystyle v_1\) and \(\displaystyle v_2\), and the collision is straight and head on. The rods are elastic and for the deformations and stresses that occur in them at any point and at any time Hooke's law holds true. What is the coefficient of restitution in this collision?
(6 pont)
Upload your solutions above.
