A KöMaL 2017. októberi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2017. november 10-én LEJÁRT. |
I. 436. (É) Ha egy szabályos dobókockát feldobunk, leesés után ugyanakkora valószínűséggel lesz a kocka tetején az első hat pozitív egész szám valamelyikének megfelelő számú pont. Erre a továbbiakban arab számjegyekkel hivatkozunk: 1, 2, 3, 4, 5, 6.
Ebben a feladatban szabályos dobókockával történő dobást szimulálunk, illetve az így kapott sorozatot elemezzük. Készítsünk programot dobokocka néven a következő feladatok megoldására.
1. Kérjünk be a felhasználótól egy tippet, majd szimuláljunk egy kockadobást szabályos dobókockával. Írassuk ki a képernyőre a felhasználó tippjét és a dobás eredményét is, majd tájékoztassuk a felhasználót az eredményről a következő formában: ,,Ön eltalálta.'' vagy ,,Ön nem találta el.''. (Az ékezetmentes kiírás is elfogadott.)
2. Szimuláljunk egy \(\displaystyle N (\le 10\,000)\) dobásból álló kísérleti dobássorozatot, és az eredményt tároljuk el egy megfelelő típusú változóban. Az \(\displaystyle N\) értékét a felhasználótól kérjük be. Írassuk ki a dobássorozatot (elválasztójelek nélkül) a kiserlet.txt szöveges állomány első sorába is, ezt egy szóközzel elválasztva kövesse \(\displaystyle N\) értéke. A továbbiakban az így kapott sorozatot elemezzük.
3. Számoljuk meg, hogy a kísérlet során hányszor dobtuk az egyes számokat. Írassuk ki relatív gyakoriságukat két tizedesjegy pontossággal a kiserlet.txt fájl második sorába, egy-egy szóközzel elválasztva (pl. 1-16,51% 2-17,23% ...).
4. Hányszor fordult elő a kísérlet során, hogy egymás után pontosan két hatost dobtunk? Az eredményt írassuk a kiserlet.txt fájl harmadik sorába.
5. Hányszor fordult elő a kísérlet során, hogy a kocka két egymást követő dobás esetén két egymással szemben lévő oldalára esett? (Közismert, hogy a szabályos dobókocka szemben lévő oldalain szereplő számok összege 7.) A választ írassuk a kiserlet.txt fájl 4. sorába. (Például a 21612 sorozat kettőnek számít.)
6. Előfordult-e a kísérlet során, hogy hat egymást követő dobás során mind a hat lehetséges értékre sor került? Írassuk a választ (Igen vagy Nem) a kiserlet.txt fájl 5. sorába. Ha a válasz Igen, adjuk meg egy ilyen sorozat kezdetének a helyét is az Igen után egy szóközzel elválasztva. (A minta tagjainak számozását eggyel kezdjük.)
7. Előfordult-e a kísérlet során legalább \(\displaystyle M\) tagú palindrom? (Olyan részsorozat, amely elölről hátulra és hátulról előre olvasva megegyezik, például: 2345432.) Az \(\displaystyle M\) értékét kérjük be a felhasználótól. Írjuk a választ és \(\displaystyle M\) értékét egy szóközzel elválasztva a kiserlet.txt fájl 6. sorába (például: Nem 12). Ha a válasz Igen, adjuk meg egy ilyen sorozat kezdetének a helyét is egy szóközzel elválasztva.
8. Milyen hosszú volt a leghosszabb, azonos számjegyekből álló sorozat? Írassuk ki a választ a kiserlet.txt fájl 7. sorába, továbbá egy szóközzel elválasztva írassuk mellé egy ilyen részsorozat első tagjának helyét is.
Beküldendő egy i436.zip tömörített állományban a program forráskódja és dokumentációja, amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
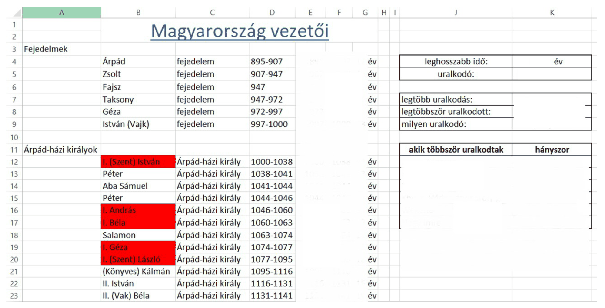
I. 437. Magyarország fejedelmeit, királyait, uralkodóit, államfőit és miniszterelnökeit sorolja fel a MEK kisokos (forrás: http://mek.niif.hu/00000/00056/html/240.htm, utolsó letöltés: 2017-09-20). A feladat ezen adatok feldolgozása lesz táblázatkezelő program segítségével. A táblázat tartalmazza, melyik házból való uralkodóról van szó, vagy fejedelemről, államfőről, esetleg miniszterelnökről, a nevet, az uralkodóházat vagy egyéb megnevezést és hogy mettől meddig tartotta fenn a tisztséget. Vannak olyan személyek, akik megszakításokkal, de többször voltak hivatalban, ők többször szerepelnek a listában. A táblázatban szereplő utolsó államfő Göncz Árpád, utolsó miniszterelnök pedig Horn Gyula, egészítsük ki a táblázatot napjainkig.
1. Töltsük be a magyarvezetok.txt szövegfájlt a táblázatkezelő egy munkalapjára az A1-es cellától kezdődően. Munkánkat i437 néven mentsük el a táblázatkezelő alapértelmezett formátumában.
2. Az E oszlop celláiban írassuk ki, mikor kezdte meg az uralkodását, mikor lépett hivatalba az adott személy. Másolható képletet használjunk és ügyeljünk arra, hogy vannak üres sorok a táblázatban.
3. Az F oszlop celláiba írassuk ki, meddig uralkodott, volt hivatalban az éppen aktuális ciklusában az adott személy.
4. A G oszlopban számítsuk ki, hány évig volt hivatalban az adott személy összesen élete során.
5. A minta alapján számítsuk ki a K oszlop adott celláit! K4-ben adjuk meg, hány évig volt vezető a leghosszabb időt ott töltő személy, a K5-ben pedig, hogy ki volt az.
6. A K7-es cellában adjuk meg ki volt, aki legtöbbször töltött be vezetői tisztséget, a K8-ba ki volt ez, a K9-be pedig, hogy milyen hivatalt töltött be. Ha több azonos is van, elég az elsőt kiírni.
7. A I12-es cellától lefelé gyűjtsük ki azokat a királyokat, vezetőket, akik többször voltak hivatalban, mellé, hogy összesen hányszor.
8. Feltételes formázással a B oszlopban azoknak az uralkodóknak a nevét piros háttérszínnel emeljük ki, akiknek a keresztneve először szerepel az ország történetében. Például: I. Béla.
9. Hasonlítsuk össze diagram segítségével a Habsburg-ház és a Habsburg– Lotaringiai-ház uralkodóinak trónon töltött évei számát, amelyből kiderül, mely ház uralkodói töltöttek több évet összesen a trónon.
10. Az első sorban lévő ,,Magyarország vezetői'' cím link legyen, és a http://mek.niif.hu/00000/00056/html/240.htm oldalra mutasson.
Beküldendő egy tömörített i437.zip állományban a megoldást adó táblázatkezelő munkafüzet és egy rövid dokumentáció, amely megadja a felhasznált táblázatkelő nevét és verzióját.
Letölthető állomány: magyarvezetok.txt
(10 pont)
I. 438. Készítsünk táblázatkezelő alkalmazásban táblázatot vagy írjunk programot, amely egy kavicsot terítő robot munkáját vezérli.
A robot egy \(\displaystyle 10\times 10\) cellás négyzetrácson mozoghat a szövegesen megadott utasítások szerint. A robot mozgása a lehető legegyszerűbb, mert egyszerre előre, hátra, illetve jobbra vagy balra (E, H, J és B) egy egységet tud lépni. Amikor a robot új cellába lép, köveket vesz fel, ha a kövek száma az adott cellában 1-nél több, és köveket tesz le, ha van nála kő, a cellában pedig éppen nincs. A robot a bal felső sarok cellájából indul, felfelé néz és nincs nála kavics. Működése során először lép és utána változtathatja a cellában a kavicsok számát. A vezérlés utasításainak száma legfeljebb 100.
A \(\displaystyle 10\times 10\) cellás négyzetrács celláinak kavicsszáma és a robotot vezérlő utasítássor áll rendelkezésre a terep.txt állományban. Vagy töltsük be a táblázatkezelőbe az A1-es cellától kezdődően, vagy a program standard bemenetén adjuk meg a szóközökkel tagolt terep.txt állományt. A megoldás során a forrásadatok módosulása esetén is helyes eredményt kell kapnunk.
A táblázatkezelő az L1-es cellában, vagy a program a standard kimeneten jelenítse meg, hogy a vezérlés befejezése után hány kő van a robotnál.

Beküldendő egy tömörített i438.zip állományban a táblázatkezelő munkafüzet, vagy a program forráskódja és rövid dokumentációja, amely megadja a táblázatkezelő alkalmazás nevét és verziószámát, illetve azt, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
A megoldáshoz szükséges letölthető állomány: terep.txt
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2017. november 10-én LEJÁRT. |
I/S. 20. Egy elektromos terepjáró autóval szeretnénk eljutni egy dimbes-dombos területen az egyik helyről a másikra. A területet gondolatban \(\displaystyle N \times M\) egyforma négyzetre osztjuk, és minden egyes négyzethez egy magassági adatot rendelünk. A négyzetek számozása a bal felső saroktól indul jobbra, illetve lefelé. Az autó útját úgy modellezzük, mintha egy-egy oldalukkal egymással érintkező négyzeteken haladna keresztül. Az egyik négyzetről a másikra történő mozgáskor az autó 1 egységnyit meríti az akkumulátorát, ha a két négyzet azonos magasságban van. Alacsonyabb magasságban lévő négyzetről magasabban lévő négyzetre mozgáskor a szintkülönbség kétszerese plusz 1 egységnyit merül az akkumulátor. Amikor az autó lefelé halad, akkor a szintkülönbség számértékének megfelelő egységnyit töltődik az akkumulátor, miközben 1 egységet merül. Az autó indulási pontja a térkép \(\displaystyle (s_i, s_j)\) négyzete, a cél a térkép \(\displaystyle (c_i, c_j)\) négyzete.
Kérdés, hogy legkevesebb hány egységnyi töltéssel kell rendelkeznie az autónak a kiindulási négyzetben, hogy eljusson a cél négyzetbe úgy, hogy közben egyszer sem kell külső energiával tölteni, csupán a szintkülönbség csökkenésekor kap energiát. Az autó nem tud továbbmenni, ha egy négyzetbe érve nem pozitív az energiája, ezért az csak a cél négyzetben lehet 0.
A feladatot megoldó program olvassa be a standard bemenetről a térképhez tartozó \(\displaystyle N\) és \(\displaystyle M\) értékét, majd a következő \(\displaystyle N\) sor mindegyikében \(\displaystyle M\) pozitív egész \(\displaystyle h_{i,j}\) számot, melyek a térkép \(\displaystyle i\)-edik sorában és \(\displaystyle j\)-edik oszlopában lévő négyzet szintértékét adják, illetve a következő sorban az induló és cél négyzetek adatait: \(\displaystyle s_i\), \(\displaystyle s_j\), \(\displaystyle c_i\), \(\displaystyle c_j\). A program írja a szabványos kimenetre a legkisebb akkumulátor töltöttséget, amellyel az autó a kiindulási helyről a célba érhet.
Példa:
| Bemenet | Kimenet |
4 5 1 2 4 3 4 1 1 3 5 2 1 3 2 3 4 1 2 1 1 3 3 2 1 4 | 7 |
Korlátok: \(\displaystyle 1 \le N, M \le 100\), \(\displaystyle 1 \le h_{i,j} \le 1000\).
Értékelés: a megoldás lényegét leíró dokumentáció 1 pontot ér. További 9 pont kapható arra a programra, amely a korlátoknak megfelelő bemenetekre helyes kimenetet ad 1 másodperc futásidő alatt. Részpontszám kapható arra a programra, amely csak kisebb \(\displaystyle N\) és \(\displaystyle M\) értékek esetén ad helyes eredményt 1 másodpercen belül.
Beküldendő egy is20.zip tömörített állományban a megoldást leíró dokumentáció és a program forráskódja.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2017. november 10-én LEJÁRT. |
S. 119. Ifjú hercegünk egy hegyi ösvényen készül átkelni. Az ösvény mentén manók állnak lesben, akikkel semmiképp nem jó találkozni. Szerencsére a manók mindegyike olyan, hogy egy bizonyos színt nem lát. Hercegünk ezért varratott magának mindegyik színből egy-egy köpenyt, így ha a megfelelő manó előtt elhaladva azt viseli, akkor a manó nem veszi észre. A köpenyek mindegyike karra terítve is könnyen vihető, és emellett tetszőleges számú köpeny – akár az összes – egymásra fölvéve hordható. Ha a herceg már visel egy vagy több köpenyt, akkor a következőt azok fölé tudja venni. Vetkőzéskor mindig a legfelső köpenyt tudja levenni, tehát ha szüksége van egy most nem legfelül viselt köpenyre, akkor az összes fölötte lévőt le kell vennie.
A herceg azt is megtudta, hogy milyen sorrendben következnek az egyes manók az ösvény mentén. Mivel nem szeretne sokszor öltözni, ezért szeretné tudni, hogy hogyan juthat túl a lehető legkevesebb számú öltözéssel az ösvényen. Az út megkezdése előtt nem viseli egyik köpenyt sem, és az ösvény után sem, tehát leveszi, ami még rajta van. Minden köpeny föl- vagy levétele egy öltözésnek számít.
A feladatot megoldó program olvassa be a standard bemenetről a manók \(\displaystyle N\) számát, illetve az általuk nem látott színek \(\displaystyle Z\) számát, majd a következő sorból \(\displaystyle N\) számú pozitív egészet: az \(\displaystyle i\)-edik szám az \(\displaystyle i\)-edik manó által nem látott szín \(\displaystyle m_i\) sorszáma. A program írja a standard kimenetre az ösvényen való áthaladáshoz szükséges legkevesebb öltözések számát.
Példák:
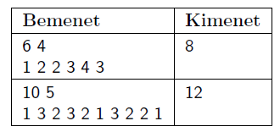
Korlátok: \(\displaystyle 1 \le Z \le N \le 30\), \(\displaystyle 1 \le m_i \le Z\).
Értékelés: a megoldás lényegét leíró dokumentáció 1 pontot ér. További 9 pont kapható arra a programra, amely a korlátoknak megfelelő bemenetekre helyes kimenetet ad 1 másodperc futásidő alatt. Részpontszám kapható arra a programra, amely csak kisebb \(\displaystyle N\) értékek esetén ad helyes eredményt 1 másodpercen belül.
Beküldendő egy s119.zip tömörített állományban a megoldást leíró dokumentáció és a program forráskódja.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

