KöMaL Problems in Mathematics, October 2017
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on November 10, 2017. |
K. 553. A bag contains the numbers 1 to 200, written on cards. Andrew and Bill take turns drawing number cards one by one until the bag is empty. At the end, each of them adds his numbers together. Given that the first number drawn by Andrew is 3 and Bill's first number is 170, by what maximum amount may Andrew's sum exceed Bill's sum at the end?
(6 pont)
solution (in Hungarian), statistics
K. 554. The integers 1 to 2017 are listed as follows: first those numbers not divisible by 3 are written down in increasing order. Then the list continues with those numbers that are divisible by 3 but not divisible by 9, followed by those divisible by 9 but not divisible by 27, and so on.
\(\displaystyle a)\) What is the last number of the list?
\(\displaystyle b)\) In which position will 2017 be in the list?
\(\displaystyle c)\) In which position will 2016 be in the list?
(6 pont)
solution (in Hungarian), statistics
K. 555. For which three consecutive integers is their product five times their sum?
(6 pont)
solution (in Hungarian), statistics
K. 556. In a lattice of unit squares, is there a pentagon whose vertices are all lattice points and whose sides are all \(\displaystyle \sqrt 5\) units long?
(6 pont)
solution (in Hungarian), statistics
K. 557. The midpoints of the sides of a square \(\displaystyle ABCD\) are \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle R\) and \(\displaystyle S\). They are connected to the vertices of the square as shown in the figure. Prove that \(\displaystyle AT = TV\).
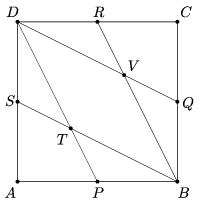
(6 pont)
solution (in Hungarian), statistics
K. 558. For which positive integers \(\displaystyle n\) will \(\displaystyle n^{4}+n^{2}+1\) be a prime?
(6 pont)
 |
Problems with sign 'C'Deadline expired on December 11, 2017. |
C. 1434. In a running race organized in Munich, the participants started simultaneously and ran along a set path. 30 minutes after the start of the race, a car set out from the starting line and followed the runners at uniform speed. For each participant, the race terminated whenever the car caught up with him or her. The female winner was overtaken by the car at 68 km, and the male winner was overtaken at 92 km, 1 hour and 36 minutes later. Assuming that they also ran at uniform speed, what were the speeds of the two winners, and what was the speed of the car?
(5 pont)
solution (in Hungarian), statistics
C. 1435. Inside a square of side 2 units, semicircles are drawn over two adjacent sides as diameters. What is the radius of the circle that touches one semicircle and the side of the square internally, and touches the other semicircle externally?
Proposed by D. Fülöp, Pécs
(5 pont)
solution (in Hungarian), statistics
C. 1436. We have eight red cubes and eight white cubes, all congruent. We select eight cubes and form a large cube out of them. How many differently coloured large cubes may we obtain? Two cubes are differently coloured if they cannot be rotated into each other.
Matlap, Kolozsvár
(5 pont)
solution (in Hungarian), statistics
C. 1437. Problem C. 1437. was incorrectly stated in our October issue. Solutions for the corrected problem will be accepted together with those in the November issue.
Given that each of nine distinct lines divides the area of a square in a \(\displaystyle 2:3\) ratio in such a way that none of the lines cuts a triangle off the square. Prove that there are three concurrent lines among them.
(5 pont)
solution (in Hungarian), statistics
C. 1438. Prove that the equation \(\displaystyle x^2+y^3=z^4\) has no solution of prime numbers \(\displaystyle x\), \(\displaystyle y\), \(\displaystyle z\).
(5 pont)
solution (in Hungarian), statistics
C. 1439. For what value of \(\displaystyle c\) will the simultaneous equations
\(\displaystyle {(x-5)}^2+ {(y-1)}^2 =c,\)
\(\displaystyle {(x-1)}^2+ {(y-5)}^2 =c\)
have a unique solution?
(5 pont)
solution (in Hungarian), statistics
C. 1440. In the unit cube \(\displaystyle ABCDA'B'C'D'\), let \(\displaystyle M\) and \(\displaystyle N\) denote the perpendicular projections of points \(\displaystyle D'\) and \(\displaystyle B\) onto the diagonal \(\displaystyle B'D\) of the cube, respectively. Determine the area of quadrilateral \(\displaystyle BND'M\).
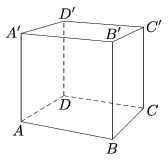
Matlap, Kolozsvár
(5 pont)
 |
Problems with sign 'B'Deadline expired on November 10, 2017. |
B. 4894. Seven thieves have stolen some golden coins, and now each of them takes a share of the loot in the following manner. They proceed in alphabetical order of their names, and everyone takes as many coins as the sum of the digits of the number of coins in the heap not distributed yet. The last coin is removed when two full circles are completed. It turns out that everyone has received the same number of coins, only the chief got more. What was the position of the chief in the alphabetical order?
Matlap, Kolozsvár
(4 pont)
solution (in Hungarian), statistics
B. 4895. Prove that if \(\displaystyle n-1\) and \(\displaystyle n+1\) are both primes and \(\displaystyle n> 6\) is an integer then \(\displaystyle n^2(n^2+16)\) is divisible by 720.
English competition problem
(3 pont)
solution (in Hungarian), statistics
B. 4896. Let \(\displaystyle A_1\), \(\displaystyle B_1\), \(\displaystyle C_1\), \(\displaystyle D_1\) denote the midpoints of the sides of a convex quadrilateral \(\displaystyle ABCD\). Let \(\displaystyle A_2\), \(\displaystyle B_2\), \(\displaystyle C_2\), \(\displaystyle D_2\) denote the midpoints of the sides of the quadrilateral \(\displaystyle A_1B_1C_1D_1\). The procedure is continued. Prove that if quadrilateral \(\displaystyle A_1B_1C_1D_1\) is cyclic then quadrilateral \(\displaystyle A_{2017}B_{2017}C_{2017}D_{2017}\) is also cyclic.
Proposed by J. Szoldatics, Budapest
(3 pont)
solution (in Hungarian), statistics
B. 4897. Given \(\displaystyle n\) points in the plane, show that it is possible to select three, denoted by \(\displaystyle A\), \(\displaystyle B\) and \(\displaystyle C\), such that \(\displaystyle \angle ABC\le 180^\circ /n\).
(4 pont)
solution (in Hungarian), statistics
B. 4898. Let \(\displaystyle A\) be a four-element set of positive integers such that \(\displaystyle ab+13\) is a perfect square for all \(\displaystyle a,b\in A\), \(\displaystyle a\ne b\). Prove that each element of \(\displaystyle A\) leaves a remainder of 2 when divided by 4.
Proposed by G. Nyul, Debrecen
(4 pont)
solution (in Hungarian), statistics
B. 4899. The degree of each vertex of a simple planar graph \(\displaystyle G\) is 3, and \(\displaystyle G\) can be drawn in the plane with its edges represented by non-intersecting unit line segments. Show that \(\displaystyle G\) has at least \(\displaystyle 8\) vertices.
(5 pont)
solution (in Hungarian), statistics
B. 4900. Let \(\displaystyle K\) be a convex shape symmetric in the origin, let \(\displaystyle e\) be a line through the origin, and let \(\displaystyle e'\) be any line parallel to \(\displaystyle e\). Let, furthermore \(\displaystyle \# H\) denote the number of lattice points in a set \(\displaystyle H\). Prove that \(\displaystyle \# (K\cap e)+1 \ge \# (K\cap e')\).
(5 pont)
solution (in Hungarian), statistics
B. 4901. An epidemic broke out in Smurf village after a few residents contracted a disease. Luckily, every smurf recovers from the illness in one day, and then they will be immune to the disease for another day. However, from the following day onwards they may catch the disease again. The transition between the sick and healthy states always occurs at night when the smurfs are sleeping. Unfortunately, the smurfs never give up their habit of visiting all their friends every day, not even when they are ill. So when a sick smurf meets a healthy but not immune one, the latter will inevitably catch the disease. Given that Smurf village has 100 inhabitants, show that the epidemic will necessarily terminate by the 101th day following the outbreak.
Collected at the Budapest Univ. Technology and Economics
(6 pont)
solution (in Hungarian), statistics
B. 4902. Let \(\displaystyle A_1B_1\), \(\displaystyle A_2B_2\), \(\displaystyle A_3B_3\) and \(\displaystyle A_4B_4\) be four parallel line segments of different lengths given in the plane. For any \(\displaystyle 1\le i<j\le 4\), let \(\displaystyle M_{ij}\) denote the intersection of lines \(\displaystyle A_iB_j\) and \(\displaystyle A_jB_i\). Show that the lines \(\displaystyle M_{12}M_{34}\), \(\displaystyle M_{13}M_{24}\) and \(\displaystyle M_{14}M_{23}\) are either concurrent or parallel.
(6 pont)
 |
Problems with sign 'A'Deadline expired on November 10, 2017. |
A. 704. A regular triangle has side length \(\displaystyle n\). We divided its sides into \(\displaystyle n\) equal parts and drew a line segment parallel with each side through the dividing points. A lattice of \(\displaystyle 1+2+\cdots+(n+1)\) intersection points is thus formed. For which positive integers \(\displaystyle n\) can this lattice be partitioned into triplets of points which are the vertices of a regular triangle of side length \(\displaystyle 1\)?
Proposed by Alexander Gunning, Cambridge, UK
(5 pont)
A. 705. Triangle \(\displaystyle ABC\) has orthocenter \(\displaystyle H\). Let \(\displaystyle D\) be a point distinct from the vertices on the circumcircle of \(\displaystyle ABC\). Suppose that circle \(\displaystyle BHD\) meets \(\displaystyle AB\) at \(\displaystyle P\ne B\), and circle \(\displaystyle CHD\) meets \(\displaystyle AC\) at \(\displaystyle Q\ne C\). Prove that as \(\displaystyle D\) moves on the circumcircle, the reflection of \(\displaystyle D\) across line \(\displaystyle PQ\) also moves on a fixed circle.
Proposed by Michael Ren, Andover, Massachusetts, USA
(5 pont)
A. 706. Let \(\displaystyle \mathbb{Z}^+\) denote the set of positive integers. Find all functions \(\displaystyle f\colon \mathbb{Z}^+\to\mathbb{Z}^+\) which satisfy the following:
\(\displaystyle \bullet\) \(\displaystyle f(mn)=f(m)f(n)\) for all \(\displaystyle m,n\in\mathbb{Z}^+\), and
\(\displaystyle \bullet\) \(\displaystyle f^{(n)}(n)=n\) for all \(\displaystyle n\in\mathbb{Z}^+\) (in other words, \(\displaystyle f\Big(f\big(\dots \big(f(n)\big)\dots\big)\!\Big)=n\), where there are \(\displaystyle n\) pairs of brackets on the left-hand side).
Korean problem
(5 pont)
Upload your solutions above.
