A KöMaL 2017. novemberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2017. december 11-én LEJÁRT. |
M. 372. Készítsünk egy hengeres műanyag (PET) palackból homokórát. A palack kupakján alakítsunk ki egy (kb. 8-10 mm átmérőjű) lyukat, és azon keresztül pergessük ki a palackból a száraz homokot. Mérjük meg, hogyan függ az időegységenként kiáramló homok mennyisége a palackbeli homokszint magasságától!
Közli: Gnädig Péter, Vácduka
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2017. december 11-én LEJÁRT. |
G. 613. Körpályán mozgó jármű állandó, 72 km/h nagyságú sebességgel halad. Mennyi időnként kerül ugyanabba a pontba, ha gyorsulásának nagysága 1,6 m/s\(\displaystyle ^2\)?
(3 pont)
G. 614. Egy \(\displaystyle D\) direkciós állandójú, elhanyagolható tömegű rugó végeihez azonos, \(\displaystyle m\) tömegű korongokat erősítettünk. A rugót és a korongokat a rugó nyújtatlan állapotában egy légpárnás asztalra helyezzük, és a rugó tengelyének irányában \(\displaystyle v_0\) sebességű mozgásba hozzuk. Egy adott pillanatban a hátul lévő korongot hirtelen megállítjuk, és fogva tartjuk.
\(\displaystyle a)\) Mennyi idő múlva fordul vissza a másik test?
\(\displaystyle b)\) Mekkora lesz a rugó legnagyobb megnyúlása, és legfeljebb mekkora rugalmas energiával rendelkezik a rugó?
Adatok: \(\displaystyle D=16\) N/m, \(\displaystyle m=0{,}25\) kg, \(\displaystyle v_0=2\) m/s.
(3 pont)
G. 615. \(\displaystyle 30^\circ\)-os hajlásszögű, elég hosszú lejtőn gyorsulva csúszik lefelé egy vízzel félig telt tartály. Mekkora szöget zár be a víz felszíne a lejtő síkjával, ha a súrlódás elhanyagolható?
(3 pont)
G. 616. Egy vékony falú, elhanyagolható súlyú gimnasztikai labda sugara 30 cm, benne a levegő nyomása \(\displaystyle 1{,}1\cdot10^5\) Pa, a külső légnyomás \(\displaystyle 1{,}0\cdot10^5\) Pa. Mennyivel csökken a labda térfogata, amikor egy 50 kg tömegű személy teljes súlyával ránehezedik, ha ekkor a labda egy 10 cm sugarú körben érintkezik a padlóval? A levegő hőmérséklete állandó.
Közli: Radnai Gyula, Budapest
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2017. december 11-én LEJÁRT. |
P. 4970. Egy jármű \(\displaystyle A\) városból \(\displaystyle B\)-be megy. Útja első részén \(\displaystyle v_1\) az átlagsebessége, a hátralévőn pedig \(\displaystyle v_2\). Második útszakaszának hossza hányszorosa az elsőének, ha a teljes útra vonatkozó átlagsebessége a két részútra vonatkozó átlagsebességének
\(\displaystyle a)\) számtani közepe;
\(\displaystyle b)\) mértani közepe;
\(\displaystyle c)\) harmonikus közepe;
\(\displaystyle d)\) \(\displaystyle 1:k\) arányú súlyozott számtani közepe?
Közli: Zsigri Ferenc, Budapest
(4 pont)
P. 4971. \(\displaystyle 30^\circ\)-os hajlásszögű, elég hosszú lejtőn gyorsulva csúszik lefelé egy vízzel félig telt tartály. Mekkora szöget zár be a víz felszíne a lejtő síkjával, ha a tartály és a lejtő közötti súrlódási együttható 0,2?
Példatári feladat alapján
(4 pont)
P. 4972. Egy \(\displaystyle \ell\) hosszúságú, könnyű és nyújthatatlan fonál egyik végét felfüggesztjük, a másikat pedig egy kicsiny gyűrűhöz kötjük, amely súrlódásmentesen csúszhat egy – a felfüggesztési pont felett \(\displaystyle d<\ell\) magasságban található – vízszintes rúdon. Az ily módon elhelyezett fonálra kifeszített állapotban egy kicsiny csiga közvetítésével \(\displaystyle m\) tömegű súlyt akasztunk a rúd közvetlen közelében, majd a rendszert magára hagyjuk.
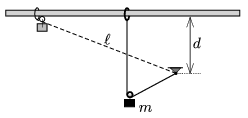
\(\displaystyle a)\) Mekkora lesz a test sebessége a pálya legalsó pontjában?
\(\displaystyle b)\) Milyen görbe mentén mozog a súly?
\(\displaystyle c)\) Mekkora erő feszíti a fonalat a pálya legalsó pontjánál?
Közli: Németh Róbert,
Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn.
(5 pont)
P. 4973. Baintner Géza (1892–1980) egyetemi előadásán szerepelt az a kísérlet, amikor három gumikötél Y alakban van összekötve, és az Y szimmetrikus végeit ellenkező fázisban rezegtetve, a keletkező két hullám kioltotta egymást, a harmadik ág nyugton maradt. Kérdés: Hová lett a két hullám energiája?
Marx György (1927–2002) feladata
(4 pont)
P. 4974. Targoncához erősített, hőszigetelő hengerben \(\displaystyle M=20\) kg tömegű, könnyen mozgó, hőszigetelő dugattyú \(\displaystyle V_0=50\) liter térfogatú, \(\displaystyle T_0=300\) K hőmérsékletű, \(\displaystyle p_0=10^5\) Pa nyomású levegőrészeket választ el. A targonca \(\displaystyle v=10\) m/s sebességgel halad egy fal felé, amellyel tökéletesen rugalmatlanul ütközik. Legfeljebb mekkora hőmérsékletet ér el a fal felőli részben lévő levegő a folyamat során?
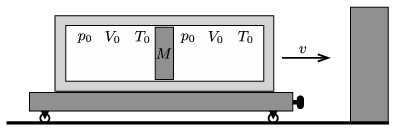
Közli: Holics László, Budapest
(5 pont)
P. 4975. Egy földi laboratóriumi kísérlet során az \(\displaystyle m\) tömegű, \(\displaystyle Q\) töltésű kicsiny testet vákuumban, \(\displaystyle B\) indukciójú, vízszintes irányú, homogén mágneses térben engedjük el. (Feltehetjük, hogy \(\displaystyle mg < QBc\), ahol \(\displaystyle c\) a fénysebesség.) A test mozgását addig vizsgáljuk, míg eléri legmélyebb helyzetét.
\(\displaystyle a)\) Mekkora lesz a test legnagyobb sebessége?
\(\displaystyle b)\) Milyen mélyre süllyed?
\(\displaystyle c)\) Mekkora átlagsebességgel mozog vízszintes irányban?
\(\displaystyle d)\) Mekkora a test gyorsulása pályájának legmélyebb pontján?
Közli: Simon Péter, Pécs
(5 pont)
P. 4976. Három kicsiny golyót egy egyenes mentén helyeztünk el úgy, hogy kezdetben nem mozognak, és a szomszédos golyók távolsága \(\displaystyle d\). A golyók tömege és töltése rendre \(\displaystyle m\), \(\displaystyle 2m\), \(\displaystyle 5m\), illetve \(\displaystyle q\), \(\displaystyle q\), \(\displaystyle 2q\).
\(\displaystyle a)\) Mekkora lesz a golyók távolsága és sebessége az indulást követő nagyon rövid \(\displaystyle t_0\) idő múlva?
\(\displaystyle b)\) Mekkora lesz a golyók sebessége elegendően hosszú idő múlva?
(Az elektrosztatikus erőkön kívül minden más erőhatás elhanyagolható.)
A Kvant nyomán
(5 pont)
P. 4977. Az ábrán látható kapcsolásban a kapcsoló zárása előtt a kondenzátorok töltetlenek. Egy adott pillanatban zárjuk a kapcsolót. (Az áramforrás belső ellenállásától, a vezetékek és az ellenállások kapacitásától, továbbá a körben lévő elemek induktivitásától tekintsünk el.)
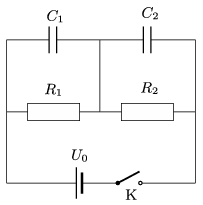
Ábrázoljuk vázlatosan a kondenzátorok feszültségét az idő függvényében!
Adatok: \(\displaystyle C_1=150~\mu\)F, \(\displaystyle C_2=50~\mu\)F, \(\displaystyle R_1=40~\rm k\Omega\), \(\displaystyle R_2=10~\rm k\Omega\), \(\displaystyle U_0=100\) V.
Nagy László (1931–1987) feladata
(5 pont)
P. 4978. Az ionrakéta hajtóművében pozitív töltésű nehézionokat gyorsítanak fel, ezek áramlanak ki a fúvókán keresztül, ettől gyorsul fel a rakéta. Ugyanekkor elektrongyorsítót is beszerelnek az ionrakétába, erre miért van szükség?
Némedi István (1932–1998) feladata
(3 pont)
P. 4979. A súlytalanság állapotában egy \(\displaystyle R\) sugarú, \(\displaystyle \alpha\) felületi feszültségű higanycsepp lebeg. Ha a cseppet gyenge, \(\displaystyle E_0\) térerősségű, homogén elektromos térbe helyezzük, a csepp a térerősség irányában kissé megnyúlik, alakja forgási ellipszoiddal közelíthető. Adjunk becslést, mekkora lesz a megnyúlt higanycsepp hossza.
Közli: Vigh Máté, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

