KöMaL Problems in Physics, September 2018
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on October 10, 2018. |
M. 379. Measure the height from which a retractable ballpoint click pen should be dropped from a vertical position in order that it is clicked on. When the tip of the pen is already out, from what height should it be dropped vertically in order that it is clicked off?
(6 pont)
 |
Problems with sign 'G'Deadline expired on October 10, 2018. |
G. 641. The mass of each pulley in the pulley system shown in the figure is 1 kg. What is the magnitude of the force \(\displaystyle F\) with which the monkey in the cage can be kept in equilibrium? The total mass of the monkey and the cage is 9 kg.
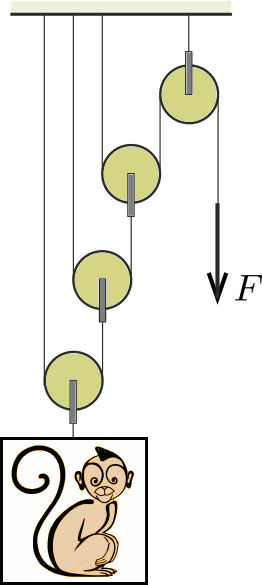
(3 pont)
solution (in Hungarian), statistics
G. 642. A wheel of radius \(\displaystyle R\) is rolling without slipping along the inner circumference of a circle of radius \(\displaystyle 2R\). What is the path of a point on the rim of the small wheel?
(3 pont)
solution (in Hungarian), statistics
G. 643. A bowl of water is placed on one of the plates of a beam scale, which is balanced. One of our fingers is immersed into the water, such that the bowl is not touched. Will the scale remain balanced or not, if \(\displaystyle a)\) not a drop of water flows out of the bowl; \(\displaystyle b)\) the bowl was full to the brim, and the water flows off the plate of the scale?
(3 pont)
solution (in Hungarian), statistics
G. 644. Four alike bulbs are connected as shown in the figure to a battery. Which one is the brightest? List them in the order of their luminous power.
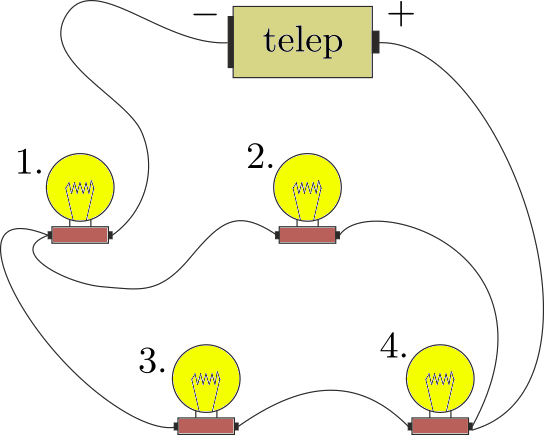
(3 pont)
 |
Problems with sign 'P'Deadline expired on October 10, 2018. |
P. 5045. An object falls freely on the Moon. The total height from which the object was dropped is \(\displaystyle n\) times greater than the distance covered by the object in the last second of its fall. Determine the height from which it was dropped and the time of the fall.
(4 pont)
solution (in Hungarian), statistics
P. 5046. A board of mass \(\displaystyle M\) was fixed symmetrically as shown in the figure. The masses of the fixed pulleys and the ropes, as well as friction in the shaft are negligible. (The objects of mass \(\displaystyle m\) are not glued to the board of mass \(\displaystyle M\).) At what \(\displaystyle m/M\) ratio will the system be in equilibrium?
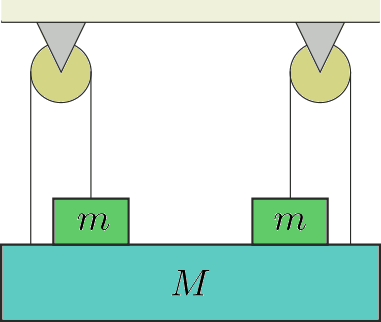
(3 pont)
solution (in Hungarian), statistics
P. 5047. The cart of mass \(\displaystyle M\) and the flat block of mass \(\displaystyle m\) on the cart are moving at a speed of \(\displaystyle v\) towards a compression spring fixed to a wall, and having a spring constant of \(\displaystyle D\). The coefficient of friction between the block and the cart is \(\displaystyle \mu\). \(\displaystyle a)\) Will the block slip or not when the collision occurs? \(\displaystyle b)\) How long does the collision last? Data: \(\displaystyle M=0.2\) kg, \(\displaystyle m=0.1\) kg, \(\displaystyle v=1\) m/s, \(\displaystyle D=4.4\) N/m, \(\displaystyle \mu=0.4\).
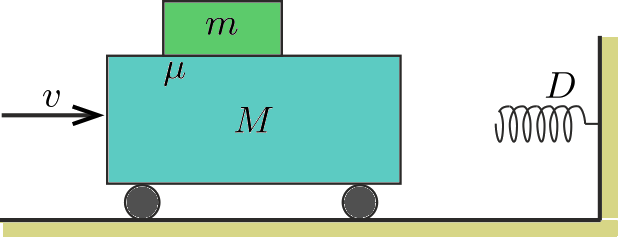
(4 pont)
solution (in Hungarian), statistics
P. 5048. Estimate the pressure difference in the tyre of a car between an ,,inner'' point next to the rim of the wheel, and an ,,outer'' point next to the tread area. The excess pressure of the tyre when the car is at rest is 2 bars, and the maximum allowed speed on the motorway is 130 km/h.
(4 pont)
solution (in Hungarian), statistics
P. 5049. To what minimum speed must a rocket be accelerated, in order that it reaches the Moon from the Earth? Compare this speed to the escape speed on Earth. (For the sake of simplicity, do not consider the motion of the Earth and the Moon.)
(5 pont)
solution (in Hungarian), statistics
P. 5050. There is some water and some water vapour above it in a closed container. What happens to the water if the water vapour is sucked out of the container, whilst the temperature of the water is kept constant, if this temperature is
\(\displaystyle a)\) 100.00 \(\displaystyle {}^\circ\)C;
\(\displaystyle b)\) 20.00 \(\displaystyle {}^\circ\)C?
(3 pont)
solution (in Hungarian), statistics
P. 5051. A sample of helium is taken through the processes shown in the figure. How much thermal energy is absorbed during the process?
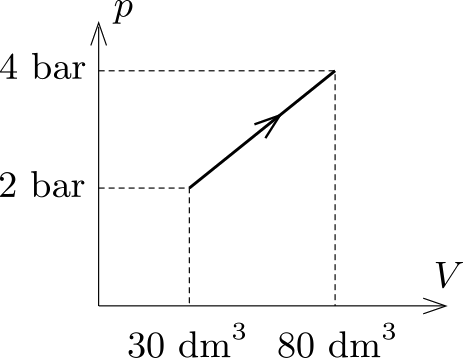
(4 pont)
solution (in Hungarian), statistics
P. 5052. There is a small grain under a 1.5 cm wide glass sheet. Where is the visible image of the grain, if the light rays are perpendicular to the surface of the sheet, and the refractive index of the glass is \(\displaystyle n=1.5\)?
(3 pont)
solution (in Hungarian), statistics
P. 5053. Determine the total luminosity of a star whose surface temperature is 7500 K, and whose diameter is 2.5 times bigger than that of the Sun. The surface temperature of the Sun is 5800 K, and express the luminosity of the star in terms of the luminosity of the Sun (which is considered to be 1).
(4 pont)
solution (in Hungarian), statistics
P. 5054. A nucleus of rest mass \(\displaystyle M\), which is initially at rest can absorb a gamma quantum of energy \(\displaystyle hf\). Determine the excitation energy of this nucleus in the process. (So by what amount does its rest energy increase in the process?)
(5 pont)
solution (in Hungarian), statistics
P. 5055. One end of a horizontally stretched rubber thread is moved periodically in the vertical direction, so transverse waves are travelling along the thread. A film is recorded about the motion of a small part of the thread, and three consecutive frames of this film are shown in the figure. In which direction does the energy propagate in the rope, from the left to the right or from the right to the left?
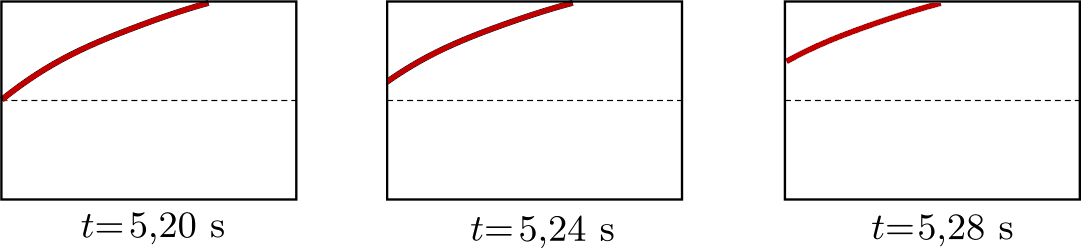
(6 pont)
Upload your solutions above.
