KöMaL Problems in Physics, March 2019
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on April 10, 2019. |
M. 385. When a relatively large obstacle having a horizontal (planar) face is placed under the water stream flowing from the kitchen tap, then the spreading water forms a circular area where it has a visible increase in its height. This is called the hydraulic jump. At a certain obstacle-tap distance, measure how the radius of the circle depends on the rate of water flow.
(6 pont)
 |
Problems with sign 'G'Deadline expired on April 10, 2019. |
G. 665. In this problem the motion of a small disc sliding along a horizontal frictionless surface of ice is investigated. A column, having a square-shaped cross section, emerges from the ice. The side of the square is 10 cm. The disc is attached to the column by means of a piece of 1.0 m long thread. The top view of the arrangement is shown in the figure. The disc is given an initial speed of \(\displaystyle v=1.0\) m/s. How much time elapses until the disc hits the column?

(3 pont)
solution (in Hungarian), statistics
G. 666. The figure shows the sketch of the structure of an amusement park ride. The big cylinder-shaped pole at the centre is rotating uniformly. By four horizontal struts circular ``gondolas'' are attached to the pole and move around it. At the centre of each gondola a horizontal disc is fixed to the gondola such that the symmetry axis of the disc coincides with the vertical shaft of the gondola about which it can be rotated. These discs on the gondolas are connected by transmission belts to disc \(\displaystyle K\), which is attached to the pole at the centre of the structure. Disc \(\displaystyle K\) is fixed, and not rotating at all. (For clarity reasons only one of the transmission belts was drawn in the figure.)
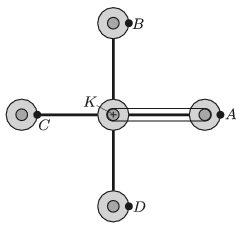
At points \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) and \(\displaystyle D\) there is a passenger in each gondola. What is the path of each passenger? How does the distance between them change during the rotation? (The structure is rotating in the horizontal plane and all the rotational axes are vertical.)
(4 pont)
solution (in Hungarian), statistics
G. 667. There is an aluminium cube of edge 10 cm on a table. What is the pressure due to the cube on the table? By what percent does this pressure change when the temperature of the cube is increased from \(\displaystyle 20\;{}^\circ\)C to \(\displaystyle 100\;{}^\circ\)C? Does it increase or decrease?
(3 pont)
solution (in Hungarian), statistics
G. 668. Watch the following YouTube video: https://www.youtube.com/watch?v=hvqQ1XG1aQE, make your own button spinner (buzzer) from a button of appropriate size and a piece of thin thread, and then try it. Why does the button begin to spin fast?
(3 pont)
 |
Problems with sign 'P'Deadline expired on April 10, 2019. |
P. 5111. A ping-pong ball was thrown vertically upward. Which takes longer, the upward or the downward motion of the ball? (Consider air drag.)
(3 pont)
solution (in Hungarian), statistics
P. 5112. From a wall of height \(\displaystyle H\) a snowball was thrown at an initial speed of \(\displaystyle v_0\) and at an angle of \(\displaystyle \alpha\) with respect to the horizontal. A child, who was at a distance of \(\displaystyle s\) from the wall, began to run at the same moment when the snowball was thrown. What was the initial direction and speed of the child, if he ran at a constant speed along a straight line and the snowball hit him? (Air drag is negligible.) Both the motions of the child and the snowball are in a vertical plane, which is perpendicular to the wall.
Data: \(\displaystyle H=45\) m, \(\displaystyle s=21\) m, \(\displaystyle v_0=5\) m/s, \(\displaystyle \alpha=30^\circ\).
(4 pont)
solution (in Hungarian), statistics
P. 5113. An 80-kg man is walking up in a tower built on the Equator of the Earth. How much does the apparent weight of the man decrease in each metre of ascent?
(4 pont)
solution (in Hungarian), statistics
P. 5114. Ending at the rim of the table there is a slope of angle of elevation of \(\displaystyle \alpha\), from which a uniform density rectangular block of length \(\displaystyle \ell\) and of height \(\displaystyle d\) is sliding down. By what length does the block move further from the end of the table until it tilts, if
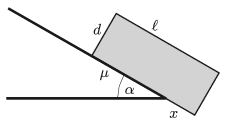
\(\displaystyle a)\) friction between the slope and the block is negligible;
\(\displaystyle b)\) the coefficient of kinetic friction between the slope and the block is \(\displaystyle \mu\) (\(\displaystyle 0<\mu<\tan\alpha\), and \(\displaystyle \mu d<\ell\))?
(5 pont)
solution (in Hungarian), statistics
P. 5115. The mass of an exoplanet, whose mass distribution has a spherical symmetry, is four times that of the Earth, and the acceleration due to gravity on the surface of the – non-rotating – planet is twice of the gravitational acceleration on the Earth.
\(\displaystyle a)\) What is the radius of the exoplanet, and what is its average density?
\(\displaystyle b)\) At what speed should an object be projected in order that it undergoes uniform circular motion right above the surface of the exoplanet?
(5 pont)
solution (in Hungarian), statistics
P. 5116. Two spherical shells of inner radius \(\displaystyle R\) and \(\displaystyle 3R\) are placed far from each other. They are made of some thin conducting material, the width of their wall \(\displaystyle d\) is thin: \(\displaystyle d\ll R\). At the centres of the spheres there are charges of \(\displaystyle 2Q\) and \(\displaystyle Q\). What is the minimum work which should be done in order to interchange the charges? (There are small holes on the walls.)
(5 pont)
solution (in Hungarian), statistics
P. 5117. A golden wedding ring is positioned such that the magnetic induction vector of the Earth is parallel to the ring. The ring is rotated uniformly by \(\displaystyle 180^\circ\) in 1 second. The axis of rotation is in the plane of the ring, and
\(\displaystyle a)\) parallel to the magnetic induction vector;
\(\displaystyle b)\) perpendicular to the magnetic induction vector.
In which case do we have to do more work, while the ring is turned? Estimate the difference between the values of the performed work in the two cases.
(5 pont)
solution (in Hungarian), statistics
P. 5118. A pair of parallel rails of negligible resistance is fixed to a slope of angle of elevation of \(\displaystyle \alpha=30^\circ\), at a distance of \(\displaystyle \ell=10\) cm from each other. A power supply of constant voltage of \(\displaystyle U_0\) is connected across the lower ends of the rails. A horizontal metal rod of mass \(\displaystyle M=30\) g and of resistance \(\displaystyle R=0.2~\Omega\) is placed perpendicularly to the rails. The rod can move frictionlessly. A piece of thread, which is parallel to the rails, is attached to the middle of the rod, and looped over a massless pulley. An object of mass \(\displaystyle m=50\) g is hung to the vertical end of the thread. The arrangement is in vertically upward uniform magnetic field of induction \(\displaystyle B=0.5\) T.
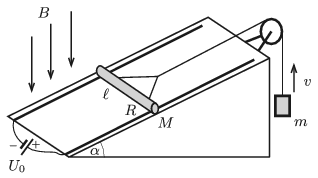
What should the voltage of the power supply be in order that the object of mass \(\displaystyle m\) moves
\(\displaystyle a)\) vertically upward,
\(\displaystyle b)\) vertically downward at a constant speed of \(\displaystyle v=10\) m/s?
(5 pont)
solution (in Hungarian), statistics
P. 5119. Newton in his famous crucial experiment (experimentum crucis) separated a beam of white light into colours by means of a prism. Then he combined the spectrum back into white light. Is it possible to form a spectrum from a beam of white light and then combine it back into white light by means of the system of prisms used as shown in the figure?
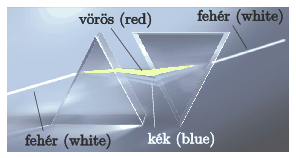
(4 pont)
solution (in Hungarian), statistics
P. 5120. When radiotherapy is applied, the tumour is exposed to a certain dose (absorbed energy per unit mass) of radiation, such that the surrounding healthy tissues do not absorb a too large dose. Investigate this problem by using the following simple model: the patient's head is considered to be a uniform sphere of radius 8 cm. The small tumour is located at the centre of the sphere and is radiated by beams of \(\displaystyle \gamma\) photons, having the same intensity. The radiation beams are aimed from the direction of five different diameters. The intensity (power per unit area) of the radiation beam is decreasing exponentially as the beam passes the tissues in the sphere, in accordance with the following equation: \(\displaystyle I(x)=I_0{\rm e}^{-\mu x}\).(The distance of \(\displaystyle x_0=\ln 2/\mu\) is called the half-value layer; its numerical value depends on the energy of the photons and the material of the absorbing medium. E.g. for photons of energy 2.5 MeV it is \(\displaystyle x_0=23\) cm in water.)

Two different types of radiation can be applied: either \(\displaystyle \gamma\)-photons of energy 1 MeV emitted by a source of \(\displaystyle ^{60}\rm Co\), for which \(\displaystyle \mu=0.07~\rm cm^{-1}\), or \(\displaystyle \gamma\)-photons of energy 6 MeV, which can be generated by a particle accelerator, here \(\displaystyle \mu=0.028~\rm cm^{-1}\).
Which radiation spares more the healthy tissues, that is, which one results a smaller dose at the surface of the sphere? What is the value of the dose next to the surface of the sphere if the necessary dose value at the tumour is \(\displaystyle D\)?
(5 pont)
solution (in Hungarian), statistics
P. 5121. Three small alike balls (denoted by the letters \(\displaystyle A\), \(\displaystyle B\) and \(\displaystyle C\)) of mass \(\displaystyle m\) are attached by means of two negligible-mass rods of length \(\displaystyle \ell\), such that one of the rods joins balls \(\displaystyle A\) and \(\displaystyle B\), whilst the other joins balls \(\displaystyle B\) and \(\displaystyle C\). At ball \(\displaystyle B\) there is an articulate joint so the angle between the rods can be freely varied. The system is at rest in weightlessness, and the three balls are collinear. Then at an instant an initial velocity of \(\displaystyle v_0\) is given to ball \(\displaystyle A\) perpendicularly to the rods. What are the forces in the rods at the moment right after starting ball \(\displaystyle A\)?
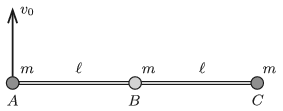
(6 pont)
Upload your solutions above.
