KöMaL Problems in Mathematics, May 2019
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'C'Deadline expired on June 11, 2019. |
C. 1546. Find the integer solutions of the equation \(\displaystyle (x-8)(x-10)=2^y\).
(American competition problem)
(5 pont)
solution (in Hungarian), statistics
C. 1547. Let \(\displaystyle K\) denote the midpoint of side \(\displaystyle EF\) in a regular hexagon \(\displaystyle ABCDEF\). Find the point \(\displaystyle L\) on the broken line \(\displaystyle ABCD\) for which the area of triangle \(\displaystyle AKL\) is \(\displaystyle \frac25\) of the area of the hexagon.
Based on a problem by T. Bakos
(5 pont)
solution (in Hungarian), statistics
C. 1548. Ann selects a few fields of a \(\displaystyle 3\times 3\) table. Then row by row and column by column, she tells Bill how many selected fields there are in that row or column. In how many different ways may Ann select her fields so that Bill cannot find out from the given information which fields she selected?
(5 pont)
solution (in Hungarian), statistics
C. 1549. Let \(\displaystyle F\) be the midpoint of a line segment \(\displaystyle AB\), and let \(\displaystyle Z\) be an arbitrary point on line segment \(\displaystyle AF\). Draw a perpendicular to \(\displaystyle AB\) at \(\displaystyle F\), and mark a distance \(\displaystyle FX=FA\) on it. Draw another perpendicular to \(\displaystyle AB\) at \(\displaystyle B\), and mark a distance \(\displaystyle BY=AZ\) on it such that \(\displaystyle X\) and \(\displaystyle Y\) lie on the same side of line \(\displaystyle AB\). What may be the size of the angle \(\displaystyle XZY\)?
Proposed by L. Surányi, Budapest
(5 pont)
solution (in Hungarian), statistics
C. 1550. Find all positive integers \(\displaystyle n\) satisfying \(\displaystyle n\cdot(1!+2!+3!+\cdots+n!)=(n+1)!\).
(5 pont)
solution (in Hungarian), statistics
C. 1551. In a triangle \(\displaystyle ABC\), the lengths of medians \(\displaystyle AD\) and \(\displaystyle BE\) are 3 cm and 6 cm, respectively, and the area of the triangle is \(\displaystyle 3\sqrt{15}\, \mathrm{cm}^2\). Determine the length of the third median, given that it is different from the other two.
(5 pont)
solution (in Hungarian), statistics
C. 1552. Prove that if \(\displaystyle 0<a<1\) and \(\displaystyle 0<b<1\) then \(\displaystyle \log_a\frac{2ab}{a+b}\cdot\log_b\frac{2ab}{a+b}\ge 1\).
Proposed by S. Róka, Nyíregyháza
(5 pont)
 |
Problems with sign 'B'Deadline expired on June 11, 2019. |
B. 5030. Prove that every integer greater than \(\displaystyle 1\) can be represented as a sum of numbers of the form \(\displaystyle 2^p\cdot 3^q\) greater than \(\displaystyle 1\) such that no term of the sum is a divisor of another term. (For example, \(\displaystyle 23=9+8+6\), \(\displaystyle 11=9+2\) or \(\displaystyle 12=12\).)
A problem of Paul Erdős
(4 pont)
solution (in Hungarian), statistics
B. 5031. Let \(\displaystyle F\) be a point on the extension of side \(\displaystyle AD\) of parallelogram \(\displaystyle ABCD\) beyond vertex \(\displaystyle D\). Line segment \(\displaystyle BF\) intersects side \(\displaystyle CD\) at \(\displaystyle G\) and diagonal \(\displaystyle AC\) at \(\displaystyle E\). Show that \(\displaystyle \frac{1}{BE}=\frac{1}{BG}+\frac{1}{BF}\).
(3 pont)
solution (in Hungarian), statistics
B. 5032. In the interior of an isosceles triangle, what is the locus of points for which the distance from the base is the geometric mean of the distances from the legs?
(4 pont)
solution (in Hungarian), statistics
B. 5033. The \(\displaystyle \binom{n+1}{2}\) numbers \(\displaystyle a_{1,1}, a_{1,2}, \ldots, a_{1,n}, a_{2,1}, a_{2,2}, \ldots, a_{2,n-1}, \ldots, a_{k,1}, \ldots, a_{k,n+1-k}, \ldots, a_{n,1}\) are called an inverted Pascal pyramid of order \(\displaystyle n\) if \(\displaystyle a_{k,j}=a_{k-1,j} + a_{k-1,j+1}\) for an arbitrary \(\displaystyle 2 \le k \le n\) and \(\displaystyle 1 \le j \le n+1-k\). An example of an inverted Pascal pyramid of order 3 is shown below:
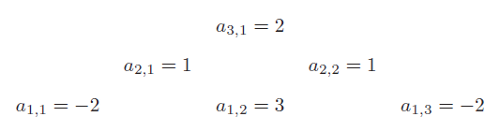
Let \(\displaystyle s_k\) denote the sum of the numbers in row \(\displaystyle k\) of the pyramid, that is, \(\displaystyle s_k = a_{k,1} + a_{k,2} + \cdots + a_{k,n+1-k}\). A pyramid is said to have a sign change in row \(\displaystyle k\) (\(\displaystyle k>1\)) if \(\displaystyle s_{k-1} \cdot s_k <0\). Given the value of \(\displaystyle n\), what is the largest possible \(\displaystyle k\) if a pyramid of order \(\displaystyle n\) has sign changes in rows 2, 3, \(\displaystyle \ldots\), \(\displaystyle k\), but no sign change in row \(\displaystyle (k+1)\)? (In the example above, \(\displaystyle k=2\) since \(\displaystyle s_1 \cdot s_2 = -2 <0\) but \(\displaystyle s_2 \cdot s_3 = 4 >0\).)
(5 pont)
solution (in Hungarian), statistics
B. 5034. Prove that if none of the angles \(\displaystyle \alpha\), \(\displaystyle \beta\), \(\displaystyle \gamma\), \(\displaystyle \delta\) of a convex quadrilateral are right angles then \(\displaystyle \tan \alpha+\tan \beta+\tan \gamma+\tan \delta=\tan \alpha\cdot\tan \beta\cdot\tan \gamma\cdot \tan \delta(\cot \alpha+\cot\beta+\cot\gamma+\cot\delta)\).
A problem of J. Surányi
(3 pont)
solution (in Hungarian), statistics
B. 5035. The edges of a complete graph on \(\displaystyle n\ge 8\) vertices are coloured in two colours. Prove that the number of cycles formed by four edges of the same colour is more than \(\displaystyle \frac{{(n-5)}^4}{64}\).
Based on a problem proposed by M. Pálfy, Budapest
(6 pont)
solution (in Hungarian), statistics
B. 5036. From a point \(\displaystyle M\), two tangents are drawn to a right-angled hyperbola of centre \(\displaystyle O\). One tangent intersects an asymptote at point \(\displaystyle P\), and the other tangent intersects the other asymptote at point \(\displaystyle Q\). Prove that line \(\displaystyle OM\) bisects the line segment \(\displaystyle PQ\).
(5 pont)
solution (in Hungarian), statistics
B. 5037. A polyhedron \(\displaystyle P\) is divided into the smaller polyhedra \(\displaystyle P_1, \ldots, P_k\) and also divided into the smaller polyhedra \(\displaystyle Q_1, \ldots, Q_k\) such that the polyhedra \(\displaystyle P_i\) and \(\displaystyle Q_i\) are congruent for all \(\displaystyle i=1, \ldots, k\). Show that it is possible to select some points in the interior of \(\displaystyle P\) such that there are the same number of points (at least one) in the interior of polyhedra \(\displaystyle P_i\) and \(\displaystyle Q_i\) for all \(\displaystyle i=1, \ldots, k\). (The position of each polyhedron is fixed in the space.)
(6 pont)
 |
Problems with sign 'A'Deadline expired on June 11, 2019. |
A. 752. Let \(\displaystyle k\), \(\displaystyle s\) and \(\displaystyle n\) be positive integers such that \(\displaystyle s<(2k+1)^2\), and let \(\displaystyle R\) be the set of lattice points \(\displaystyle (x,y)\) in the plane, satisfying \(\displaystyle 1\le x,y\le n\). On the grid \(\displaystyle R\) we perform the following procedure. Initially, we colour one point of \(\displaystyle R\) green; all other points in \(\displaystyle R\) are coloured white. On every move, we choose a square \(\displaystyle S\), consisting of \(\displaystyle {\color{red}(2k+1)\times(2k+1)}\) lattice points in such a way that the center of \(\displaystyle S\) is green and it contains at least \(\displaystyle s\) white points; then we re-colour \(\displaystyle s\) white points of \(\displaystyle S\) to green. We repeat this step as long as there is a suitable square \(\displaystyle S\).
We say that the number \(\displaystyle s\) is \(\displaystyle k\)-sparse, if there exists a positive real number \(\displaystyle C\) such that, for every \(\displaystyle n\), for every choice of the initial green point, and for every valid sequence of moves, the total number of green points in the grid cannot exceed \(\displaystyle Cn\).
Determine the least \(\displaystyle k\)-sparse positive integer \(\displaystyle s\) in terms of \(\displaystyle k\).
Proposed by: Nikolai Beluhov (Stara Zagora, Bulgaria)
(7 pont)
A. 753. Let \(\displaystyle a\) be an integer, and let \(\displaystyle p\) be a prime divisor of \(\displaystyle a^3+a^2-4a+1\). Show that there is an integer \(\displaystyle b\) such that \(\displaystyle p\equiv b^3\pmod{13}\).
(7 pont)
A. 754. Let \(\displaystyle P\) be a point inside the acute triangle \(\displaystyle ABC\), and let \(\displaystyle Q\) be the isogonal conjugate of \(\displaystyle P\). Let \(\displaystyle L\), \(\displaystyle M\) and \(\displaystyle N\) be the midpoints of the shorter arcs \(\displaystyle BC\), \(\displaystyle CA\) and \(\displaystyle AB\) of the circumcircle of \(\displaystyle ABC\), respectively. Let \(\displaystyle X_A\) be the intersection of ray \(\displaystyle LQ\) and circle \(\displaystyle PBC\), let \(\displaystyle X_B\) be the intersection of ray \(\displaystyle MQ\) and circle \(\displaystyle PCA\), and let \(\displaystyle X_C\) be the intersection of ray \(\displaystyle NQ\) and circle \(\displaystyle PAB\). Prove that \(\displaystyle P\), \(\displaystyle X_A\), \(\displaystyle X_B\) and \(\displaystyle X_C\) are concyclic or coincide.
Proposed by: Gustavo Cruz (São Paulo)
(7 pont)
Upload your solutions above.
