KöMaL Problems in Physics, March 2020
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on April 14, 2020. |
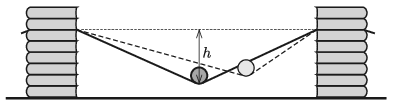
M. 394. Make an approximately 80 cm long paper strip, and fix its ends at the same height to some moveable stands. Place a small cylinder-shaped tin can on the middle of the strip such that the tin pulls down the strip a little. Then displace the tin always by the same amount (approximately 20 cm), and then release it without any initial speed, and let it roll freely. Measure the period of the (damped) periodic motion of the tin, as a function of the sag of the strip \(\displaystyle h\) in the case of
\(\displaystyle a)\) a full tin can;
\(\displaystyle b)\) an empty tin can.
(6 pont)
 |
Problems with sign 'G'Deadline expired on April 14, 2020. |
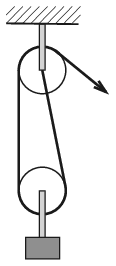
G. 701. What is the ratio of the number of revolutions of the two pulleys shown in the figure, if their radius is the same? (The threads between the pulleys can be considered vertical.)
(3 pont)
solution (in Hungarian), statistics
G. 702. A disc-shaped permanent magnet of a mass of 80 g clings to a vertical iron sheet. The flat disc can be slid vertically downwards by applying a force of 2 N. With what force can the magnet be moved upwards? What is the magnitude and the direction of the force which should be applied in order to move the disc horizontally? (The applied force is parallel to the plane of the sheet in all cases.)
(4 pont)
solution (in Hungarian), statistics
G. 703. How can we determine the internal resistance of a durable battery by using a digital voltmeter (which can be considered ideal) and a resistor of known resistance? (Wires can also be used.)
(3 pont)
solution (in Hungarian), statistics
G. 704. When Torricelli's experiment is carried out at sea level, then the mercury column is 76 cm high. However, on a very high hill the height of the mercury is only 40 cm. How high is the hill?
(3 pont)
 |
Problems with sign 'P'Deadline expired on April 14, 2020. |
P. 5208. A basketball of mass 0.6 kg bounces to a height of 0.57 m when it is dropped form a height of 1.05 m.
\(\displaystyle a)\) What is the mechanical energy loss due to the collision with the ground?
\(\displaystyle b)\) What is the ratio of the speed at which the basketball bounced back to the speed of the ball when it reached the ground? (This ratio is called the coefficient of restitution.)
\(\displaystyle c)\) In order to compensate the energy loss, players usually dribble the basketball, during which they push the ball downwards for a short while. Suppose a player pushes the ball along a distance of 0.08 m, starting it at a height of 1.05 m. What is the average force exerted by the player if the ball bounces back to a height of 1.05 m?
(4 pont)
solution (in Hungarian), statistics
P. 5209. In the pulley system shown in the figure the fixed pulley at the top has a radius of 15 cm, whilst the radius of the moveable pulley at the bottom is 25 cm. Each of the moveable pulleys turns 15 whole revolutions in a minute, and the rotational speeds of the fixed pulleys are also equal. (The threads between the pulleys can be considered vertical.)
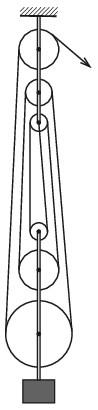
\(\displaystyle a)\) What is the radius of each of the other pulleys?
\(\displaystyle b)\) What is the number of revolutions of the fixed pulleys?
(4 pont)
solution (in Hungarian), statistics
P. 5210. The crew of the spacecraft Apollo 11 (Neil Armstrong, Edwin Aldrin és Michael Collins) performed the first landing on the Moon. The spacecraft was launched from the Kennedy Space Center on July 16, 1969.
\(\displaystyle a)\) Apollo 11 was launched by a Saturn V rocket, which had a thrust of \(\displaystyle 34\,000\) kN. The total mass of the spacecraft and the rocket after a few seconds of the launch was 2.8 millions of kilograms. What was the acceleration of the spacecraft at that time?
\(\displaystyle b)\) The spacecraft left the Earth orbit on July 16 at 16:22, and after travelling around \(\displaystyle 380\,000\) km, it entered lunar orbit on July 19 at 17:21. What was the approximate average speed of the spacecraft while it travelled from the Earth to the Moon?
(4 pont)
solution (in Hungarian), statistics
P. 5211. At what speed should a small object, being at rest at the starting point of a horizontal straight track of length \(\displaystyle 2L\), be pushed in order that after sliding along the vertical semicircular path of radius \(\displaystyle R\) at the end of the straight track it hit the midpoint of the horizontal track?
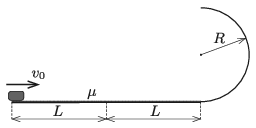
The coefficient of kinetic friction along the horizontal track is \(\displaystyle \mu\), the circular track is frictionless.
Data: \(\displaystyle L=2\) m; \(\displaystyle R=0.5\) m; \(\displaystyle \mu=0.4\).
(4 pont)
solution (in Hungarian), statistics
P. 5212. There is a simple pendulum suspended above a horizontal tabletop at a height of \(\displaystyle h\). The bob of the simple pendulum of length \(\displaystyle \ell>h\) is released without initial speed from the position at which the thread is horizontal. The bob at the end of the thread bounces on the table \(\displaystyle n\) times such that at the last bounce the thread just gets tight, and the pendulum swings forward. Determine the ratio of \(\displaystyle h\) to \(\displaystyle \ell\).
(The collisions are totally elastic, air resistance is negligible and the thread does not disturb the motion of the bob.)
(4 pont)
solution (in Hungarian), statistics
P. 5213. There is a sample of air, having a relative humidity of 30%, in a container. By what factor can the pressure of the air be increased, when the gas is compressed at constant temperature, if the condensation of water should be avoided.
(4 pont)
solution (in Hungarian), statistics
P. 5214. When Torricelli's experiment is carried out at sea level, then the mercury column is 76 cm high. However, on a very high hill the height of the mercury is only 40 cm. What is the magnitude of the vertically upward force that we have to apply in order to hold the tube at rest on the high mountain?
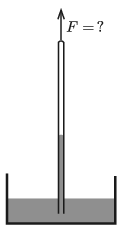
The inner diameter of the tube is 1 cm, its total length is \(\displaystyle 110~\)cm, from which 10 cm is immersed into the mercury. The mass of a 1 cm-long part of the tube is 1 g, and the mass of its cover at its top is 5 g. (The density of glass is 2.6 g/cm\(\displaystyle {}^3\).)
(5 pont)
solution (in Hungarian), statistics
P. 5215. The base of a warehouse is a square, and its walls are built from bricks of width 40 cm. \(\displaystyle \frac34\) of the surface of the wall is covered with 10 cm-thick heat insulating material, whilst \(\displaystyle \frac14\) of the surface of the wall is covered with 20 cm-thick heat insulating material. The thermal conductivity of brick is ten times as big as that of the heat insulating material. If the walls of the warehouse were covered uniformly with a layer of insulating material of thickness \(\displaystyle d\), the two types of insulation would result in the same effect in terms of heat propagation. What is the value of \(\displaystyle d\)?
(4 pont)
solution (in Hungarian), statistics
P. 5216. In a vertical cylinder, below a heavy piston, there is a sample of air of quantity of \(\displaystyle n\) moles at a temperature of \(\displaystyle T_0\). The container and the piston are well insulated and there is vacuum outside. The piston is slowly raised, and when a work of \(\displaystyle W\) was done, the piston is released. The piston begins to swing, but after a while it stops (because of the internal friction of the air).
What will the temperature of the air at the new equilibrium position be? How does this result change if the piston is not raised, but pushed down, while \(\displaystyle W\) work is done, and then it is suddenly released?
(5 pont)
solution (in Hungarian), statistics
P. 5217. The radioactive carbon-14 isotope is constantly produced in the atmosphere by the cosmic rays. Nonetheless, the amount of \(\displaystyle {}^{14}\mathrm{C}\) on the Earth is constant, because at a height of 5-9 km, as a result of the reaction \(\displaystyle \mathrm{n}+{}^{14}\mathrm{N}~\rightarrow~ {}^{14}\mathrm{C}+\mathrm{p}\), an average of \(\displaystyle 17\,600\) \(\displaystyle {}^{14}\mathrm{C}\) isotopes are produced in each second on each square metre – projected to the surface of the Earth. The half-life of the isotope is 5730 years.
Estimate how many tons of \(\displaystyle {}^{14}\mathrm{C}\) are present on the Earth.
(4 pont)
solution (in Hungarian), statistics
P. 5218. At the origin of a Cartesian coordinate system there is a small ``point-like'' compass needle, pointing in the direction of the \(\displaystyle x\) axis. The equation of one of its magnetic field line is \(\displaystyle r=r_0\sin^2\varphi\), where \(\displaystyle r\) and \(\displaystyle \varphi\) are the polar coordinates of a point on the field line.
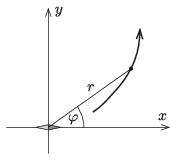
\(\displaystyle a)\) Write down the equation of the field line in terms of the \(\displaystyle x\) and \(\displaystyle y\) coordinates, if \(\displaystyle r_0=3\) metres.
\(\displaystyle b)\) At which points of the field line is the magnetic induction (magnetic flux density) perpendicular to the needle?
(6 pont)
Upload your solutions above.
