KöMaL Problems in Physics, April 2020
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on May 11, 2020. |
M. 395. Measure the rate of airflow of a hair dryer at different speed settings.
(6 pont)
 |
Problems with sign 'G'Deadline expired on May 11, 2020. |
G. 705. Two balls are released from an airship floating at a great height. Which ball falls faster, if
\(\displaystyle a)\) they have the same size, but different weights;
\(\displaystyle b)\) they have the same weight, but different sizes?
(3 pont)
solution (in Hungarian), statistics
G. 706. The docudrama titled Apollo 13 is about the happily ended accident of the spacecraft, occurred in 1970. The scenes depicting weightlessness were recorded in a Boeing KC-135 air-plane (belonging to NASA) in 612 short, 23 second-long parts. In order to create the ``zero gravity'' for each of these short parts the plane flew along a parabolic path. What was the smallest speed of the plane during the zero gravity period of the flights if the angle between the horizontal and tangent to the parabolic path of the plane both at he beginning and at the end of the zero gravity manoeuvre was \(\displaystyle 45^\circ\)?
(4 pont)
solution (in Hungarian), statistics
G. 707. Sam and Sarah are jogging along a straight path at constant speed. Sam's speed is 3 m/s and Sara's speed is 2 m/s. Pluto, their dog, is running back and forth between them. Initially Sarah is 20 m ahead Sam. Pluto is a ``miraculous'' dog, because he can run between them at a constant speed of 4 m/s such that all his turns are immediate. Considering Pluto's arbitrary initial location and direction of running, determine the smallest and greatest values of both the distance covered and the displacement of the dog until Sam and Sarah meet.
(4 pont)
solution (in Hungarian), statistics
G. 708. Ben ran into a mirrored labyrinth of an amusement park, and hid at point \(\displaystyle B\). Can his mother, who is looking for Ben standing at point \(\displaystyle A\), see him? The plan of the mirrored labyrinth of the amusement park is shown in the figure. The thick lines represent mirrors with reflexive surfaces at both of their sides.
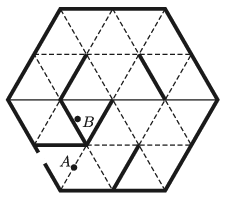
(4 pont)
 |
Problems with sign 'P'Deadline expired on May 11, 2020. |
P. 5219. There is a shadoof in the middle of a meadow in a plain. Its vertical pole has half the length of its horizontal beam. Reaching the rim of the meadow, the shadoof is at a distance of 100 m from us towards the north. Observing the shadoof from the rim of the meadow the angle subtended by its vertical pole is \(\displaystyle 2.3^\circ\). Our eyes are at a height of 165 cm, the horizontal beam is east–west and is supported by the pole at its centre.
We walk towards the shadoof at a constant speed of 1 m/s. Calculate and sketch how the angle subtended by the shadoof change over time as we walk from the rim of the meadow to the shadoof until we reach it.
(4 pont)
solution (in Hungarian), statistics
P. 5220. A compressed spring, which is tied with a piece of thread, is placed between two carts of masses \(\displaystyle M\) and \(\displaystyle 2M\) such that it is fixed to only one of the carts. This system is placed to a horizontal frictionless tabletop and given an initial speed of \(\displaystyle v_0\). After some time the thread breaks, and because of this one of the carts stops.
\(\displaystyle a)\) At what speed does the other cart move further?
\(\displaystyle b)\) How much energy was stored in the spring?
(4 pont)
solution (in Hungarian), statistics
P. 5221. A frictionless track is built for a small (point-like) toy car. The initial part of the track is horizontal, and then it continues in a vertical circular loop of radius \(\displaystyle r\), and horizontal again after the loop is closed. Let \(\displaystyle v\) be the least initial speed of the toy car at which it must be started in order that it just go along the circular loop. What fraction of this speed \(\displaystyle v\) should be given to the toy car in order that after leaving the loop it strike the track exactly at the opposite point of the circle?
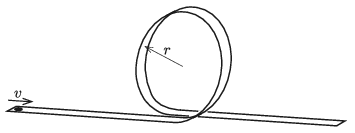
(5 pont)
solution (in Hungarian), statistics
P. 5222. Two solid rubber balls, made of high-quality rubber, are placed on the top of one another as shown in the figure, and then they are released from a height of \(\displaystyle h\). The collisions occur as follows: first the bottom ball of mass \(\displaystyle M\) collides with the ground totally elastically, then after a very short time the ball that bounced back from the ground collides totally elastically with the upper ball of mass \(\displaystyle m\).
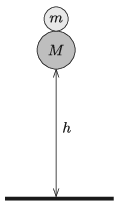
\(\displaystyle a)\) What is the ratio of \(\displaystyle m/M\) in the case when the total initial potential energy of the balls is converted to the energy of the upper ball? How high will the upper ball go up in this case?
\(\displaystyle b)\) What is the ratio of \(\displaystyle m/M\) in the case when the upper ball bounces to the greatest possible height and what is this height?
\(\displaystyle c)\) At what ratio of \(\displaystyle m/M\) can the above description of the collisions be applied? What happens for example at the mass ratio of \(\displaystyle k = m/M = 3\)?
(The collisions are momentary. The size of the balls is much smaller than the height \(\displaystyle h\).)
(5 pont)
solution (in Hungarian), statistics
P. 5223. Four alike balls, each of which has a weight of 30 N, are placed to the horizontal table into a frame – which has a shape of an equilateral-triangle-based right prism – as shown in the figure. Calculate the forces at the contact points if the side of the triangle is 15 cm, and the diameter of a ball is 5 cm. (Friction is negligible.)
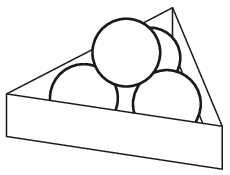
(5 pont)
solution (in Hungarian), statistics
P. 5224. In a swimming pool only the lights built in the vertical walls of the pool are turned on as dusk falls. The lights are 1 metre below the surface of the water. Someone stands 3 metres from the wall in front of a lamp such that his or her eyes are at a height of 30 cm above the water. How far from the wall does he or she observe a light spot on the surface of the water?
(5 pont)
solution (in Hungarian), statistics
P. 5225. There is 5 litres water at a temperature of \(\displaystyle 20\;{}^\circ\)C in a stockpot of base area 10 dm\(\displaystyle {}^2\). The density of water is 998 kg/m\(\displaystyle {}^3\). The water is heated to \(\displaystyle 80\;{}^\circ\)C. The coefficient of volume expansion of water can be considered constant between the temperature values of \(\displaystyle 20\;{}^\circ\)C and \(\displaystyle 80\;{}^\circ\)C, and it is \(\displaystyle \beta_\text{water}=4\cdot10^{-4}\) 1/K. The pot is made of stainless steel whose coefficient of volume expansion is \(\displaystyle \beta_\text{steel}=5\cdot10^{-5}\) 1/K. Neglect the vaporization of water.
\(\displaystyle a)\) What is the initial hydrostatic pressure at the bottom of the pot? How much does this value change during the heating?
\(\displaystyle b)\) How much does the level of water change due to the heating?
(4 pont)
solution (in Hungarian), statistics
P. 5226. Two metal rods of lengths \(\displaystyle \ell_1\) and \(\displaystyle \ell_2\), of thermal conductivity of \(\displaystyle \lambda_1\) and \(\displaystyle \lambda_2\), and having the same cross section are both covered with thermal insulating sleeves, and put together such that they form a single rod of length \(\displaystyle \ell_1+\ell_2\). The temperature values at the the two ends are adjusted to the values of \(\displaystyle T_1\) and \(\displaystyle T_2\).
\(\displaystyle a)\) What is the temperature of the rods at their contact points?
\(\displaystyle b)\) Sketch the temperature of the rod as a function of the position along the rod.
Data: \(\displaystyle \ell_1=65\) cm, \(\displaystyle \ell_2=40\) cm, \(\displaystyle \lambda_1=395~\frac{\rm W}{\rm m\cdot K}\), \(\displaystyle \lambda_2=76~\frac{\rm W}{\rm m\cdot K}\), \(\displaystyle T_1=30\;{}^\circ\)C, \(\displaystyle T_2=80\;{}^\circ\)C.
(4 pont)
solution (in Hungarian), statistics
P. 5227. \(\displaystyle a)\) Different resistors were put into two boxes. Each box contains one from each of the following resistors: 1 k\(\displaystyle \Omega\), 2 k\(\displaystyle \Omega\), 3 k\(\displaystyle \Omega\), 4 k\(\displaystyle \Omega\) and 5 k\(\displaystyle \Omega\). One resistor is taken out randomly from each box, and they are connected in series. What is the probability that the equivalent resistance of the series connection is 2 k\(\displaystyle \Omega\), 3 k\(\displaystyle \Omega\), 4 k\(\displaystyle \Omega\), 5 k\(\displaystyle \Omega\), 6 k\(\displaystyle \Omega\), 7 k\(\displaystyle \Omega\), 8 k\(\displaystyle \Omega\), 9 k\(\displaystyle \Omega\) or 10 k\(\displaystyle \Omega\)?
\(\displaystyle b)\) In other two boxes there are also some resistors. Both of these two boxes contain one from each of the following resistors: 60 k\(\displaystyle \Omega\), 30 k\(\displaystyle \Omega\), 20 k\(\displaystyle \Omega\), 15 k\(\displaystyle \Omega\) and 12 k\(\displaystyle \Omega\). One resistor is taken out randomly from each box, and they are connected in parallel. What is the probability that the equivalent resistance of the parallel connection is 30 k\(\displaystyle \Omega\), 20 k\(\displaystyle \Omega\), 15 k\(\displaystyle \Omega\), 12 k\(\displaystyle \Omega\), 10 k\(\displaystyle \Omega\), or less than 10 k\(\displaystyle \Omega\)?
(4 pont)
solution (in Hungarian), statistics
P. 5228. Calculate the distance between two lead atoms in a galena crystal, if its density and its constituents are known. (Similarly to rock salt, galena has a cubic crystal system.)
(4 pont)
solution (in Hungarian), statistics
P. 5229. Two point-like charges, each having a charge of \(\displaystyle Q\), are fixed at a distance of \(\displaystyle 2L\) from each other in weightlessness. Between these charges another point like charge of mass \(\displaystyle m\) and of charge \(\displaystyle q\) (\(\displaystyle q\) and \(\displaystyle Q\) are opposite charges) is revolving about the symmetry axis of the charges along a circular path of radius \(\displaystyle R\). The plane of this circle is the perpendicular bisector of the line segment that joins the two fixed charges.
\(\displaystyle a)\) Determine the period of the circular motion as a function of the radius of the path.
\(\displaystyle b)\) Evaluate the limiting cases when \(\displaystyle R\ll L\) and when \(\displaystyle R\gg L\).
\(\displaystyle c)\) Determine which is greater: the period of the motion of charge \(\displaystyle q\) along the circular path, or the period of the same charge when it undergoes simple harmonic motion along one of the diameters of the circle with amplitude \(\displaystyle R\)?
(Neglect the deceleration of the charge due to the radiation of the accelerating charge and due to air resistance.)
(6 pont)
Upload your solutions above.
