A KöMaL 2022. márciusi matematika feladatai

K-jelű feladatok A beküldési határidő 2022. április 11-én LEJÁRT.

---

K. 724. Juli felvágott egy pizzát egyforma szeletekre. Ezután néhány szeletet megevett, 3 szelet viszont megmaradt. Kicsit számolgatva azt vette észre, hogy az egész pizza 3/4 részét plusz egy szelet 3/4 részét ette meg. Hány szeletre vágta a pizzát?

(5 pont)

megoldás, statisztika

---

K. 725. Egy \(\displaystyle 3\times3\)-as táblázat kilenc mezőjére valamilyen sorrendben egy-egy számot írunk a következő szabály szerint: minden mezőre azt a számot írjuk, amely megmutatja, hogy annak a mezőnek hány olyan oldalszomszédja van, amire már írtunk számot. Milyen sorrendben töltöttük ki a táblázat mezőit? Hány lehetőség van? (A mezőket \(\displaystyle a1, a2, \dots, c2, c3\) kódokkal jelöljük.)

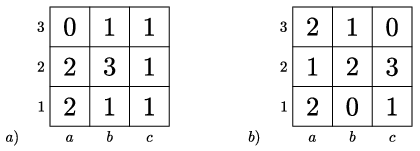
(5 pont)

megoldás, statisztika

---

K. 726. Rendezzük el az \(\displaystyle 1, 2, 3, 4, \dots, 31, 32\) számokat egy kör mentén úgy, hogy bármely két szomszédos szám összege négyzetszám legyen. Írjuk le azt is, hogy hogyan gondolkoztunk.

(5 pont)

megoldás, statisztika

K/C-jelű feladatok A beküldési határidő 2022. április 11-én LEJÁRT.

---

K/C. 727. Egy \(\displaystyle n\times n\)-es táblázat mezőire egy-egy pénzérmét helyezünk el úgy, hogy mindegyik érmén a ,,fej'' van felül. Egy lépésben bármelyik sorban vagy oszlopban pontosan három érmét fordíthatunk meg, így azokon a fejből írás lesz, az írásból pedig fej. Elérhetjük-e így valahány lépésben, hogy minden érmén írás legyen felül, ha \(\displaystyle n>2\)? Válaszunkat indokoljuk.

(5 pont)

megoldás, statisztika

---

K/C. 728. Van 10 darab számkártyánk, rajtuk az 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 számok. A számkártyákat letesszük egy sorba az asztalra és rájuk írjuk a sorszámukat, azaz 1-től 10-ig beszámozzuk a lapokat. Így minden lapon két szám szerepel. Minden lapon összeszorozzuk a két számot, majd a szorzatokat összeadjuk. Mennyi lesz a kapott érték,

\(\displaystyle a)\) ha ez a lehető legkisebb,

\(\displaystyle b)\) ha ez a lehető legnagyobb?

(5 pont)

megoldás, statisztika

C-jelű feladatok A beküldési határidő 2022. április 11-én LEJÁRT.

---

C. 1709. Az \(\displaystyle a\) és \(\displaystyle b\) egész számok osztói a 720-nak, \(\displaystyle ab\) pedig nem osztója 720-nak. Hány ilyen rendezett \(\displaystyle (a;b)\) számpár van?

Javasolta: Róka Sándor Nyíregyháza)

(5 pont)

megoldás, statisztika

---

C. 1710. Egy egységnyi oldalú négyzetbe négy kört rajzolunk az ábrán látható módon. A két nagyobbik kör egyforma méretű és érintik egymást és a négyzet oldalait is. A két kisebbik egybevágó, ezek szintén érintik a négyzet oldalait és a nagy köröket is. Mekkora a körök középpontjai által meghatározott rombusz területe?

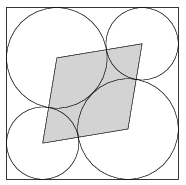
Javasolta: Gáspár Merse Előd (Budapest)

(5 pont)

megoldás, statisztika

---

C. 1711. Oldjuk meg az

\(\displaystyle \sqrt{x-1801}+\sqrt{y-1860}=2-\frac{1}{\sqrt{x-1801}} \)

egyenletet, ha \(\displaystyle x\) és \(\displaystyle y\) valós számok.

(5 pont)

megoldás, statisztika

---

C. 1712. Mekkorák lehetnek annak az ötszögnek az ismeretlen szögei, melynek minden oldala egyforma hosszúságú és van két derékszöge?

Javasolta: Károlyi Gergely (Budajenő)

(5 pont)

megoldás, statisztika

---

C. 1713. Az \(\displaystyle x\) és \(\displaystyle a\) olyan valós számok, amelyekre teljesül, hogy \(\displaystyle x+\frac{1}{x}=a\). Határozzuk meg \(\displaystyle a\) függvényében az \(\displaystyle x^{13}+\frac{1}{x^{13}}\) értékét.

(5 pont)

megoldás, statisztika

B-jelű feladatok A beküldési határidő 2022. április 11-én LEJÁRT.

---

B. 5230. Az \(\displaystyle AB\) átmérőjű félköríven kijelöltük a \(\displaystyle C\) és \(\displaystyle D\) pontokat. Az \(\displaystyle A\) és \(\displaystyle B\) pontból a \(\displaystyle CD\) egyenesre állított merőlegesek talppontját jelölje \(\displaystyle A'\), illetve \(\displaystyle B'\). Bizonyítsuk be, hogy az \(\displaystyle A'C\) és \(\displaystyle B'D\) szakaszok hossza egyenlő.

Javasolta: Surányi László (Budapest)

(3 pont)

megoldás, statisztika

---

B. 5231. Bizonyítsuk be, hogy minden \(\displaystyle n\) pozitív egészre teljesül, hogy

\(\displaystyle \sum_{k=1}^n k \cdot 2^{k-1} = \sum_{k=1}^n 2^{n-k} \cdot (2^k-1). \)

(4 pont)

megoldás, statisztika

---

B. 5232. Az \(\displaystyle ABC\) hegyesszögű háromszög belsejében, a \(\displaystyle C\)-ből induló súlyvonalon vegyük fel a \(\displaystyle P\) pontot úgy, hogy \(\displaystyle APB\sphericalangle=180^{\circ}-ACB\sphericalangle\) teljesüljön. Igazoljuk, hogy az \(\displaystyle AB\) egyenes érinti az \(\displaystyle APC\) kört.

Javasolta: Kocsis Szilveszter (Budapest)

(4 pont)

megoldás, statisztika

---

B. 5233. Egy szabályos hatszög csúcsaira véletlenszerű sorrendben felírjuk az \(\displaystyle 1, 2, \ldots, 6\) számokat. Ezután a hatszög minden oldalára ráírjuk a két végpontján szereplő számok különbségének abszolútértékét. Határozzuk meg az oldalakra írt hat szám összegének várható értékét.

Javasolta: Szoldatics József (Budapest)

(4 pont)

megoldás, statisztika

---

B. 5234. Az \(\displaystyle n\) pozitív egész számot nevezzük mitikusnak, ha minden osztója 2-vel kisebb egy prímszámnál. Például a 15 mitikus szám. Legfeljebb hány osztója lehet egy mitikus számnak? Adjuk meg az összes olyan mitikus számot, amelynek maximális számú osztója van.

Javasolta: Róka Sándor (Nyíregyháza)

(5 pont)

megoldás, statisztika

---

B. 5235. Mutassuk meg, hogy a Fibonacci-sorozatban minden \(\displaystyle 3\)-nál nagyobb prímszám \(\displaystyle 4k+1\) alakú.

(5 pont)

megoldás, statisztika

---

B. 5236. Legyen \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) három pozitív valós szám úgy, hogy \(\displaystyle abc=1\). Mutassuk meg, hogy

\(\displaystyle a+a^2+a^3 + b + b^2 + b^3 + c+ c^2 + c^3 \le {(a^2+b^2+c^2)}^2. \)

Javasolta: Lovas Márton (Budapest) és Michael Rozenberg (Izrael)

(6 pont)

megoldás, statisztika

---

B. 5237. Egy háromszögben \(\displaystyle r\) a beírt kör sugarát, \(\displaystyle R\) a köré írt kör sugarát, \(\displaystyle s\) pedig a háromszög félkerületét jelöli. Mutassuk meg, hogy ha \(\displaystyle r+2R=s\), akkor a háromszög derékszögű.

Javasolta: Fridrik Richárd Szeged)

(6 pont)

megoldás, statisztika

A-jelű feladatok A beküldési határidő 2022. április 11-én LEJÁRT.

---

A. 821. \(\displaystyle a)\) Létezik-e olyan \(\displaystyle f\colon \mathbb{N}^2\to \mathbb{N}\) függvény, melyre minden \(\displaystyle g\colon \mathbb{N}\to \mathbb{N}\) függvény és \(\displaystyle m\) pozitív egész esetén létezik \(\displaystyle n \in \mathbb{N}\), melyre a \(\displaystyle \big\{k\in \mathbb{N} \colon f(n,k)=g(k)\big\}\) halmaz elemszáma legalább \(\displaystyle m\)?

\(\displaystyle b)\) Létezik-e olyan \(\displaystyle f\colon \mathbb{N}^2\to \mathbb{N}\) függvény, melyre minden \(\displaystyle g\colon \mathbb{N}\to \mathbb{N}\) függvény esetén létezik \(\displaystyle n \in \mathbb{N}\), melyre a \(\displaystyle \big\{k\in \mathbb{N} \colon f(n,k)=g(k)\big\}\) halmaz elemszáma végtelen?

(7 pont)

megoldás, statisztika

---

A. 822. Léteznek-e \(\displaystyle p\), \(\displaystyle q\), \(\displaystyle r\) racionális számok, melyekre \(\displaystyle p+q+r=0\) és \(\displaystyle pqr=1\)?

Javasolta: Weisz Máté (Cambridge)

(7 pont)

megoldás, statisztika

---

A. 823. Legyen \(\displaystyle n\) pozitív egész, és tekintsük az \(\displaystyle S_n=\big\{(x,y,z)\colon 1\le x\le n\), \(\displaystyle 1\le y\le n\), \(\displaystyle 1\le z\le n\), \(\displaystyle x,y,z\in \mathbb{N}\big\}\) kockarácsot. Létezik-e olyan \(\displaystyle n\) pozitív egész, melyre ki lehet választani \(\displaystyle S_n\) elemei közül több, mint \(\displaystyle n\sqrt{n}\)-t úgy, hogy bármely két kiválasztott rácspont közül az egyiknek legalább két koordinátája szigorúan nagyobb legyen, mint a másik megfelelő két koordinátája?

Javasolta: Csóka Endre (Budapest)

(7 pont)

megoldás, statisztika