Fórum: A Goldbach-sejtésről

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50]

Szeretnél hozzászólni? Jelentkezz be.

[1046] bily71

2011-02-01 13:39:49

A [714]-ben azt már elismerted, hogy az f(n) az ikerprímeket számlálja.

Olvasd el figyelmesen az [1039]-beli bizonyításomat arra vonatkozólag, hogy a p(n) a 3-nál nagyobb prímeket számlálja.

Nem látom, hogy az egyenlőtlenségből az következne amit leírtál, de ha ez így van, arról nem én tehetek, hanem a prímek :D

Előzmény: [1043] Róbert Gida, 2011-02-01 13:01:18

[1045] bily71

2011-02-01 13:28:26

Dehát a d nem lehet 3! Vajon még hányszor kell itt leírnom?

A következőkben minden változó pozitív egészet jelöl, ha nem, akkor azt jelzem.

Ha 6k $\pm$ 1 számok legalább egyike összetett, akkor

6k $\pm$ 1=(6n $\pm$ n)(6m $\pm$ m),

ebből

k=6nm $\pm$ n $\pm$ m,

vagyis, ha

k $\ne$ 6nm $\pm$ n $\pm$ m,

akkor 6k-1 és 6k+1 ikerprímek.

k=6nm $\pm$ n $\pm$ m,

akkor

k=n(6m $\pm$ 1) $\pm$ m,

vagyis k tagja az ilyen alakú számokból álló számtani sorozatok egyikének.

Nyilvánvaló, hogy ha 6m $\pm$ 1 prím, akkor a d=6m $\pm$ 1 differenciához két számtani sorozat tartozik, vagyis k-ra teljesül a

k $\equiv$ $\pm$ m (mod (6m $\pm$ 1))

kongruenciák egyike.

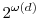Ha d=6m $\pm$ 1 összetett, akkor k szerepel az osztóihoz rendelt számtani sorozatok egyikében, amelyekből $2^{\omega(d)}$ darab van, ahol $\omega$ (d) a d osztóinak száma.

Előzmény: [1042] Maga Péter, 2011-02-01 12:47:57

[1044] Róbert Gida	2011-02-01 13:03:06
Egy másik ilyen klasszikus, nem konstans fv, de mindig prímet ad az egész helyeken: f(n)=18+(-1)ⁿ.
Előzmény: [1040] Fernando, 2011-02-01 12:22:13

[1043] Róbert Gida	2011-02-01 13:01:18
Nem is, ez az egyenlőtlenségedből következik.
Előzmény: [1041] bily71, 2011-02-01 12:24:30

[1042] Maga Péter

2011-02-01 12:47:57

Ezt a b_i-t még mindig nem értem. Mi az, hogy 'egy pozitív egész 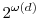$2^{\omega(d)}$ darab d differenciájú számtani sorozatban szerepelhet'?

Ha d=3, a pozitív egész pedig 2, akkor melyik az a két 3 differenciájú számtani sorozat, amiben a 2 szerepel?

Előzmény: [1034] bily71, 2011-02-01 09:59:53

[1041] bily71	2011-02-01 12:24:30
Szerintem ez nem következik a minoráns kritériumból.
Előzmény: [1038] Róbert Gida, 2011-02-01 11:28:33

[1040] Fernando	2011-02-01 12:22:13
Gidának igaza van! :)
Előzmény: [1027] Róbert Gida, 2011-01-31 23:21:37

[1039] bily71

2011-02-01 12:18:23

Igen, jól látod.

Ha véges sok ikerprím van, akkor

$\exists$ n₀ $\in$ N $\forall$ n $\in$ N n₀<n: f_n=f_n-1 $\implies$ g_n=f_n-f_n-1=0,

ebben az esetben g_n konvergens, hisz

$\forall$ n $\in$ N: g_n $\le$ g_n+1

és

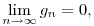
$\lim_{n\to\infty}g_n=0,$

ekkor

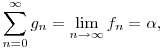
$\sum_{n=0}^{\infty}g_n=\lim_{n\to\infty}f_n=\alpha,$

ahol $\alpha$ az f_n sorozat határértéke, vagyis az ikerprímek száma.

Ha az f_n sorozat divergens, akkor a 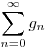$\sum_{n=0}^{\infty}g_n$ sor is divergens, vagyis ekkor az ikerprímek száma nem lehet véges.

Az [729]-beli 1. tétel bizonyítása:

Tekintsük a 6n-1 alakú számok sorozatát: 5,11,17,..., ha veszük ezen számok egyhatodának felső egészrészit, akkor a következő számsorozatot kapjuk: 1,2,3,...

Ha p|6k-1, ahol p>3 prím és p<6k-1, akkor

6k-1 $\equiv$ 0 $\implies$ k $\equiv$ (p+1)/6 (mod p),

amennyiben 6k-1 prím, úgy az előbbi kongruencia nem teljesülhet a nála kisebb p prímekre, vagyis, k nem szerepelhet a n(6m $\pm$ 1)+m alakú tagokból álló számtani sorozatok egyikében sem. Az ilyen k-k száma [p_n²/6]-ig:

$\sum_{d|P}\mu(d)\left[\frac{p_n^2+6b_1}{6d}\right].$

Itt minden d-hez csak egy számtani sorozat tartozik.

Ugyanezt az eljárást megismételhetjük a 6k+1 alakú számok esetében is (itt a számok alsó egészrészével dolgozunk), azt kapjuk, hogy a [p_n²/6]-nál nem nagyobb fenti tulajdonságú k-k száma:

$\sum_{d|P}\mu(d)\left[\frac{p_n^2+6b_2}{6d}\right],$

a két szumma összege:

$p_n=\sum_{d|P}\mu(d)\left[\frac{p_n^2+6b_1}{6d}\right]+\sum_{d|P}\mu(d)\left[\frac{p_n^2+6b_2}{6d}\right]=\sum_{d|P}\mu(d)\sum_{i=1}^2\left[\frac{p_n^2+6b_i}{6d}\right]$

kiadja a [p_n²/6]-nál nem nagyobb 3-nál nagyobb prímek számát.

Előzmény: [1037] SAMBUCA, 2011-02-01 10:45:05

[1038] Róbert Gida	2011-02-01 11:28:33
Tudod mi zavar a bizonyításodban? Az, hogy, ha igaz lenne, akkor a biz. végén levő egyenlőtlenség (egyenlőség?) szerint a prímeknek mindig a fele lenne egy ikerprímpár tagja. Ami nyilván nem igaz, még csak nagyságrendileg sem, hiszen még bizonyították is, hogy x-ig legfeljebb 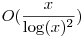$O(\frac {x}{\log (x)^2})$ ikerprím van.
Előzmény: [1025] bily71, 2011-01-31 22:41:09

[1037] SAMBUCA	2011-02-01 10:45:05
$\sum_{n=0}^{\infty}{g_n}$ miért az ikerprímek száma? Én úgy látom, hogy ennek egy részletösszege: $\sum_{n=0}^{N}{g_n} = f_N$ . Ha ez végtelenhez tart, abból mi következik? És a [729]-beli 1. tétel bizonyítását végül befejezted?
Előzmény: [1034] bily71, 2011-02-01 09:59:53

[1036] bily71	2011-02-01 10:41:41
Nem alkot, elírtam, pozitív egész számokból álló számsorozatot akartam írni.
Előzmény: [1035] SAMBUCA, 2011-02-01 10:09:10

[1035] SAMBUCA	2011-02-01 10:09:10
f(p_n²) miért alkot számtani sorozatot?
Előzmény: [1034] bily71, 2011-02-01 09:59:53

[1034] bily71

2011-02-01 09:59:53

Az f(x)-re emlékszel? x-hez azon [x/6]-nál nem nagyobb pozitív egészek számlát rendeli, melyek nem szerepelnek a (6m $\pm$ 1)n $\pm$ m alakú tagokból álló számtani sorozatok egyikében sem. Ha az f(x)-et csak az x=p_n² helyeken értelmezzük, akkor egy pozitív egészekből álló számtani sorozatot kapunk, ahol az f_n tag egyenlő a [p_n²/6]-nál nem nagyobb fenti tulajdonságú pozitív egészek számával.

A b_i tagot az alábbi összefüggésből kapjuk: a kínai maradéktétel miatt egy pozitív egész 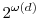$2^{\omega(d)}$ darab d differenciájú számtani sorozatban szerepelhet, melyek kezdőtagjai: 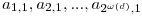$a_{1,1}, a_{2,1},...,a_{2^{\omega(d)},1}$ . Az a_i,1 kezdőtagú számtani sorozatnak p_n²-nél nem nagyobb elemeinek száma

$\left[\frac{\left[\frac{p_n^2}6\right]-a_{i,1}}d\right]+1=\left[\frac{\left[\frac{p_n^2-6a_{i,1}}6\right] }d+1\right]=\left[\frac{p_n^2-6a_{i,1}+6d}{6d}\right]=\left[\frac{p_n^2+6(d-a_{i,1})}{6d}\right],$

ebből

b_i=d-a_i,1

Az átalakításokat azért hajthattuk végre, mert az 1,6,d,a_i,1,p_n² számok egészek.

A g_n-t elírtam, helyesen:

g_n=f_n-f_n-1,

vagyis

$g_0=f_0=\left(\left[\frac{5^2}6\right]-\left[\frac{5^2-6}{6\cdot5}\right]-\left[\frac{5^2+6}{6\cdot5}\right]\right)=\left(\left[\frac{5^2}6\right]\right)-\left(\left[\frac{5^2-6}{6\cdot5}\right]+\left[\frac{5^2+6}{6\cdot5}\right]\right)$

g₁=f₁-f₀=

$\left(\left[\frac{7^2}6\right]-\left[\frac{7^2-6}{6\cdot5}\right]-\left[\frac{7^2+6}{6\cdot5}\right]-\left[\frac{7^2-6}{6\cdot7}\right]-\left[\frac{7^2+6}{6\cdot7}\right]+\left[\frac{7^2-6}{6\cdot5\cdot7}\right]+\left[\frac{7^2+6}{6\cdot5\cdot7}\right]+\left[\frac{7^2+36}{6\cdot5\cdot7}\right]+\left[\frac{7^2+174}{6\cdot5\cdot7}\right] \right)$

$-\left(\left[\frac{5^2}6\right]-\left[\frac{5^2-6}{6\cdot5}\right]-\left[\frac{5^2+6}{6\cdot5}\right]\right)=\left(\left[\frac{7^2}6\right]\right)-\left(\left[\frac{5^2}6\right]\right)-$

$-\left(\left[\frac{7^2-6}{6\cdot5}\right]+\left[\frac{7^2+6}{6\cdot5}\right]\right)+\left(\left[\frac{5^2-6}{6\cdot5}\right]+\left[\frac{5^2+6}{6\cdot5}\right]\right)+$

$+\left(\left[\frac{7^2-6}{6\cdot5\cdot7}\right]+\left[\frac{7^2+6}{6\cdot5\cdot7}\right]+\left[\frac{7^2+36}{6\cdot5\cdot7}\right]+\left[\frac{7^2+174}{6\cdot5\cdot7}\right] \right)$

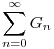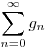A G_n sor tagjai a zárójelben lévő összegek, vagyis a $\sum_{n=0}^{\infty}G_n$ és a $\sum_{n=0}^{\infty}g_n$ sor ugyanannak a sornak az átrendezett és zárójelezett sora.

Előzmény: [1032] Maga Péter, 2011-02-01 08:29:01

[1033] bily71	2011-02-01 08:34:41
Minthogy a $\sum_{n=0}^{\infty}Q_n$ sornak az összege egyenlő a 3<p prímek számával, azért a sor divergens, következésképp nem lehet abszolút konvergens.
Előzmény: [1030] Róbert Gida, 2011-01-31 23:34:46

[1032] Maga Péter	2011-02-01 08:29:01
Nem értem... mi az f_n, mi a g_n, mi a G_n, mi a b_i?
Előzmény: [1025] bily71, 2011-01-31 22:41:09

[1031] Alma	2011-02-01 01:21:54
El nem tudjátok képzelni, vizsgára tanulás közben mennyire felüdítő tud lenni a fórum olvasgatása. Komolyan. :)

[1030] Róbert Gida	2011-01-31 23:34:46
Persze hülyeségeket írok. De, ha a sor például abszolút konvergens, akkor biztosan hamis.
Előzmény: [1029] Róbert Gida, 2011-01-31 23:32:06

[1029] Róbert Gida

2011-01-31 23:32:06

Meg is van, azt írod, hogy: $\sum_{n=0}^{\infty} Q_n=\sum_{n=0}^{\infty} |Q_n|$

ugyanakkor Q_n felváltva pozitív és negatív. Így a fenti egyenlőség biztosan hamis.

Előzmény: [1028] Róbert Gida, 2011-01-31 23:28:10

[1028] Róbert Gida

2011-01-31 23:28:10

Azért a definíciókat nem ártana visszaírnod, mert így valószínűleg csak TE érted amit leírsz.

"...vagyis az ikerprímek száma végtelen. Hol a hiba, (mert biztos van)?"

Abban biztos lehetsz.

Előzmény: [1025] bily71, 2011-01-31 22:41:09

[1027] Róbert Gida

2011-01-31 23:21:37

"Óriási dolog lenne találni egy olyan "képletet", ami minden egészre prímet adna..."

f(x)=17 ilyen, ez ráadásul nem csak az egész helyeken prím.

Előzmény: [1024] Fernando, 2011-01-31 22:28:50

[1026] Kemény Legény

2011-01-31 23:08:34

"Óriási dolog lenne találni egy olyan "képletet", ami minden egészre prímet adna..."

Nem pont az általad kért tulajdonsággal, és nem is feltétlenül konstruktív módon, de léteznek 'jó tulajdonságú képletek'.

Idézet innen:

"Legendre showed that there is no rational algebraic function which always gives primes. In 1752, Goldbach showed that no polynomial with integer coefficients can give a prime for all integer values (Nagell 1951, p. 65; Hardy and Wright 1979, pp. 18 and 22). However, there exists a polynomial in 10 variables with integer coefficients such that the set of primes equals the set of positive values of this polynomial obtained as the variables run through all nonnegative integers, although it is really a set of Diophantine equations in disguise (Ribenboim 1991). Jones, Sato, Wada, and Wiens have also found a polynomial of degree 25 in 26 variables whose positive values are exactly the prime numbers (Flannery and Flannery 2000, p. 51)."

Előzmény: [1024] Fernando, 2011-01-31 22:28:50

[1025] bily71

2011-01-31 22:41:09

"Miféle megszámolás az, amelyből még azt sem tudjuk megmondani, hogy az ilyen alakú számok x-ig vett száma korlátos-e, mint x függvénye?"

Ha az f(x)-et csak az x=p_n² helyeken vizsgáljuk, ahol p₀=5, akkor az f(n) pozitív tagú sorozatot kapjuk:

$f_0=\left[\frac{5^2}6\right]-\left[\frac{5^2-6}{6\cdot5}\right]-\left[\frac{5^2+6}{6\cdot5}\right]$

$f_1=\left[\frac{7^2}6\right]-\left[\frac{7^2-6}{6\cdot5}\right]-\left[\frac{7^2+6}{6\cdot5}\right]-\left[\frac{7^2-6}{6\cdot7}\right]-\left[\frac{7^2+6}{6\cdot7}\right]+\left[\frac{7^2-6}{6\cdot5\cdot7}\right]+\left[\frac{7^2+6}{6\cdot5\cdot7}\right]+\left[\frac{7^2+36}{6\cdot5\cdot7}\right]+\left[\frac{7^2+174}{6\cdot5\cdot7}\right]$

...

$f_n=\sum_{d|P}\mu(d)\sum_{i=1}^{2^{\omega(d)}}\left[\frac{p_n^2+6b_i}{6d}\right]$

Legyen g_n=f_n+1-f_n, ekkor a 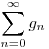$\sum_{n=0}^{\infty}{g_n}$ formális összeg egyenlő a 6k $\pm$ 1 alakú ikerprímek számával.

A következő sorozat n-edik tagja egyenlő a p_n²-nél nem nagyobb 6k $\pm$ 1 alakú prímek számával (lásd [729]-ben 1. Tétel).

$p_0=\left[\frac{5^2}6\right]-\left[\frac{5^2-6}{6\cdot5}\right]-\left[\frac{5^2+6}{6\cdot5}\right]$

$p_1=\left[\frac{7^2}6\right]-\left[\frac{7^2-6}{6\cdot5}\right]-\left[\frac{7^2+6}{6\cdot5}\right]-\left[\frac{7^2-6}{6\cdot7}\right]-\left[\frac{7^2+6}{6\cdot7}\right]+\left[\frac{7^2+36}{6\cdot5\cdot7}\right]+\left[\frac{7^2+174}{6\cdot5\cdot7}\right]$

...

$p_n=\sum_{d|P}\mu(d)\sum_{i=1}^2\left[\frac{p_n^2+6b_i}{6d}\right]$

Legyen q_n=p_n+1-p_n, ekkor 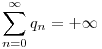$\sum_{n=0}^{\infty}q_n=+\infty$ , hiszen végtelen sok ilyen alakú prím van.

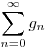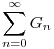A $\sum_{n=0}^{\infty}g_n$ sor tulajdonképp a $\sum_{n=0}^{\infty}G_n$ sor egy zárójelezett sora:

$G_0=\left[\frac{5^2}6\right]$ , $~G_1=-\left(\left[\frac{5^2-6}{6\cdot5}\right]+\left[\frac{5^2+6}{6\cdot5}\right]\right)$ , $~G_2=\left[\frac{7^2}6\right]$ , $~G_3=-\left[\frac{5^2}6\right]$ , $~G_4=-\left(\left[\frac{7^2-6}{6\cdot5}\right]+\left[\frac{7^2+6}{6\cdot5}\right]\right)$ , $~G_5=\left(\left[\frac{5^2-6}{6\cdot5}\right]+\left[\frac{5^2+6}{6\cdot5}\right]\right)$ , $~G_6=-\left(\left[\frac{7^2-6}{6\cdot7}\right]-\left[\frac{7^2+6}{6\cdot7}\right]\right)$ , $~G_7=\left(\left[\frac{7^2-6}{6\cdot5\cdot7}\right]+\left[\frac{7^2+6}{6\cdot5\cdot7}\right]+\left[\frac{7^2+36}{6\cdot5\cdot7}\right]+\left[\frac{7^2+174}{6\cdot5\cdot7}\right]\right)$ , $~G_8=\left[\frac{11^2}6\right]$ ,...

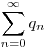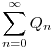Ugyanígy a $\sum_{n=0}^{\infty}q_n$ sor a $\sum_{n=0}^{\infty}Q_n$ sor egy zárójelezett sora:

$Q_0=2\left[\frac{5^2}6\right]$ , $~Q_1=-\left(\left[\frac{5^2-6}{6\cdot5}\right]+\left[\frac{5^2+6}{6\cdot5}\right]\right)$ , $~Q_2=2\left[\frac{7^2}6\right]$ , $~Q_3=-2\left[\frac{5^2}6\right]$ , $~Q_4=-\left(\left[\frac{7^2-6}{6\cdot5}\right]+\left[\frac{7^2+6}{6\cdot5}\right]\right)$ , $~Q_5=\left(\left[\frac{5^2-6}{6\cdot5}\right]+\left[\frac{5^2+6}{6\cdot5}\right]\right)$ , $~Q_6=-\left(\left[\frac{7^2-6}{6\cdot7}\right]-\left[\frac{7^2+6}{6\cdot7}\right]\right)$ , $~Q_7=\left(\left[\frac{7^2+36}{6\cdot5\cdot7}\right]+\left[\frac{7^2+174}{6\cdot5\cdot7}\right]\right)$ , $~Q_8=2\left[\frac{11^2}6\right]$ ,...

Mivel az $\omega$ (d)>0 esetekben a $\sum_{i=2}^{2}\left[\frac{p_n^2+b_i}{6d}\right]$ összeg két tagja megegyezik a $\sum_{i=1}^{2^{\omega(d)}}\left[\frac{p_n^2+b_i}{6d}\right]$ összeg két tagjával, azért a

|Q_n| $\le$ |2G_n|

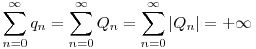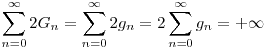
teljesül bármely n esetén. Minthogy $\sum_{n=0}^{\infty}q_n=\sum_{n=0}^{\infty}Q_n=\sum_{n=0}^{\infty}|Q_n|=+\infty$ , azért a minoráns kritérium miatt $\sum_{n=0}^{\infty}2G_n=\sum_{n=0}^{\infty}2g_n=2\sum_{n=0}^{\infty}g_n=+\infty$

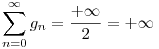Ebből $\sum_{n=0}^{\infty}g_n=\frac{+\infty}2=+\infty$ , vagyis az ikerprímek száma végtelen.

Hol a hiba, (mert biztos van)?

Előzmény: [716] Maga Péter, 2010-05-16 10:54:53

[1024] Fernando

2011-01-31 22:28:50

Valahol azért FÖLHÁBORÍTÓ, hogy ennyit nézel ki az elmúlt évszázadok matematikusaiból...

"eddigi számításaim azt igazolják,hogy százig ,,SORBAN az összes prím kiszámítható ,,vele""

Léteznek olyan polinomok is(!!), nem is nagy fokszámmal, amikkel aránylag sok prímet kaphatunk, de korántsem mindet és nem minden egész helyettesítési értékeként.

Óriási dolog lenne találni egy olyan "képletet", ami minden egészre prímet adna...

[1023] Fernando	2011-01-31 22:17:01
Szerintem Quod erat demonstrandum, de lehet, hogy tévedek. Ami fontosabb: a "bizonyításod" nem a sejtést bizonyítja. Azért érdemes belegondolni, hogy nem mai sejtésről van szó és valószínűleg "sokan" foglalkoztak már vele, nem is akármilyen matematikusok. Ami nem ugyanaz, mint múlt héten hallani róla... Nem lehetetlen esemény, hogy itt valaki egyszer csak rábukkan.
Előzmény: [1018] Jhony, 2011-01-31 20:57:59

[1022] Tóbi	2011-01-31 22:15:46
Ezek az igazi parázs szakmai viták. Visszanézek két óra múlva, és 7 hozzászólást már ki is moderáltak (gondolom nem ok nélkül). Valaki összefoglalná, mi volt? András, ne add fel! Ugyan soha nem fogjuk megérteni, min gondolkodsz, az attól még biztos jó. Végül is jártál főiskolára, meg minden.

Már regisztráltál?
Új vendég vagy?