|
| [126] bily71 | 2009-06-08 16:02:09 |
 Egyelőre elakadtam. Egyébként igazad van, a két állítás valóban ekvivalens.
Az ikerprím és a Goldbach-sejtés mélyen összefügg, nemcsak azért, mert prímekről szól mindkettő.
A táblázatot továbbra is tanulmányozni fogom. Több hasonlót is készítettem. Két dimenzióban átláthatóbbak a számok, mint egy számegyenesen.
Egyébként ez egy olyan oldal, amit matematika kedvelő emberek látogatnak. Ezeket a bizonyítási javaslatokat fogjátok fel úgy, mint érdekes matematikai feladványokat. Az, hogy nem sikerült (egyelőre), nem veszi el a kedvemet, mert nem a levezetésben volt a hiba.
|
| Előzmény: [123] Sirpi, 2009-06-08 12:23:54 |
|
| [125] Maga Péter | 2009-06-08 15:33:00 |
 Sokat járt már a szám, most végre teszek egy matematikai hozzászólást is.:)
"41+41=82
41+107=148
41+173=214
41+239=280
41+305=346=107+239
41+371=412
Ez a sor a végtelenig folytatódik, és mindig csak minden ötödik lépésnél van összetett, ami mindig öt többszöröse, ezért mindig van csere lehetőség."
Sajnos ebből csak annyi igaz, hogy ez a sor a végtelenségig folytatódik...
Az összegek második tagja 41+66k, ami nemcsak k=4,9,14,...-ra lesz összetett szám. Valóban, például k=41-re osztható 41-gyel, és 41-nél nagyobb. (Na jó, az is igaz, hogy csak minden 5. lépésben kapjuk az 5-nek többszörösét, de ettől általában még messze nem lesz prím.)
Ilyen jellegű próbálkozásokat kár tenni, mert nemkonstans egészegyütthatós polinom nem lehet minden egész helyen prím. Ha igaz lenne, amit írsz, akkor a 41+66(5n+1) ilyen polinom lenne. (Általában sem nehéz az állítás, de a konkrét esetben ellenpéldát is megadtam.) Különben is, egy elsőfokú polinom pozitív sűrűséget adna, ami teljes képtelenség.
Másrészt a Siegel-Walfisz-tétel szerint minden nemkonstans számtani sorozatban (aminek nincs triviális osztója) igaz a prímszámtétel. Ezek szerint sem lehet igaz, amit állítasz.
Harmadrészt amit állítasz, azt jelentené, hogy x-ig a prímek reciprokösszege nagyságrendileg log x, holott valójában csak log log x+O(1) (ez mondjuk lényegileg nem új az első ellenérvemhez képest:)).
|
| Előzmény: [115] bily71, 2009-06-07 18:51:34 |
|
| [124] Maga Péter | 2009-06-08 15:17:20 |
 Ez nagyon emlékeztet valamire engem. Talán egy Golomb(?) nevű matematikus annak idején (60-as évek?) éppen ezzel "valószínűsítette", hogy az ikerprím-sejtés nem igaz.
|
| Előzmény: [123] Sirpi, 2009-06-08 12:23:54 |
|
|
|
| [121] Maga Péter | 2009-06-08 00:23:40 |
 "Bocsánat, de ez a táblázat jobbra is és lefelé is végtelen, azt hittem van akkora fantáziátok, hogy ezt nem kell hozzátenni." Ahogy mondani szokás, a matematika 50% formula, 50% bizonyítás és 50% képzelőerő. Ezt persze csak a vicc kedvéért szokták ebben a sorrendben mondani, valójában a képzelőerővel kezdődik a dolog, de aztán jönnek a formulák és bizonyítások... ...lassan rátérhetnénk erre a részre is. Nekem úgy tűnik, hogy egyelőre az történt, hogy megnéztünk pár esetet, ami alapján kirajzolódott egy elképzelés (amit elmagyarázhatna végre valaki, mert én még mindig nem értem; persze lehet, hogy csak nem vagyok elég rátermett). Most az a feladat, hogy az elképzelésből állításokat csináljunk. Szóval formulák, bizonyítások...
"Vezessétek tovább a sorokat." Ezt nem lehet mondani egy bizonyítás végén. Vagyis lehet, de ez nem teszi teljessé. Vagy enélkül is bizonyítás, vagy ezzel se.
"Szerintem ez az egy sor is felülmúl minden eddigi eredményt, mert végtelen sok párost tartalmaz. Így végtelen sok párosra máris be van bizonyítva." Hát, ez azért túlzás... Mint azt valaki megjegyezte, csupán abból, hogy végtelen sok prím van, következik, hogy végtelen sok páros szám rendben van. De ennél sokkal több is ismert, az is be van bizonyítva, hogy a Goldbach-sejtés egy 0 sűrűségű halmaztól eltekintve biztosan igaz (Montgomery és Vaughan, 1975).
|
| Előzmény: [115] bily71, 2009-06-07 18:51:34 |
|
| [120] Csimby | 2009-06-08 00:08:07 |
 Triviális és sokkal jobb becslés is igaz, csak eszembe jutott, "ujjgyakorlatocska": Biz.be, hogy a Goldbach sejtésből következik, hogy a prímek száma n-ig legalább 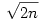 . .
|
|
|
| [118] MTM | 2009-06-07 19:56:37 |
 "Szerintem ez az egy sor is felülmúl minden eddigi eredményt, mert végtelen sok párost tartalmaz. Így végtelen sok párosra máris be van bizonyítva."
Nem értem pontosan, hogy miért múlja felül minden eddigi eredményt az, hogy bebizonyítod, hogy végtelen párosra igaz a G-sejtés. Ez triviális, hiszen veszed bármely p prímet, és p+p=2p páros, tehát végtelen sok páros felírható prímek összegére.
|
| Előzmény: [115] bily71, 2009-06-07 18:51:34 |
|
| [117] bily71 | 2009-06-07 19:01:13 |
 Ezek szerint még mindig nemtudom bebizonyítani, hogy mindig lesz két prím, ami egymással szembe kerül.
|
|
|
| [115] bily71 | 2009-06-07 18:51:34 |
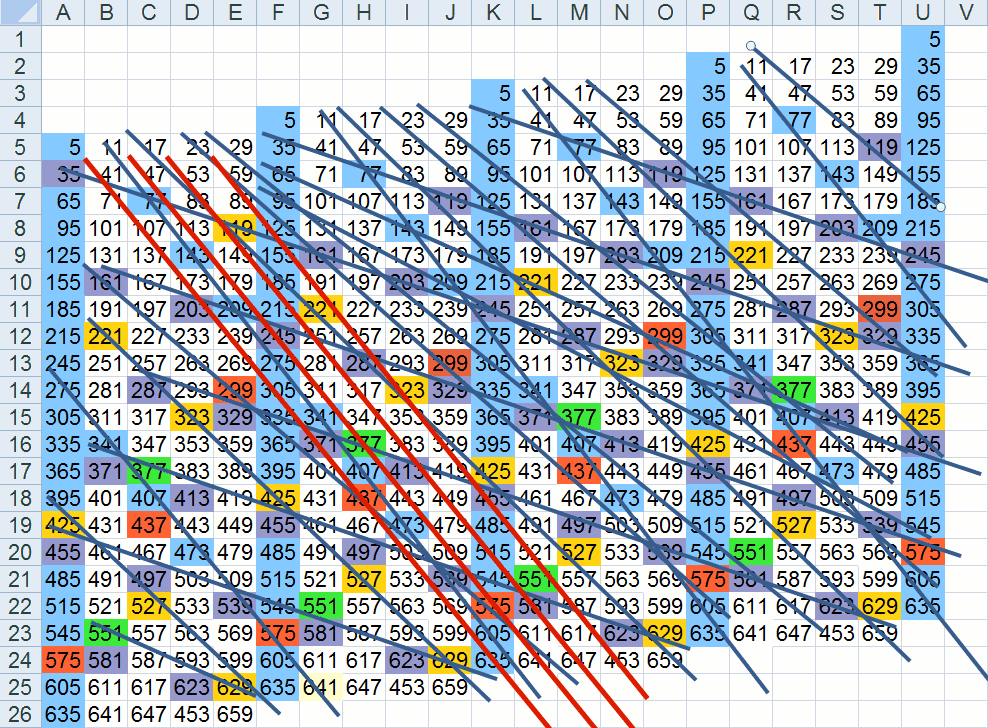
 Bocsánat, de ez a táblázat jobbra is és lefelé is végtelen, azt hittem van akkora fantáziátok, hogy ezt nem kell hozzátenni. Vezessétek tovább a sorokat.
Az egyenesek rácspontjaiban vannak az összetettek, a többi prím. A pirossal jelölt egyenesek periódikusan tartalmazzák az összetett számokat. (Több ilyen egyenes is van, végtelen sok, amit nem jelöltem.) Ezek egyik vége a végtelenbe tart. Ha ezekből csinálunk vonalzókat, a difi itt mindig 66. (egyébként minden 11 többszöröseit összekötő egyenessel párhuzamos egyenes diffije 66=6x11). Lássuk, hogy alakulnak az összegek:
41+41=82
41+107=148
41+173=214
41+239=280
41+305=346=107+239
41+371=412
Ez a sor a végtelenig folytatódik, és mindig csak minden ötödik lépésnél van összetett, ami mindig öt többszöröse, ezért mindig van csere lehetőség.
Szerintem ez az egy sor is felülmúl minden eddigi eredményt, mert végtelen sok párost tartalmaz. Így végtelen sok párosra máris be van bizonyítva. Szerintem ti is fogtok találni ilyen egyeneseket a táblázatban. Mivel végtelen sok van ilyen , minden páros fog szerepelni, ha szembefordítjuk azokat, mint vonalzókat.
|
|
| [114] Pej Nyihamér | 2009-06-07 18:47:44 |
 Ezt írtad: ,,A 41, 107, 173, 239, 305... egyenes, ami csak az 5 többszöröseit tartalmazza,azokat is szabályosan, mindig 5 lépésre, a többi prím.''
Ezzel szemben a sorozat következő két tagja, a 371=7×53 és a 437=19×23 összetett, és nem osztható 5-tel.
|
| Előzmény: [107] Sirpi, 2009-06-07 09:31:59 |
|
| [113] jonas | 2009-06-07 18:22:41 |
 Tessék, itt van az összes prímszám felsorolva, nem csak az ezer alattiak. Egyre kisebb betűvel van, úgyhogy könnyen elfér véges helyen. Ebből már látszik a tétel, nem?
|
 |
| Előzmény: [111] Maga Péter, 2009-06-07 14:52:01 |
|
|
| [111] Maga Péter | 2009-06-07 14:52:01 |
 Ez az ábra semmiképp sem bizonyítja önmagában a Goldbach-sejtést. Van ugyanis olyan páros szám, ami csak úgy írható fel két prímszám összegeként (ha egyáltalán felírható), hogy mindkét prím nagyobb, mint ezer. Az ábrán pedig nincsenek ezernél nagyobb számok.
|
| Előzmény: [108] jonas, 2009-06-07 11:34:58 |
|
| [110] Maga Péter | 2009-06-07 14:46:09 |
 Ha már mindenki érti, akkor magyarázzátok el nekem is! Egy bötűt, nem sokat, annyit sem értek ebből az egészből. Hogy készül ez az ábra?
|
|
|
|
| [107] Sirpi | 2009-06-07 09:31:59 |
 Igen, megkaptam, úgyhogy ki is rakom. A táblázatból képet csináltam, megtalálható itt. (próbáltam akkorát, hogy be tudjam ide szúrni, de túl nagy minőségromlással járt volna).
És hozzá a szöveg, amit kaptam (még korán van, hogy értelmezzem, szóval nem írok rá egyelőre semmit):
Amint láthatjuk ebben a különleges mátrixban az összetett számokra egyenesek illeszthetők. Az egyenesek torzított rácsot alkotnak. Ha pl. a 11-es szám öbbszöröseit kimetsző egyenessel párhuzamosokat húzunk, akkor ezeken az összetett számok periodikusan jelennek meg. (Végtelen sok ilyen egyenest húzhatunk, nemcsak a 11-sel párhuzamosat.) A 41, 107, 173, 239, 305... egyenes, ami csak az 5 többszöröseit tartalmazza,azokat is szabályosan, mindig 5 lépésre, a többi prím. (Itt a vonalzón 1 egység 66-ot jelent.) Ezért ha a vonalzót ezen egyenesekből alkotjuk, akkor minden további nélkül el tudjuk tolni azokat, hogy mindig biztosan találunk az N-5, N-11, N-17... számok között prímet. Ezzel a kiegészítéssel most már biztosak lehetünk abban, hogy a Goldbach- sejtés igaz.
|
| Előzmény: [105] bily71, 2009-06-07 00:25:25 |
|
| [106] bily71 | 2009-06-07 09:25:28 |
 Hasonló táblázattal, mint amit elküldtem Siprinek, az ikerprím sejtéssel kapcsolatos levezetésem azon pontja is bizonyítható, hogy minden lépésnél újabb és újabb számok maradnak ki úgy, hogy soha sehol nem bukkannak föl. Még dolgozok a megszerkesztésén, de már a fejemben összeállt a kép.
"Egy sorozat azért..." mondat tényleg hülyén hangzik, de ha jobban belegondolunk, akkor nem. A prímszámtétel például megmomdja, hogy mennyi prím van n-ig, vagy a Csebisev tétel szerint k és 2k között mindig van prím, de azt egyik ilyen tétel sem tudja megmondani, pontosan melyik lesz a prím, ezek csak statisztikai adatok. Nem a prímeket kell vizsgálni, hanem az összetetteket, ugyanis azok szabályosan követik egymást, a prímek nem.
A többszörösök valóban egy idő után átláthatatlan halmazokat alkotnak, de ez csak látszat. Úgy tűnik a diferencia és a kezdő szám helyes megválasztásával megszelidíthetők. Ha azokat a számtani sorokat állítjuk párba, amiket a Siprinek elküldött mátrixban kijelöltem, (mivel azok mindenhol szimmetrikusak), akkor mindig van olyan két prím, ami egymással szemben van. Ilyen sor végtelen sok van. Ha a mátrixba a 6n+1 alakú számokat írjuk, ugyanezeket az összefüggéseket kapjuk.
|
|
| [105] bily71 | 2009-06-07 00:25:25 |
 Sirpinek elküldöm a bizonyítás kiegészítését. Egy különleges táblázatot alkottam, amelyben olyan számtani sorozatokat tudok generálni, amiben az összetett számok periodikusan követik egymást. Ezért a vonalzót mindig el tudjuk tolni úgy, hogy pontosan ki tudjuk számolni mikor kerüljön egymással szembe két prím. Mivel végtelen sok különböző differenciájú sorozatot tudok alkotni a táblázat segítségével, minden 6k-2 alakú prímet fel tudok írni két prím összegeként. Megkérem Sirpit tegye közzé a táblázatot, hogy mindenki megismerhesse, és véleményt tudjon alkotni.
|
|
| [104] Maga Péter | 2009-06-06 23:04:20 |
 "Egy számtani sorozat pont azért sorozat, mert szabályos, és bármely jellemzője elkíséri a végtelenig."
Ez persze nem matematikai állítás, de nekem nagyon tetszik. Nagy hirtelen nem tudok rá nemtriviális ellenpéldát, és ha valamilyen matematikai formában ez igaz lenne, az egészen rendkívüli volna...
Én nem nagyon ismerem az analitikus számelméletet, de ha jól gondolom, ebből következik az, hogy nincs Siegel-gyök. Vagy: ha a Riemann-sejtés igaz, akkor az általánosított Riemann-sejtés is igaz. Ha hülyeséget beszélek, lőjetek le:)!
|
| Előzmény: [95] bily71, 2009-06-04 21:30:56 |
|
| [103] Maga Péter | 2009-06-06 22:55:36 |
 Ezeket én nem értem...:(
Szívesen megnézném a rendes levezetést én is: sajnos a kis számokon elvégzett demonstráció segítségével sem értettem meg a bizonyítások gondolatát.
Az e-mail-címem publikus.
Megjegyzés: az elején ménkű sok prím van...
|
|





 k
k