| [152] bily71 | 2009-06-10 21:15:09 |
 A lényeg az, hogy minden 2x2-es mátrix felölel egy intervallumot az x tengelyen. Minden páratlan lépésnél a páratlan sugarú körök, páros lépésnél a páros sugarú körök helyezkednek el szimmetrikusan. A többi kör csak bizonyos távolságokra lehet a fix elhelyezkedésű köröktől. Holnap készítek ábrákat, mert anélkül nehezen érthető. Lesz mindig olyan x, ahol egy kör sem metszi a számegyenest.
Remélem, nem baj, ha papíron körzővel, vonalzóval, ceruzával (úgy, mint az iskolában) szerkesztem meg, utána felszkennelem. Lehet, hogy egy kis részét értem a számelméletnek, de a matek mégiscsak a legsokoldalúbb tudomány, és ebbe beletartozik a számítógéppel való szerkesztés, vagy programozás, de én ezekből kimaradtam. És egyátalán nem tartom magam okosnak, ha sikerülne is a bizonyítás, az csak szerencse.
|
|
| [151] bily71 | 2009-06-10 10:20:31 |
 A bizonyításnál azt a tényt fogom felhasználni, hogy a sorokhoz rendelt szinuszfüggvények zérushelyei mindig meghatározott távolságra vannak egymástól. (Ahol indul a hullám, azt ne számoljuk a zérushelyek közé).
A hullámpárokat nevezzük el egyszerűen a félhullámhosszuk szerint. Így lesz 5-ös, 7-es, 11-es... hullámpárunk.
A különböző hullámpárok zérushelyei is csak bizonyos távolságokra lehetnek egymástól.
Ha az 5 többszörösei köré egységnyi sugarú köröket rajzolunk, azok a helyek, ahol a körök metszik az x tengelyt egybeesnek az 5-ös hullámpár zérushelyeivel. Azt hiszem ezt nem kell bizonyítani, ez triviális.
Minden sor a mátrixban a 6m+-1 számok többszöröseinek indexét tartalmazza. Ha az x tengelyen a 6m+-1 többszörösei köré m sugarú kört rajzolunk, azok a helyek, ahol metszik azt, egyben a sorhoz rendelt hullámpár zérushelyi is. Ezek a körök egy intervallumon belül bizonyos szimmetriákat mutatnak. Ez természetes, hiszen a zérushelyek csak meghatározott távolságokra lehetnek egymástól, így a körök, és az x tengely metszpontjai is.
Ezeket a köröket tanulmányoztam, ha eddig érthető, akkor folytatom.
|
| Előzmény: [150] Sirpi, 2009-06-09 20:13:49 |
|
|
| [149] bily71 | 2009-06-09 20:03:14 |
 Nem az a lényeg, hogy az első két sorban, attól felbukkanhat a többi sorban.
Például a 6-dik mátrixből kimarad a 37, de felbukkan a negyedik sorban, mint 13x17=37x6-1. Végtelen sok sor van függőlegesen, ezért a 2060 bárhol felbukkanhat.
Az a lényeg, hogy pl.: a 33 sehol nem szerepel, és 33x6-1=197, 33x6+1=199 ikerprímek.
Azoknak a számokat akarjuk megszámolni, amiket nem tartalmaz az egész végtelen nagy mátrix, nem csak azokat ami az első két sorban nem megtalálható.
Azt akarom bizonyítani, hogy végtelen sok ilyen szám van, és nem megnevezni akarom egyenként, mert az lehetetlen.
Az első két sorból kitudom következtetni, hogy azok közül a számok közül, amik hiányoznak az n-dik 2x2-es mátrixból, nem bukkannak föl lentebbi sorokban, persze csak az n-dik mátrixtól balra.
Ezt nem nehéz leellenőrizni az első néhány mátrixban, de az egymillárdomodiknál már egy kicsit sokáig tartana.
Most már érthető?
|
| Előzmény: [148] Pej Nyihamér, 2009-06-09 18:02:12 |
|
|
| [147] bily71 | 2009-06-09 16:00:46 |
 Természetesen azt a helyet az x tengelyen nem számítjuk a szinuszfüggvény a zérushelyeihez ahonnan indul, mert minden egész számról indítunk egy hullámot. Ha eddig érthető, akkor jelezzétek.
|
|
| [146] bily71 | 2009-06-09 15:55:10 |
 Nem az a fontos, hogy kimarad, hanem hogy ha kimarad, ne bukkanjon föl máshol. A gondolatom az, hogy ha minden 2x2-es mátrixból kimarad legalább egy szám, de egy olyan szám, ami eddig nem szerepelt a kimaradt számok között, akkor az kölcsönösen megfeleltethető az n számmal. Ugyanis az n-dik mátrixból maradt ki. Van olyan szám, hogy két mátrixból is kimarad, mert átfedik egymást az intervallumok, de az a meggyőződésem, hogy mindig van annyi szám, hogy csak az egyikhez rendeljük hozzá. Értelemszerűen a közös számokból azokat amik az előző mátrixből is kimaradtak az előzőhöz rendeljük. Mivel n a természetes számok halmazának egy eleme, és ha n minden értékéhez megfeleltethető legalább egy szám, akkor ezen számok halmazának számossága azonos lesz a természetes számok halmazának számosságával. De ha nem jól gondolom állítsatok le.
Egy példa: az 5-dik mátrixból kimarad a 30, 32, 33, 38, 40. A 25,30, 32 33 az előző 4-dik mátrixból maradt ki végleg. A 30, 32, 33 számokat az n=4, tehát a 4-dik lépéshez rendeljük, és csak a 38, 40 számokat az 5-dikhez. Ezek a számok már sehol nem bukkanak fel.(remélem).
Arra dolgoztam ki egy módszert, hogy anélkül, hogy végig böngésznénk az egész végtelen mátrixot, meg lehessen mondani biztosan, hogy sehol nem fog szerepelni. Ezt a módszert próbálom szemléletessé tenni, azért rendelek sinusfüggvényeket a számsorokhoz.
|
| Előzmény: [145] Pej Nyihamér, 2009-06-09 13:30:35 |
|
|
| [144] bily71 | 2009-06-09 13:03:28 |
 Távol áll tőlem, hogy lebecsüljem bárki tudását, főleg nem a matematika hatalmas géniuszait. Én egy senki vagyok, de jó ötletem lehet. Egyébként te is arról beszélsz, hogy új szemléletmód szükséges. Ha senki nem gondol merészet, soha nem lesz megoldva egyik probléma sem.
|
| Előzmény: [138] jenei.attila, 2009-06-09 11:00:41 |
|
| [143] bily71 | 2009-06-09 12:56:51 |
 Bocsánat! 2x2-es mátrixokról van szó.
|
|
| [142] bily71 | 2009-06-09 12:55:53 |
 A 4x4 négyes mátrixból az a szám marad ki , amit nem tartalmaz. Ezek közül lesz néhány, ami felbukkan máshol. Az első a 4-től 8-ig csak a 4, 6 és 8-at tartalmazza. A négytől nyolcig terjedő intervallum hat hosszú. (8-4)
A következő 4x4 mátrix 9-től 15-ig megint csak négy számot a 9, 11, 13, 15 számokat tartalmazza. Ez az intervallum (15-9) hat hosszú.
A következő a 14-től 22-ig terjedő intervallum, ez nyolc hosszú, négy számot, a 14, 16, 20, 22 számokat tartalmazza. És így tovább.
Tehát ezekről a 4x4-es mátrixokról beszéltem. (az ikerprímes mátrixról van szó).
A gondolatmenetem a következő. Szerkesszünk koordináta rendszert. Az x tengelyen az egység legyen pí. x egész értékei legyenek k-szor pí. (k=6mn+-n+-m.) y beosztása nem lényeges.
Indítsunk m és -m helyről szinusz hullámokat, (tehát nem az origóból), úgy hogy a félhullámhossz 6m+-1 legyen.
Az első hullámpár zérushelyei sorra: 4, 6, 9, 13... a mátrix első sora. A második hullámpár zérus helyei sorra: 6, 8, 13, 15... a mátrix második sorának felel meg, azaz n(6m+-1)+-m-nek. Itt a fél hullámhossz 5pí és 7pí.
Ha m=2 megint indul két hullámpár, az egyik 11pí, a másik 13pí fél hullámhosszal. Itt is a zérushelyek megfeleltethetők a 3-dik és a 4-dik sorral.
Bármely +-m értéknél indíthatunk szinusz hullámokat, a mátrix azon számokat tartalmazza, ahol bármely hullámnak zérus helye van. Folytatom.
|
|
| [141] Sirpi | 2009-06-09 12:34:53 |
 Ezt mondjuk jó lenne tisztázni. Bár több jel utal arra, hogy 2x2-es mátrixokra gondol (pl.: elég az 5-tel és a 7-tel foglalkozni, vagy a bal felső mátrixban a legnagyobb elem a 8).
|
| Előzmény: [140] Pej Nyihamér, 2009-06-09 12:03:02 |
|
|
|
| [138] jenei.attila | 2009-06-09 11:00:41 |
 Kedves Bily! Becsülöm a lelkesedésedet és kitartásodat, de most mintha egy kicsit szerénytelen kijelentésre ragadtattad volna magadat. Szerintem gondold át még egyszer! Nehogy a félműveltek magabiztosságának hibáját vedd magadra. Már az is elég nagy bátorságra vall, hogy ennek a két évszázados problémának ekkora önbizalommal, mondhatni naívan álltál hozzá. Sok zseniális matematikus próbálta már bevetni ellenük a modern kori matematika nehéz fegyverzetét, eddig nem teljes sikerrel. Valószínűleg valami eddig ismeretlen új módszer, vagy alapvető szemléletmód (ld. Bólyai geometria) váltás fogja megoldani a problémát. Komolyan gondolod, hogy ezek után jössz Te, és egyszerű elemi eszközökkel néhány soros frappáns megoldást adsz ezekre a problémákra? Háát.. az önbizalmadért irigyellek. Ne haragudj, nem megbántani akartalak, és semmiképp nem szeretném kedvedet szegni. Csak egy kicsit nagyobb alázatot kéne tanúsítanod.
|
| Előzmény: [137] bily71, 2009-06-09 10:16:41 |
|
| [137] bily71 | 2009-06-09 10:16:41 |
 Igaz, hogy nem tanultam, de az analízist teljesen értem, sőt a Galois elmélettől kezdve a komplex függvénytanig mindent, ami csak kapcsolatos a számelmélettel, halmazelmélettel, filozófiai hátterével stb., csak én nem képletekben gondolkozom. Mivel minden szabály valaminek az ismétlődését jelenti, ha megpróbáljuk ábrázolni bármely módszerrel (geometriai ábrák, függvények koordináta rendszerekben történő ábrázolása, prím spirál stb.), mindig valamilyen mintázatot kapunk, lásd fraktálok. Ezért próbálom felfedezni ezeket a rejtett mintázatokat. A képletekből már mindent kihoztak, amit csak tudtak, újak kellenek. Még ma ismertetek egy javaslatot a faktorizáció felgyorsítására, amit az ikerprímes mátrixból következtettem ki. (lehet, hogy már ismert).
|
| Előzmény: [133] Maga Péter, 2009-06-08 23:32:04 |
|
|
| [135] bily71 | 2009-06-09 09:51:16 |
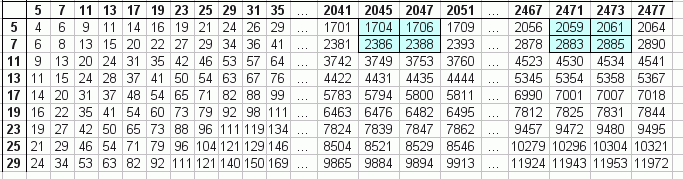
 Az ikerprímsejtéssel kapcsolatban érdekes dolgokat fedeztem fel. A végtelen mátrix első sora az 5n+-1 számokat tartalmazza, a második 7n+-1, alakúakat. A következő sor 11n+-2, 13n+-2... Minden sor így fog alakulni: n(6m+-1)+m. n a vízszintes index, m a függőleges.
Osszuk fel a végtelen mátrixot 4x4-es négyzetekre, és vizsgáljuk, hogy alakul az első két sor. (az 5n+-1, és a 7n+-1).
Az első ilyen mátrix 4-től 8-ig tartalmazza a számokat. Ábrázoljuk számegyenesen azokat a számokat amik 5-tel osztva 1, vagy 4, és 7-tel osztva 1 vagy 6 maradékot ad. Rajzoljunk az 5 és a 7 többszöröseit kijelölő számok köré 1 sugarú kört.
Minden szám, ahol metszeni fogja a számegyenest, a táblázatban szerepelni fog. Ahol nem metszi, azok a számok az ikrprímek indexei ebben az intervallumban. A többi 6m+-1 alakú szám többszöreseivel még nem kell számolni. Triviális, hogy 5 és 7- nél nem metszheti egyik kör sem a számegyenest. Minden újabb 4x4-es mátrix intervalluma kettővel hosszabb az előzőnél, és mindegyikben csak két újabb szám többszöröseinél kell kört rajzolni, mindig m sugárral.
BE TUDOM BIZONYÍTANI, HOGY AZ ELSŐ KÉT SORBAN MINDEN 4X4-ES MÁTRIXBÓL KIMARAD LEGALÁBB EGY SZÁM, AMINÉL EGYIK KÖR SEM FOGJA METSZENI A SZÁMEGYENEST.
Mivel végtelen ilyen mátrix van, végtelen az ikerprímek száma.
A részleteket félórán belül ismertetem. Ha kell küldök valakinek ábrát, hogy feltegye, (ha nem értenétek).
|
|
|
| [133] Maga Péter | 2009-06-08 23:32:04 |
 Egyébként az ikerprím- és Goldbach-sejtés között már fedeztek fel rokon szálakat. A bizonyításokat illetően nem tudni, mennyi közös vonás van, de tény, hogy amikor Brun a Brun-szitát kidolgozta, akkor azzal egyszerre meg lehetett becsülni x-ig az ikerprím-párok számát, és az x=p+q egyenlet (p,q prímek) megoldásszámát, sajnos mindkettőt csak felülről (de így is kiderültek egészen új dolgok).
Egyébként a Brun-szitát ajánlom mindenkinek. Bilynek különösképp, mert nem kell hozzá semmilyen analízisbéli előismeret (integrálás pláne nem), ugyanakkor nagyon trükkös, és mély, nehéz dolgok kijönnek belőle. Majd ha lesz egy kis időm, szétnézek, hátha van valami online, ahonnan jól lehet olvasni, vaktában nem ajánlgatok semmit.
|
|
|
| [131] bily71 | 2009-06-08 19:48:03 |
 Bocs, tévedtem, azt hittem, hogy végtelen sok egyfajta speciális alakban felírható számra sikerült bizonyítanom, ami tényleg előrelépés lenne.
|
| Előzmény: [118] MTM, 2009-06-07 19:56:37 |
|
| [130] bily71 | 2009-06-08 19:41:48 |
 A levezetés egyik esetben sem hibás, "csak" nem elég erős állításokat tartalmaz. Pl.: azt nem tudom egyelőre (lehet, hogy soha nem jutok el odáig) bizonyítani, hogy az ikerprímes mátrixban bármely szabály szerint egymást követő intervallumokból mindig marad ki olyan szám, ami később nem jön elő, a többi stimmel. A másikban pedig "csak" azt, hogy legalább egy helyen szembe kerülnek egymással a prímek.
Az igaz, hogy prímnek néztem egy két összetett számot, de ez csak baki. Nézzétek el nekem, én nem végeztem főiskolát, csak érettségim van. Mi még pl.: a gráfokról, vagy az integrálásról sem tanultunk. Mindent, amit tudok az alap gimis anyag fölött, magamtól sajátítottam el. Kb. két éve kezdtem a matekkal intenzíven foglalkozni. Kiolvastam jó pár könyvet, de nem vágom úgy a tételeket név szerint, mint ti. Mindig szerettem a matekot, mindig örömmel tölt el, ha rájövök magamtól valamire (vagy egyátalán megértek valamit), még ha egy semmiség is.
|
| Előzmény: [127] Maga Péter, 2009-06-08 16:11:28 |
|
| [129] bily71 | 2009-06-08 16:26:41 |
 Teljes mértékben igazad van. De egy számtani sorozat végtelen sok sorozatot foglal magába,(nemcsak számtanit). Ezek között keresek speciálisat, olyat, ahol a prímek valamilyen szabály szerint bukkanak fel. Most már látom, hogy ez nem lehet számtani.
|
| Előzmény: [125] Maga Péter, 2009-06-08 15:33:00 |
|
| [128] Maga Péter | 2009-06-08 16:15:49 |
 A kedvedet semmiképp se vegye el!:)
Nem elkedvetlenítés céljából szekírozzuk (legalábbis én, a többieket nem tudom, de hátha ők se:)) a bizonyításodat, hanem abból a célból, hogy amíg nem bizonyítás, addig ne higgye senki annak: se te, se én, se egy véletlenül idetévedő olvasó.
|
| Előzmény: [126] bily71, 2009-06-08 16:02:09 |
|






 N halmaz 0 sűrűségű, ha
N halmaz 0 sűrűségű, ha 