| [133] xviktor | 2005-01-07 23:04:24 |
 Az idei Matek OKTV II. kat. II.fordulójának feladatai:
1. Oldjuk meg a következő egyenletrendszert (x,y,z valós számok): lásd ábra, a kettesnél a kitevő lg(abszolútérték(y))-lg(z)
2. Az ABC háromszög BC oldalán van B1 és C1, AB oldalán a B2, AC oldalán a C2 pont. B1B2 párhuzamos AC-vel, C1C2 párhuzamos AB-vel. A B1B2 és C1C2 egyenesek metszéspontja D. Jelölje a BB1B2 és CC1C2 háromszögek területét TB és TC. a) Igazoljuk, hogy ha TB=TC, akkor az ABC háromszög súlypontja rajta van az AD egyenesen. b) Határozzuk meg TB/TC értékét, ha D az ABC háromszög beírt körének középpontja és AB=4, BC=5, CA=6.
3. Egy szabályos ötszög csúcsaiba egy-egy valós számot írtunk, majd az ötszög oldalaira és átlóira felírtuk a végpontoknál levő számok összegét. Bizonyítsuk be, hogy ha az utóbbi 10 számból 7 egész, akkor mindegyik egész kell legyen.
4. Okos Ottó felsorolta az n természetes szám pozitív osztóit nagyság szerinti sorrendben. Elsőként az 1-et, majd sorban egymás után, végül nyolcadikként következett az n. A hatodikként felsorolt d osztóról tudjuk, hogy 20=<d=<25. Mi lehetett n?
|
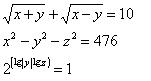 |
| Előzmény: [132] SchZol, 2005-01-07 22:39:23 |
|
|
|
| [130] SchZol | 2005-01-07 21:20:55 |
 Szia Viktor!
Tavaly 3 és fél példa kellett (24 pont), tavaly előtt viszont csak kicsit több mint 2 azt hiszem olyan 16-17pont körül volt a határ, de ebben nem vagyok biztos. Régebbi éveket nem tudom.
Üdv, Zoli
|
| Előzmény: [129] xviktor, 2005-01-07 18:24:39 |
|
| [129] xviktor | 2005-01-07 18:24:39 |
 Hi!
Egyrészt szeretném megkérdezni, hogyan sikerült a II. kategóriások OKTV-je csütörtökön, másrészt érdekelne, hogy az elmúlt évek alapján a 4-ből hány feladat kell kb. a döntőhöz.
Előre is köszi
|
|
|
| [127] Lóczi Lajos | 2004-12-20 18:09:14 |
 Persze ha ebben a formában van felírva a képlet, akkor ez így még önmagában csak "kilencedigazság", illetve "tizennyolcadigazság": hozzá kell tenni, hogy az a és b definíciójában fellépő köbgyökök lehetséges értékeit úgy kell megválasztani, hogy -3ab=p legyen, és persze a köbgyökök belsejében szereplő 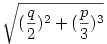 kifejezésnek mindkét előfordulásakor ugyanazt az értékét kell venni. kifejezésnek mindkét előfordulásakor ugyanazt az értékét kell venni.
|
| Előzmény: [126] SAMBUCA, 2004-12-20 00:30:27 |
|
|
| [125] Deutscher Junge | 2004-12-19 13:46:52 |
 Sziasztok!
Meg tudná írni valaki a Cardano-képletet? Segítségeteket előre is köszönöm!
|
|
|
| [123] lorantfy | 2004-12-03 12:35:56 |
 Az OKTV III. javítási útmutatója már fent van itt.
Gézának igaza van. Az 1. feladatban bal oldalon az átlók hányadosa áll.
|
|
|
| [121] KiCsa | 2004-12-02 22:21:36 |
 5. Tekintsünk egy négyoldalú gúlát, amelynek az alapja húrnégyszög. Vetítsük a gúla magasságának talppontját merőlegesen a gúla négy oldalélére. BBH a négy vetület egy körön van.
|
|
| [120] KiCsa | 2004-12-02 22:18:31 |
 4. Tekintsük a pozití vegészek olyan, k különböző elemből álló A részhalmazát, amelyre ha két (nem feltétlenül különböző) pozitív egész egyike sem eleme A-nak, akkor az összegük sincs A-ban. Maximálisan mennyi lehet A elemeinek az összege?
|
|
| [119] KiCsa | 2004-12-02 22:15:23 |
 3. Nevezzünk három, nem feltétlenül különböző, 1-nél nagyobb egészt barátságos számhármasnak, ha bármely kettő önmagánál kisebb pozitív osztóinak az összege a harmadik szám. Határozzuk meg az összes olyan barátságos számhármast, amelyben a(z egykik) legnagyobb szám páros.
|
|
| [118] KiCsa | 2004-12-02 22:11:21 |
 2. Hány 0<x<2004-re teljesül x+[x2]=x2+[x]? (Itt [c] a c valós szám (alsó) egész részét jelöli, azaz a legnagyobb olyan k egész számot, amelyre k c.) c.)
|
|
|
| [116] Maga Péter | 2004-12-02 09:18:00 |
 Este írjátok be a példákat! Meg azt is, hogy milyennek találtátok a feladatsort, illetve hogyan sikerült.
|
|
| [115] Suhanc | 2004-11-04 14:06:43 |
 Kedves SchZol!
Az megoldásod utolsó sorában szerintem szükség lenne teljes indukcióra. Illetve, talán egy olyan megjegyzés is elég, hogy az egy tag a másikká mindig ugyanúgy alakul. De lehet, hogy valami félreértek... :D
|
| Előzmény: [114] SchZol, 2004-11-04 11:37:36 |
|
| [114] SchZol | 2004-11-04 11:37:36 |
 Kedves Mihály!
Én is úgy gondolom, ahogy Te!
Egyébként meg innen már könnyű a befejezés:
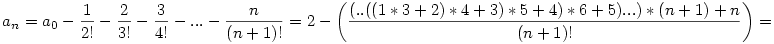
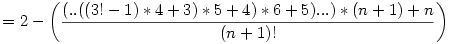
Ha a számlálót megnézünk láthatjuk, ha felbontjuk a zárójeleket, akkor rendre azt kapjuk, hogy (4!-1),(5!-1)... tehát a végén az lesz a számlálóban, hogy (n+1)!-1
Vagyis 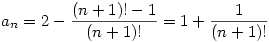
Remélem nem írtam el!
Üdv, Zoli
|
| Előzmény: [113] Fálesz Mihály, 2004-11-04 10:11:38 |
|
| [113] Fálesz Mihály | 2004-11-04 10:11:38 |
 Ha megengeditek, hogy én is hozzászóljak, szerintem a szummás alak nem sokban különbözik az eredeti definíciótól. Csupán némi átzárójelezés történt:
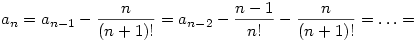
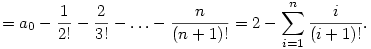
A feladat megfogalmazása tényleg nagyon szerencsétlen, de azt ki lehet találni, hogy nem arra gondoltak, hogy a rekurziót írjuk át szummára, hanem arra, hogy an-et lényegesen egyszerűbb alakban, szumma nélkül írjuk fel.
|
| Előzmény: [112] SchZol, 2004-11-03 22:20:36 |
|
| [112] SchZol | 2004-11-03 22:20:36 |
 Sziasztok!
Véleményem szerint azért nem jó a szummás alak, mert ha megkérdik a versenyzőtől, hogy mondja meg például a 8. tagot, akkor a szummás versenyző elkezdi kiszámolni a szummát tagonként, ami kb azzal ér fel, mintha egyesével kiszámolna a tagokat (a1,a2..,a8), míg aki kihozta az úgymond zárt alakot, az belehelyetít a képletbe és kész. Ez csak az Én véleményem, egyébként nem tudom mi a hivatalos álláspont!
Üdv, Zoli
|
| Előzmény: [111] Suhanc, 2004-11-03 20:50:30 |
|
| [111] Suhanc | 2004-11-03 20:50:30 |
 Kedves Fórumosok!
A verseny után a szobatársammal volt némi vitánk az első feladat kapcsán... és látva, hogy itt is élénk eszmecsere folyik, meg akartam kérdezni, arra a megoldásra, amely csak összegzi a kivonandókat, hány pontot várhatuk... de, mint kiderül, ez is max pontot ér...:)
Én is úgy érzem, nem volt egyértelmű a fogalmazás... a szobatársam példáulazzal érvelt, nem explicit alakot kértek... ez pedig, gyanús volt...
Szóval, ami egyből felmerült bennem: az explicit alak csupán az "n segítségével" kifejezés takarja, vagy eze belül műveleti megkötést is tartalmaz?
A másik: ha például egy versenyző nem is írja ki a szummázott végeredményx,t hanem elkezdei felsorolni a kvonandókat, majd ... -t rak, és odaírja az utolsó tagot, az is teljes pontszámú? Mert ez egy kicsit sántít...
Segítségeteket előre is köszönöm!
|
| Előzmény: [109] BrickTop, 2004-11-01 00:33:44 |
|
| [110] lorantfy | 2004-11-02 20:45:16 |
 Kedves Fórumosok!
Két 2000-es OKTV II. fordulós feladatot ajánlok a figyelmetekbe:
1. Egy négyzet alapú egyenes gúla alapélének és magasságának a hossza egész szám. Mekkora a gúla térfogata, ha felszínének és térfogatának azonos a mérőszáma?
2. Igazoljuk, hogy az egynél kisebb a, b, c pozitív számokra teljesül a következő egyenlőtlenség:
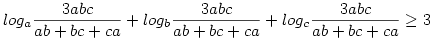
Mindkettőnek nagyon szép megoldása található az Élet és Tudomány - Sulinet Archívumban, Reiman István cikkeiben: 2000/7. és 2000/13. Keresd itt.
|
|
| [109] BrickTop | 2004-11-01 00:33:44 |
 Köszönöm az aggódást, én is szurkolok magamnak (és sorstársaimnak, mert biztosan vannak...) :) Ha ezen dőlne el a továbbjutás, elég morcos lennék. Aki továbbjutásközeli, az valószínűleg mindkétféleképpen meg tudta volna oldani az első feladatot.
Mindenesetre a tanárom nemrég értesített, már kijavította a feladatokat, és úgy tűnik maximális pontszámot kaptam a megoldásomra. Remélem, hogy hivatalos javítókulcs alapján adta meg a 7 pontot.
|
| Előzmény: [108] Maga Péter, 2004-10-31 19:12:40 |
|



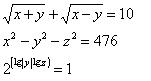






 c.)
c.)


