Fórum: Matek OKTV

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32]

Szeretnél hozzászólni? Jelentkezz be.

[48] Csizmadia Gábor	2004-01-08 21:35:56
Azért tényleg nem volt megoldhatatlan. Mindenesetre csodálkoznék, ha itt is 24 pont lenne a határ, mint az előző fordulóban...
Előzmény: [47] BrickTop, 2004-01-08 20:14:24

[47] BrickTop	2004-01-08 20:14:24
Szerintem is egyszerűek voltak, annak viszont nem fogok örülni, ha a szőrszálhasogatás dönti el, hogy ki az az 50 (vagy mennyi) ember aki a döntőbe jut.
Előzmény: [46] jenei.attila, 2004-01-08 17:57:12

[46] jenei.attila

2004-01-08 17:57:12

Sziasztok!

A Viéte formulák szerint x₁x₂+x₁x₃+x₂x₃=2p² és x₁+x₂+x₂=-2p. A második egyenletet négyzetre emelve, és kivonva belőle az első kétszeresét: x₁²+x₂²+x₃²=0. Ez pedig nem lehet három különvöző valós gyök esetén.

Szerintem a többi is nagyon egyszerű volt, és nem is kellett sokat számolni velük.

Előzmény: [43] SchZol, 2004-01-08 16:48:28

[45] SchZol

2004-01-08 16:51:17

4.feladat:

Az ABCD húrnégyszögben AB=2AD és BC=2CD; ismert továbbá az A-nál lévő $\alpha$ szög mértéke és az AC átló d hossza. Fejezzük ki a négyszög területét $\alpha$ -val és d-vel.

[44] Csizmadia Gábor

2004-01-08 16:50:15

Nos, másfél órája végetért a matek OKTV II. kategória II. fordulója. Kiváncsi vagyok nektek mi a vélemenyetek a feladatsorról. Szerintem azontúl, hogy persze nem voltak nagyon szépek a feladatok, lehet azt is mondani, hogy könnyű volt és azt is, hogy nehéz. Nehéz azért, mert hosszú, és körülményes volt megoldani a feladatokat, könnyű, mert gyakorlatilag olyanok voltak, hogy ha elkezdem, átalakítgatok, akkor kijön a megoldás.

Még nem tudom kezelni a Tex-et ezért az összes feladatot nem kísérlem meg beírni. Az Interneten mikor lesz elérhető a feladatsor és a megoldásai?

Kérdéseim: -Szerintetek mennyire volt ez nehéz példasor a korábbiakhoz képest? -Kb. hány ponton lesz meghúzva a határ? (remélem 22-23 pont elég lesz, magamat kb. ennyire saccolom)

A 3. és 4. feladatot beírom. (az első kettőben hosszú képletek vannak, amit nem tudom, hogy kell ide leírni) A hatványozást jelöltem szögletes zárójellel.

3. feladat Bizonyítsuk be, hogy nincs olyan p valós paraméter, amelyre az x[3]+2px[2]+2p[2]x+p=0 egyenletnek három különböző valós gyöke van.

(Én egyszerűen deriválással bebizonyítottam, hogy ez szig. mon. nő; remélem azért nem vonnak le pontot, mert az analízis még nincs benne a hivatalos tananyagban...)

4. feladat Az ABCD húrnégyszögben AB=2AD és BC=2CD; ismert továbbá az A-nál lévő alfa szög mértéke és az AC átló hossza. Fejezzük ki a négyszög területét alfa és d segítségével.

A helyes megoldás valószínűleg (5d[2]*sin(alfa)/8) (nem biztos!)

[43] SchZol

2004-01-08 16:48:28

3.feladat:

Bizonyítsuk be, hogy nincs olyan p valós paraméter, amelyre az x³+2px²+2p²x+p=0 egyenletnek három különböző valós gyöke van.

[42] SchZol

2004-01-08 16:46:25

2.feladat:

Az ABC háromszögben AB=c, BC=a, CA=b; a beírt kör sugara r, a köré írt köré R. Az A csúcsnál levő szög: $\alpha$ $\ge$ 90^o. Bizonyítsuk be, hogy

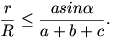
$\frac{r}{R}\le\frac{asin\alpha}{a+b+c}.$

[41] SchZol

2004-01-08 16:42:00

Ma került megrendezésre a II. kategóriás OKTV 2. fordulója. Íme a feladatok:

1. feladat:

Jelentsen n 1-nél nagyobb egész számot. Képezzük a következő két kifejezést:

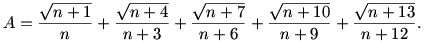
$A=\frac{\sqrt{n+1}}{n}+\frac{\sqrt{n+4}}{n+3}+\frac{\sqrt{n+7}}{n+6}+\frac{\sqrt{n+10}}{n+9}+\frac{\sqrt{n+13}}{n+12}.$

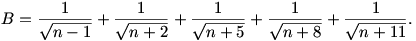
$B=\frac1{\sqrt{n-1}}+\frac1{\sqrt{n+2}}+\frac1{\sqrt{n+5}}+\frac1{\sqrt{n+8}}+\frac1{\sqrt{n+11}}.$

Döntsük el, hogy n értékétől függően az A<B, A=B, A>B kapcsolatok közül melyik állhat fenn.

[40] lorybetti

2003-12-29 14:43:01

Kedves Fórumosok!

A szünetben megnéztem a szakközépiskolások első fordulójának feladatait. Érdekes, hogy a 6. feladat bizonyítása a Helly- tételre vezethető vissza. Aki ott volt a Kömal Ankéton, az biztosan emlékszik a Helly-tételes érdekes előadásra.

A feladat a következőképp szólt:

Egy előadáson 50 személy vett részt. Tudjuk, hogy bármely négy résztvevő között van olyan, aki a másik három személy mindegyikével találkozott már korábban. Bizonyítsa be, hogy bármely négy résztvevő között van olyan személy, aki korábban már mindegyik résztvevővel találkozott!

[39] Zanaty

2003-12-25 21:49:33

Kedves Gábor!

Az OKTV II. kategória döntőben tavaly ha jól emléxem körülbelül negyvenheten voltak.

Az pedig hogy ehez hány feladatot kell megoldani (illetve hogy hány pont kell a bejutáshoz) nyílván attól függ hogy mennyire lesz nehéz a második forduló. De 3 feladat teljes megoldása szvsz elég hogy bejusson vki (4 feladat van ugyebár). Mondjuk legyegyszerűbb dolog megoldani az összes példát nem pedig rájátszani hogy 3 példa vajon elég-e ;)

Kellemes Karácsonyt mindenkinek!

[38] Csizmadia Gábor

2003-12-23 02:20:51

Most már viszont teljesen hivatalos.

Két kérdésem lenne: 1. Hányan jutnak be a II. kat. döntőjébe? 2. Kb - az előző évek tapasztalatai alapján - ehhez mekkora teljesítményt kell elérni? (3 feladat teljes megoldása elegendő?)

Köszönöm: Csizmadia Gábor

Előzmény: [33] SchZol, 2003-12-09 16:27:33

[37] Mate	2003-12-15 12:17:31
Nem

[36] bubu2	2003-12-12 17:53:54
Ha valaki megtudná mondani a III. kategória pontszámait, annak nagyon örülnék. Szerintetek elég 21 pont a továbbjutáshoz?

[35] Gábriel	2003-12-10 19:20:11
No, hát ha 24, én tökönszúrom magam:)

[34] Rácz Béla

2003-12-09 22:22:28

Hát igen, túllőttem a célon... Elnézést kérek a gőzhenger-hangnemért, de fenntartom a véleményemet, hogy nem így kéne kinéznie egy tagozatos OKTV-feladatsornak.

Lehet, hogy rosszul értelmezem az OKTV célkitűzését; ha szerepe a matematika népszerűsítése, akkor teljesen jók voltak ezek a példák. Azért vélekedem mégis másként, mert az emelt óraszámú, tehát már érdeklődő és jól felkészült versenyzőkról van szó.

Esetleg jó lenne a kitűzőknek régebbi román, bolgár vagy orosz versenyek, vagy nálunk kevésbé ismert nemzetközi versenyek, pl. a Balkáni Diákolimpiák anyagából meríteniük. A kelet-európai versenyfeladatok gyakran nemcsak nehézségben, hanem szépségben és érdekességben is megfelelnek minden igénynek. (Hadd jegyezzem meg, hogy szerintem nagyon jót tenne a mindenkori diákolimpiai csapatnak, ha részt vehetne a Balkáni Diákolimpiákon; ha jól tudom, ennek nem lenne akadálya a rendezők részéről.)

A tavalyi OKTV-döntő (III.kat.) feladataival szerintem nagyon hasonló baj volt. Úgy emlékszem, 14-en oldották meg mindhárom példát, és ráadásul nem a megoldások szépsége, érdekessége vagy általánossága alapján rangsorolták ezt a jó tucat embert, hanem a precíz, áttekinthető levezetést részesítették előnyben. Így lehetett szinte kifogástalan teljesítménnyel is kiesni a kritikus első tízből. Lehet, hogy mindez csak szubjektív vélemény (még egyszer elnézést a túlontúl kritikus hangnemért), de szerintem nem lenne baj, ha már az első fordulóban is lenne legalább egy nehezebb példa, főleg 5 órás verseny esetén. Ez persze bizonyára azt jelentené, hogy alacsonyabb pontszámmal is tovább lehetne jutni; de talán ennek is van előnye: ha valaki megoldja a nehezebb feladatot, akkor belefér, hogy egy könnyebbet elhibázzon.

A tavaly kitűzött feladatokat a friss KöMaL-ban is meg lehet nézni (461. oldal).

Előzmény: [32] Csizmadia Gábor, 2003-12-05 21:11:35

[33] SchZol

2003-12-09 16:27:33

Sziasztok!

Nem hivatalos eredmény, de állítólag 24 pont a II.kategóriában a továbbjutási ponthatár!

Üdv, Zoli

[32] Csizmadia Gábor

2003-12-05 21:11:35

Én még azt is megkockáztatnám, hogy könnyebb is volt, mint a II. kategória I. fordulója, de az biztos, hogy kevésbé macerás. Ebből a III. kategóriás feladatsorból - nem specmatos létemre - 1 óra alatt 3-at tudtam most megoldani, és így még maradna 4 órám 2 feladatra...

"Remélem, a döntőre összeszedik magukat a példagyártó fiúk, és nem a tavalyi formát hozzák."

Milyen volt tavaly a III.kat.-os döntő?

Előzmény: [31] Rácz Béla, 2003-12-05 19:15:33

[31] Rácz Béla

2003-12-05 19:15:33

Nem volt nagy színvonal. Hihetetlen, hogy ilyen pélákkal jönnek tagozatos, értelmes >=16 éves embereknek. El is ment a kedvem a példáktól, legyűrtem az utolsót és hagytam a fenébe a megjegyzéseket, meg az egyéb cuccost, hanem helyette békésen kömaloztam a megmaradó (sok) időben.

Az 1. példánál csak annyit kellett tudni, hogy általában nem igaz lg (a+b)=lg a+lg b, innen sablon. A 2. és a 3. egyszerűen kötelező tananyag specen - ez nem a memoriter-OKTV! A 4. jó példa lenne egy hatodikos Zrínyin, de azért itt... fiúk! Végül az 5., ami szinén sablon, csak egy nehézséget tartalmazott: a feladat szövegének megértését...

Ezért hát a csomó - pontatlanságért levont - nyomott töredékpont, meg esetleg az elnézett példa fog dönteni. Nem hiszem, hogy a sima 4 példa (28p) elég volna - azért csak van annyi ötpéldás, hogy ne legyen.

Remélem, a döntőre összeszedik magukat a példagyártó fiúk, és nem a tavalyi formát hozzák.

[30] Csillag

2003-12-04 21:31:26

És most már a megoldások is letölthetőek a jól ismert helyről: http://www.okszi.hu/mglds

[29] Csillag

2003-12-04 21:17:42

4. Egy földszintes elvarázsolt kastély négyzet alakú, és 2003×2003 egyforma , négyzet alakú szobára oszlik. Oldalszomszédos szobák között ajtók lehetnek. A kapubejárat az északnyugati sarokszobába vezet. A kastélyba belépve bolyongtunk egy darabig, és amikor először visszaértünk az északnyugati sarokszobába, akkor kimentünk a kastélyból. Kiderült, hogy utunk során a délkeleti (és az északnyugati) sarokszoba kivételével mindegyik szobába pontosan százszor léptünk be. Hányszor léptünk be a délkeleti sarokszobába?

5. Legyenek a₀,a₁....,a_n,a_n+1 valós számok úgy, hogy a₀=a_n+1=0. Bizonyítsuk be, hogy létezik olyan k szám, 0 $\le$ k $\le$ n, hogy (i) minden i=1,...,n-k+1-re a_k+1+...+a_k+i $\ge$ 0, és (ii) minden j=0,...,k-ra a_j+...+a_k $\le$ 0.

[28] Csillag

2003-12-04 21:13:09

Sziasztok!

Ma volt a III. kategória első fordulója. A következők voltak a feladatok:

1. Legyen a,b pozitív valós, n pozitív egész. Bizonyítsuk be, hogy

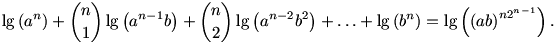
$\lg\left(a^n\right)+\binom n1\lg\left(a^{n-1}b\right)+\binom n2\lg\left(a^{n-2}b^2\right)+\dots+\lg\left(b^n\right)=\lg\left(\left(ab\right)^{n2^{n-1}}\right).$

2. Álljon a H halmaz véges sok olyan természetes számból, amelyeknek nincs 3-nál nagyobb prímosztója. Mutassuk meg, hogy a H-beli számok reciprokainak az összege 3-nál kisebb.

3. Tekintsük egy kör három pontja által meghatározott három diszjunkt körívet. Mindegyik ív felezőpontja körül megrajzoljuk a végpontjain áthaladó kört. Bizonyítsuk be, hogy a kapott három kör egy ponton halad át.

[27] Mate	2003-12-01 12:10:43
Én nem nagyon tudom elhinni, hogy a központi javítók tényleg pontosan átnézik a beküldött dolgozatokat. Szerintem csak rápillantanak a dolgozatokra, megnézik a ráírt pontszámot, és félreteszik. Pontot úgysem fognak adni, maximum levonnak, ha a tanár túl gyengekezű volt. Nekem 26 pont, remélem bemák...

[26] Gábriel

2003-11-28 16:42:01

Üdv!

Ha valaki megtudja a ponthatárt, kérem jelezze! Amúgy nekem is 23. Úgy látszik nagyon menő ez a szám.

[25] hBandi	2003-11-22 02:57:57
nekem 23 pontom lett de úgy érzem kicsit szigorúan bántak el velem 1-2 helyen, és esetleg a központi javítóktól cseppenhet +1-2 pont. jó lenne továbbjutni.

[24] BrickTop	2003-11-17 22:54:28
Még az OKTV előtt csináltam 1-2 Google-keresést és úgy tűnt 23-27 pont volt az utóbbi pár évben a határ.
Előzmény: [19] lorybetti, 2003-11-14 18:58:41

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32]

Már regisztráltál?
Új vendég vagy?