Fórum: Matek OKTV

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32]

Szeretnél hozzászólni? Jelentkezz be.

[660] Róbert Gida	2011-01-10 11:36:19
II. kategóriások nem tanulják?
Előzmény: [659] vogel, 2011-01-10 08:59:07

[659] vogel	2011-01-10 08:59:07
Nem vagy tisztában a magyar oktatással.
Előzmény: [658] Róbert Gida, 2011-01-10 01:52:38

[658] Róbert Gida	2011-01-10 01:52:38
Kínai maradéktétel semmit sem mond neked?
Előzmény: [656] Füge, 2011-01-08 13:33:35

[657] SAMBUCA	2011-01-08 14:35:17
én úgy csináltam, hogy: a 3-as és 6-os maradék mindig vagy 3-mal tér el egymástól, vagy egyenlő. Így ha mindkettő 1,2 v 3, akkor szükségképpen egyenlőek. Hasonlóan egyenlő a 4-es és 8-as maradék is. Tehát az 5-ös és 7-es is. Innen pedig nem nehéz.
Előzmény: [656] Füge, 2011-01-08 13:33:35

[656] Füge

2011-01-08 13:33:35

A tipp helyes. 3 4 6 maradékaival ki lehet zárni azt az esetet amikor 3-mal való osztásnak 2 a maradéka, illetve azt, hogy 3-mal való osztásnak 1, 4-gyel való osztásnak 1 vagy 2. Ekkor tudjuk, hogy 3-mal 1 4-gyel 3 a maradék. Ebből látszik, hogy S páratlan, ekkor 6-tal is 1 maradékot ad. Ha 4-gyel 3 a maradék akkor 8-cal 3 vagy 7, de ugye 7 nem lehet. Ekkor 5-tel és 7-tel 2 a maradék, mert az maradt. Az utolsó mondat miatt felirható, hogy S=35k+2 vagy átalakitva S=2032+35l

Innen megnézed melyik legkisebb l értékre lesz a maradék 6-tal osztva 1(ebből következik a 3-mal való osztás is), 8-cal osztva 3(ebből következik a 4-gyel való osztás is). Ez l=9, tehát S=2347

[655] SAMBUCA	2011-01-08 12:52:56
tipp: 2347
Előzmény: [654] Bärnkopf Pál, 2011-01-08 12:39:27

[654] Bärnkopf Pál	2011-01-08 12:39:27
Mennyi az S?

[653] rizsesz

2011-01-07 13:45:08

Kivételesen egyetértek Róbert Gidával... Ezek a feladatok röhejesek... És nem kell visszamenni 1960-ig matematikai tudást igénylő OKTV második fordulós feladatokhoz...

Nálunk pl. a 2005 áprilisi B. 3820 volt konkrétan az egyik feladat a második fordulóban; hadd ne mondjam, hogy mennyire nem az a szisztematikusan megoldható feladat, mint az idei második fordulósok.

Ahogy lentebb valaki írja: nem csoda, hogy 20 embernek megvolt legalább 3 egy körzetből... Bár nem értem, hogy miért nem 4...

Előzmény: [652] Róbert Gida, 2011-01-07 13:06:36

[652] Róbert Gida

2011-01-07 13:06:36

Ez logikailag biztosan rossz általánosan egy szorzatra: 12*27 példája muatatja, ez négyzetszám, egyik tag sem négyzetszám, de a kisebbik nem is osztója a nagyobbiknak.

Mondjuk egy gondolkodás nélküli befejezése a feladatnak: m⁴+17*m²+16 ez viszont két (nem szomszédos) négyzetszám közé esik: (m²)² és (m²+9)², csak 8 esetet kell végignézni, rögzített k=1,...,8-ra m⁴+17*m²+16=(m²+k)² ami egy másodfokú egyenletet jelent m-re.

1960-as években egyetemi felvételi feladatként simán kaphattátok volna ezt a feladatot, ma már ez nem követelmény.

Előzmény: [647] patba, 2011-01-06 19:48:59

[651] Nánási József	2011-01-06 21:45:16
nah... azt még csak csak megvizsgáltam, hogy y-nal párhuzamos nem lehet, de a konstans függvényt nem..., szóval nálam y=4 egyenes kimaradt.
Előzmény: [643] patba, 2011-01-06 19:38:03

[650] Vivida	2011-01-06 20:39:55
Tavalyi Arany Danira busszal mentem, elakadtam a dugóban, elkéstem, hozzá sem tudtam szólni semmihez és még előbb el is kellett mennem, hogy odaérjek Keszthelyre, a Helikonra. Ez a mostani verseny tényleg felüdülés volt :)
Előzmény: [648] patba, 2011-01-06 19:55:31

[649] Füge	2011-01-06 20:10:23
Még mindig jobb, mintha a /2-vel maradnál le:) Abban reménykedem, hogy a másik 3 feladatomba nem tudnak belekötni. Akkor még lehet esélyem :)
Előzmény: [648] patba, 2011-01-06 19:55:31

[648] patba	2011-01-06 19:55:31
ezen a másfél soron fog múlni nekem vagy 3 pont, meg lehet, hogy a döntő. mindenesetre a tavalyi arany dani döntő után(ahol első díjat nem osztottak ki, abban a kategóriában voltam) felüdülés volt ez a feladatsor.
Előzmény: [647] patba, 2011-01-06 19:48:59

[647] patba

2011-01-06 19:48:59

én úgy próbáltam, hogy átalakítottam 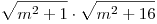$\sqrt{m^2+1} \cdot \sqrt{m^2+16}$ ha m nemnulla egész akkor a szorzat eleje biztosan irracionális. Így ha egészet akarunk, akkor a szorzat második fele az első felének a négyzetszámszorosa kell, hogy legyen. Itt ha m>2 akkor már a vége kevesebb, mint háromszorosa, de ugyanannyi sosem lesz, tehát csak a 0;+2;-2 a megoldás. Ezt persze ott nem sikerült rendesen leírni.

De Pitagoraszi számhármasokkal is ki lehet elvileg ügyeskedni valahogyan.

Előzmény: [645] Vivida, 2011-01-06 19:40:36

[646] Füge

2011-01-06 19:47:19

Legyen m⁴+17m²+16=n² Ebből m²=a helyettesítéssel

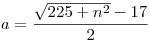
$a=\frac{\sqrt{225+n^2}-17}2$

Ennek vizsgáltam mikor lesz egész, azaz 225+n²=k²

225=k²-n²

A szomszédos négyzetszámok különbsége számtani sorozatot alkot:

b1=1 d=2

Ebből két négyzetszám különbségét úgy kapod meg, ha a b_i elemtől kezdve összeadod az elemeket b_j azaz

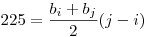
$225=\frac{b_i+b_j}2(j-i)$

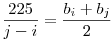
$\frac{225}{j-i}=\frac{b_i+b_j}2$

Jobb oldal egész -> bal oldal egész (j-i)|225

ugye j-i=k-n ebből kitudod számolni n-t amit visszahelyettesítesz

Picit túlbonyolítottam de más korrekt biz nem jutott eszembe.

[645] Vivida	2011-01-06 19:40:36
Nekem is az jött ki, de a megoldásokat, hogy egész legyen nem tudtam rendesen kihozni. Leírtam, hogy 0 vagy pluszminusz 2 a meredekség, de nem indokoltam meg, hogy miért csak ezek.
Előzmény: [643] patba, 2011-01-06 19:38:03

[644] Vivida	2011-01-06 19:38:21
Egyébként az a gáz, hogy lehet, hogy csak Zalában vagyunk ekkora zsenik, de itt a kb. 20 embernek mindnek legalább 3 teljes megoldása van.
Előzmény: [639] Vivida, 2011-01-06 19:21:43

[643] patba

2011-01-06 19:38:03

egyeneseket kellett felírni én úgy emlékszem.

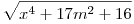$\sqrt{x^4+17m^2+16}$ lett a két pont távolsága(nekem ez jött ki). Ebből kellett volna meghatározni a lehetséges megoldásokat, de nem lett meg, csak egy.( +/- 2 kimaradt)

Szerintem sem volt túlzottan nehéz, de mégis lett két hibám(a másik a 3. feladat végén volt, azt meg tudtam határozni, hogy melyik maradék melyikhez tartozik, de aztán valahogy sikerült kizárni a jó megoldást, és egy nagyobb számot találtam így, nem a legkisebbet.). Épp ezért nem hiszem, hogy ez döntő lesz nekem...

Előzmény: [640] Füge, 2011-01-06 19:28:24

[642] Füge	2011-01-06 19:37:42
Akkor a jó feladatom örülök, ha 3 pontos lesz:) Sebaj a többi elvileg jó.. Remélem elég lesz:)

[641] Vivida	2011-01-06 19:34:17
"Határozzuk meg az összes olyan egész meredekségű egyenest", én ezt úgy értettem, hogy egyenlettel adjuk meg, de ezen biztos semmi nem fog múlni. Ha mégis, akkor hűdenagyon peches vagy...
Előzmény: [640] Füge, 2011-01-06 19:28:24

[640] Füge	2011-01-06 19:28:24
Én elírtam benne egy részt és a végén $\frac{25-17}2=8$ lett, szal az m= $\pm$ 2 megoldásokat elvesztettem :-/ Nem tudod véletlenül fel kellett írni az egyeneseket vagy csak a meredekség volt kérdés? Mert azokat se írtam fel:)
Előzmény: [639] Vivida, 2011-01-06 19:21:43

[639] Vivida	2011-01-06 19:21:43
Szerintem sem volt vészes, bár a második feladatom nem lett tökéletes.
Előzmény: [638] Füge, 2011-01-06 18:20:30

[638] Füge

2011-01-06 18:20:30

Ma volt a Matek OKTV II. kat II. forduló. Kinek hogy ment? Szerintem nem volt vészes.

1. Egy tetraéder éleire valós számokat írunk úgy, hogy a kitérő éleken lévő számok összege ugyanannyi legyen. A csúcsokhoz odaírjuk a 3 befutó élre írt számok összegét, ezek legyenek a,b,c,d. Továbbá igaz, hogy a=b=2c=2d. Igazoljuk, hogy van olyan él, amelyre a 0 szám került.

2. Adott egy y=x² egyenletű parabola és egy P(0;4) pont. Határozzuk meg az összes olyan egész meredekségű egyenest, amely átmegy a P ponton és a parabola belsejébe eső szakasz hossza is egész.

3. Melyik az a legkisebb S>2010 egész szám, amelyet a 3,4,5,6,7,8 számokkal elosztva az pontosan kétszer kapjuk az 1,2,3 maradékokat.

4. Igazoljuk, hogy akkor és csak akkor téglalap a t területű ABCD konvex négyszög, ha

4t=(AB+CD)(AD+BC)

[637] Erben Péter

2010-12-06 18:16:23

Matematika OKTV, III. kategória, 2010-2011-es tanév, első forduló

1. Egy 2010×2010-es táblázat mezőibe úgy akarunk (nem feltétlenül különböző) egész számokat beírni, hogy minden sorban és minden oszlopban a számok összege különböző legyen (azaz 4020 különböző összeget kapjunk). Legkevesebb hányféle szám beírásával tudjuk ezt elérni?

2. Legyen 0<x₁<x₂<...<x_n<1. Igazolja, hogy

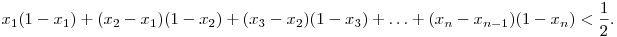
$x_1(1-x_1)+(x_2-x_1)(1-x_2)+(x_3-x_2)(1-x_3)+\dots +(x_n-x_{n-1})(1-x_n)<\frac 12.$

3. Keresse meg az összes olyan p prímszámot, melyhez léteznek olyan a,b,c egész számok, hogy a²+b²+c²=p és 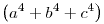$\left(a^4+b^4+c^4\right)$ osztható p-vel.

4. Egy n-elemű H halmaznak kiválasztottuk néhány k-elemű részhalmazát (3 $\le$ k $\le$ n) úgy, hogy H bármely két elemét pontosan három darab, bármely három elemét pontosan két darab kiválasztott részhalmaz tartalmazza. Határozza meg n és k lehetséges értékeit.

5. (a) Tükrözzük az ABC háromszög A csúcsát B-re, B-t C-re, C-t A-ra. Igaz-e, hogy ha a tükörképek alkotta háromszög szabályos, akkor az eredeti háromszög is szabályos?

(b) Tükrözzük az ABCD tetraéder A csúcsát B-re, B-t C-re, C-t D-re, D-t A-ra. Igaz-e, hogy ha a tükörképek alkotta tetraéder szabályos, akkor az eredeti tetraéder is szabályos?

[636] Füge

2010-12-03 20:46:15

Felkerült az OH honlapjára a Matek OKTV I-II. kat feladatsor/javítókulcs.

http://oh.gov.hu/3-2-2-aktualis-verseny/oktv/oktv-2010-2011-elso-fordulo

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32]

Már regisztráltál?
Új vendég vagy?