|
| [669] Füge | 2011-02-08 15:15:50 |
 Azt elfelejtettem írni, hogy II. kategóriában természetesen :)
|
|
| [668] Füge | 2011-02-08 15:05:50 |
 Az idei ponthatár 24 pont.
|
|
|
|
| [665] Füge | 2011-01-10 19:54:19 |
 Köszönöm. Régebbi hozzászólásban olvastam, azért kérdeztem meg.
|
|
|
| [663] Füge | 2011-01-10 14:34:56 |
 Sziasztok.
Egy olyan kérdésem lenne, hogy még mindig él az a lehetőség, hogy ha az OKTV döntőn valamilyen eredményt elérsz, akkor 100%-os emelt érettségit kapsz? És ha igen akkor matekon mi ez a határ? Valamint ha februárban jelentkezem emelt érettségire, és esetleg elérem ezt a bizonyos eredményt OKTV-n (márciusban), akkor attól még el kell mennem érettségizni?
Előre is köszönöm. Üdv Füge
|
|
|
| [661] D. Tamás | 2011-01-10 13:45:18 |
 Kínai maradéktételt? Sajnos még a közelébe se érünk. Elvileg semmilyen komoly és komolytalan egyenlőtlenséget nem fogok tanulni középiskolában. (Csebisev-, Cauchy–Bunyakovszkij–Schwarz)-, Nesbitt-, Jensen- stb. sőt mi több sem a rendezési tételt és még mindettől függetlenül komplexeket sem tanítanak, vagy ha igen akkor nagyon alacsony szinten.) Nevetséges ami a közoktatásban folyik (kivétel a spec. matekosoknak), ezt 11. évfolyamosként tapasztalom. Egy kicsit fárasztó hogy sok-sok héten át tanulunk analitikus geometriát de olyan szinten hogy az már egyszerűen nevetséges. Majdnemhogy még 'gondolkodni' sem kell. A többiről meg ne is beszéljünk...
|
|
|
|
|
| [657] SAMBUCA | 2011-01-08 14:35:17 |
 én úgy csináltam, hogy: a 3-as és 6-os maradék mindig vagy 3-mal tér el egymástól, vagy egyenlő. Így ha mindkettő 1,2 v 3, akkor szükségképpen egyenlőek. Hasonlóan egyenlő a 4-es és 8-as maradék is. Tehát az 5-ös és 7-es is. Innen pedig nem nehéz.
|
| Előzmény: [656] Füge, 2011-01-08 13:33:35 |
|
| [656] Füge | 2011-01-08 13:33:35 |
 A tipp helyes. 3 4 6 maradékaival ki lehet zárni azt az esetet amikor 3-mal való osztásnak 2 a maradéka, illetve azt, hogy 3-mal való osztásnak 1, 4-gyel való osztásnak 1 vagy 2. Ekkor tudjuk, hogy 3-mal 1 4-gyel 3 a maradék. Ebből látszik, hogy S páratlan, ekkor 6-tal is 1 maradékot ad. Ha 4-gyel 3 a maradék akkor 8-cal 3 vagy 7, de ugye 7 nem lehet. Ekkor 5-tel és 7-tel 2 a maradék, mert az maradt. Az utolsó mondat miatt felirható, hogy S=35k+2 vagy átalakitva S=2032+35l
Innen megnézed melyik legkisebb l értékre lesz a maradék 6-tal osztva 1(ebből következik a 3-mal való osztás is), 8-cal osztva 3(ebből következik a 4-gyel való osztás is). Ez l=9, tehát S=2347
|
|
|
|
| [653] rizsesz | 2011-01-07 13:45:08 |
 Kivételesen egyetértek Róbert Gidával... Ezek a feladatok röhejesek... És nem kell visszamenni 1960-ig matematikai tudást igénylő OKTV második fordulós feladatokhoz...
Nálunk pl. a 2005 áprilisi B. 3820 volt konkrétan az egyik feladat a második fordulóban; hadd ne mondjam, hogy mennyire nem az a szisztematikusan megoldható feladat, mint az idei második fordulósok.
Ahogy lentebb valaki írja: nem csoda, hogy 20 embernek megvolt legalább 3 egy körzetből... Bár nem értem, hogy miért nem 4...
|
| Előzmény: [652] Róbert Gida, 2011-01-07 13:06:36 |
|
| [652] Róbert Gida | 2011-01-07 13:06:36 |
 Ez logikailag biztosan rossz általánosan egy szorzatra: 12*27 példája muatatja, ez négyzetszám, egyik tag sem négyzetszám, de a kisebbik nem is osztója a nagyobbiknak.
Mondjuk egy gondolkodás nélküli befejezése a feladatnak: m4+17*m2+16 ez viszont két (nem szomszédos) négyzetszám közé esik: (m2)2 és (m2+9)2, csak 8 esetet kell végignézni, rögzített k=1,...,8-ra m4+17*m2+16=(m2+k)2 ami egy másodfokú egyenletet jelent m-re.
1960-as években egyetemi felvételi feladatként simán kaphattátok volna ezt a feladatot, ma már ez nem követelmény.
|
| Előzmény: [647] patba, 2011-01-06 19:48:59 |
|
|
| [650] Vivida | 2011-01-06 20:39:55 |
 Tavalyi Arany Danira busszal mentem, elakadtam a dugóban, elkéstem, hozzá sem tudtam szólni semmihez és még előbb el is kellett mennem, hogy odaérjek Keszthelyre, a Helikonra. Ez a mostani verseny tényleg felüdülés volt :)
|
| Előzmény: [648] patba, 2011-01-06 19:55:31 |
|
| [649] Füge | 2011-01-06 20:10:23 |
 Még mindig jobb, mintha a /2-vel maradnál le:) Abban reménykedem, hogy a másik 3 feladatomba nem tudnak belekötni. Akkor még lehet esélyem :)
|
| Előzmény: [648] patba, 2011-01-06 19:55:31 |
|
| [648] patba | 2011-01-06 19:55:31 |
 ezen a másfél soron fog múlni nekem vagy 3 pont, meg lehet, hogy a döntő. mindenesetre a tavalyi arany dani döntő után(ahol első díjat nem osztottak ki, abban a kategóriában voltam) felüdülés volt ez a feladatsor.
|
| Előzmény: [647] patba, 2011-01-06 19:48:59 |
|
| [647] patba | 2011-01-06 19:48:59 |
 én úgy próbáltam, hogy átalakítottam 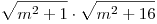 ha m nemnulla egész akkor a szorzat eleje biztosan irracionális. Így ha egészet akarunk, akkor a szorzat második fele az első felének a négyzetszámszorosa kell, hogy legyen. Itt ha m>2 akkor már a vége kevesebb, mint háromszorosa, de ugyanannyi sosem lesz, tehát csak a 0;+2;-2 a megoldás. Ezt persze ott nem sikerült rendesen leírni. ha m nemnulla egész akkor a szorzat eleje biztosan irracionális. Így ha egészet akarunk, akkor a szorzat második fele az első felének a négyzetszámszorosa kell, hogy legyen. Itt ha m>2 akkor már a vége kevesebb, mint háromszorosa, de ugyanannyi sosem lesz, tehát csak a 0;+2;-2 a megoldás. Ezt persze ott nem sikerült rendesen leírni.
De Pitagoraszi számhármasokkal is ki lehet elvileg ügyeskedni valahogyan.
|
| Előzmény: [645] Vivida, 2011-01-06 19:40:36 |
|
| [646] Füge | 2011-01-06 19:47:19 |
 Legyen m4+17m2+16=n2 Ebből m2=a helyettesítéssel
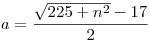
Ennek vizsgáltam mikor lesz egész, azaz 225+n2=k2
225=k2-n2
A szomszédos négyzetszámok különbsége számtani sorozatot alkot:
b1=1 d=2
Ebből két négyzetszám különbségét úgy kapod meg, ha a bi elemtől kezdve összeadod az elemeket bj azaz
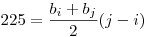
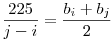
Jobb oldal egész -> bal oldal egész (j-i)|225
ugye j-i=k-n ebből kitudod számolni n-t amit visszahelyettesítesz
Picit túlbonyolítottam de más korrekt biz nem jutott eszembe.
|
|





