Fórum: Matek OKTV

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32]

Szeretnél hozzászólni? Jelentkezz be.

[680] Maga Péter	2011-07-26 09:28:25
Igen. Én is így csináltam anno. Egyébként a 2002-es első válogatón volt, ha jól emlékszem, az első feladat. Ott xy-1 és x-y álltak xy+1 és x+y helyett. Továbbá nem a legnagyobbat kellett megtalálni, hanem az összeset. Pontosan a 24 osztói jók. (A legnagyobb a 24.)
Előzmény: [679] Kemény Legény, 2011-07-26 08:48:19

[679] Kemény Legény

2011-07-26 08:48:19

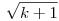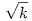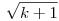Az akkori megoldásom mellesleg nem volt túl kreatív, a Csimby által elkezdett úton vázlatosan: $\forall$ (k,p)=1 $\implies$ p² $\equiv$ 1(k), azaz pl. minden 1<p<k prímre p|k vagy k $\le$ p²-1. Tehát a $\sqrt{k+1}$ -nél kisebb (prím)számok mind osztói a k-nak. 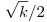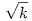Az pedig egyrészt ismert, hogy mik ezek a számok ( $\sqrt{k}$ -val $\sqrt{k+1}$ helyett megtalálható a Skljarszkij-Csencov-Jaglom:...-ban), másrészről egy egyszerű becsléssel kijön, hogy 'túl sok' prím van, azaz ha k elég nagy, akkor a Csebisev-tétel miatt van prím $\sqrt{k}/2$ és $\sqrt{k}$ között, ill. 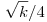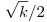$\sqrt{k}/4$ és $\sqrt{k}/2$ között ill. 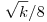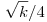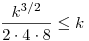$\sqrt{k}/8$ és $\sqrt{k}/4$ között, ezek szorzatából pedig adódik egy felső becslés k-ra: $\frac{k^{3/2}}{2\cdot 4 \cdot 8}\le k$ . Lényegében tehát csak véges sok k-t kell megvizsgálni, de további egyszerű ötletekkel ez jelentősen csökkenthető (pl. p=2,3 bevételével sokat javul a becslés, egészen addig, hogy versenyen is gyorsan le lehessen ellenőrizni, még úgy is, hogy emlékeim szerint nekünk az összes k-t meg kellett határozni a válogatón...)

[678] Kemény Legény	2011-07-26 08:16:19
Érdekes ez a feladat, főleg azért, mert 2004-ben érettségiztem, mégis tisztán emlékszem, hogy korábban már ezt a feladatot (vagy ezzel teljesen ekvivalenset) megoldottam egy versenyen. Nevezetesen egy 2003-2004 körüli olimpiai válogatóverseny 1-2. feladata lehetett, csak azokat nem találom sehol a neten... Lehetséges, hogy alig 1-2 éven belül 2 versenyen is feladták volna ugyanazt??
Előzmény: [675] Csimby, 2011-07-25 23:02:03

[677] Csimby	2011-07-26 08:07:59
Igazad van, csomó helyen hibás lépéseket csinálok mert gyűrűben vagyunk, nem testben. Köszi hogy szóltál, ha már úgyis megoldottad érdekelne a megoldásod.
Előzmény: [676] Róbert Gida, 2011-07-26 01:50:26

[676] Róbert Gida	2011-07-26 01:50:26
Nincs igazad, k=8-ra például 4 inkongruens megoldás van. De a befejezést sem látom, hogy akkor mi lett k=6-tal, az teljesíti a feltételeket vagy sem (bár tökmindegy mert ahogy látom k=8 teljesíti a feltételeket és 8>6). Egyébként k=24 a megoldás. Azért valami minimális pontot biztos adnának a megoldásodra.
Előzmény: [675] Csimby, 2011-07-25 23:02:03

[675] Csimby

2011-07-25 23:02:03

2004-2005 III. kat döntő 2. feladat (ennek a fordulónak nem találom a megoldásait sem a kormányoldalon, se máshol)

Határozzuk meg a legnagyobb olyan k egészt, amely rendelkezik az alábbi tulajdonsággal: Minden olyan esetben, amikor az x, y egész számokra xy+1 osztható k-val, akkor x+y is osztható k-val.

Tegyük fel, hogy k rendelkezik a tulajdonsággal. Minden x mod k redukált maradékosztályhoz egyértelműen létezik a -x^-1 mod k redukált maradékosztály, melyre x(-x^-1)+1 $\equiv$ 0 (mod k) és így a tulajdonság miatt x-x^-1 $\equiv$ 0 (mod k) vagyis x² $\equiv$ 1 (mod k) teljesül minden x mod k redukált maradékosztályra. Ennek az egyenletnek maximum kettő (k>2-re pontosan kettő) megoldása van: x $\equiv$ $\pm$ 1 (mod k). Azt kaptuk tehát, hogy a mod k redukált maradékosztályok száma legfeljebb 2. Nem nehéz belátni, hogy k=6 a legnagyobb egész melyre $\varphi$ (k) $\le$ 2.

Előzmény: [193] KiCsa, 2005-03-03 19:27:18

[674] logarlécész	2011-03-04 17:34:35
Valaki megírná a második kategóriás döntő példáit? Előre is köszönöm!

[673] Maga Péter	2011-03-02 18:02:44
Nem rossz példák, a 2. és a 3. kifejezetten érdekesek (mint kérdések), azt gondolom. Mindazonáltal egyiket sem találom kifejezetten nehéznek: a 2. és a 3. esetében az első ötletem jó volt, az 1.-höz sajnos nem volt ötletem, de az meg közvetlenül számolható, nem is bonyolult (gondolom, ügyes geométer arra is megtalálja a szép megoldást).
Előzmény: [672] Erben Péter, 2011-03-01 19:42:47

[672] Erben Péter

2011-03-01 19:42:47

2010-2011, III. kategória, döntő

1. Az ABC derékszögű háromszög C csúcsából induló magasságának talppontja az AB átfogón D. A B csúcsból induló szögfelező a CD magasságot az E, az AC befogót az F pontban metszi. Igazoljuk, hogy AD>2^.EF.

2. Van-e olyan pozitív egész, amelynek pozitív osztói között 2011-szer annyi négyzetszám van, mint köbszám?

3. Anna és Bálint a következő játékot játsszák: Anna rajzol egy tetszőlegesen nagy üres (azaz él nélküli) gráfot, majd egyesével behúz tetszőleges éleket, amelyeket Bálint közvetlenül a behúzás után kékre vagy pirosra színez. További szabály, hogy az így keletkező gráfban minden csúcs foka legfeljebb k lehet, és k értékében előre megállapodnak. Melyik az a legkisebb k, amely mellett Anna ügyes játékkal mindenképpen létre tud hozni egy 2011 hosszúságú egyszínű utat?

[671] Füge	2011-02-08 16:39:20
Mert eddig akárhányszor írtam ide, mindig a II. kategóriáról volt szó.

[670] Róbert Gida	2011-02-08 16:31:49
Mitől lenne természetes, honnan tudnám?
Előzmény: [669] Füge, 2011-02-08 15:15:50

[669] Füge	2011-02-08 15:15:50
Azt elfelejtettem írni, hogy II. kategóriában természetesen :)

[668] Füge	2011-02-08 15:05:50
Az idei ponthatár 24 pont.

[667] Alma	2011-01-10 21:44:14
Szerintem 2008-ban is. Talán az volt az utolsó.
Előzmény: [666] vogel, 2011-01-10 20:11:07

[666] vogel	2011-01-10 20:11:07
Szerintem 2007-ben még adtak. Mennyi az a régóta?
Előzmény: [664] Róbert Gida, 2011-01-10 16:47:32

[665] Füge	2011-01-10 19:54:19
Köszönöm. Régebbi hozzászólásban olvastam, azért kérdeztem meg.

[664] Róbert Gida	2011-01-10 16:47:32
OKTV helyezésér már régóta nem adnak érettségit.
Előzmény: [663] Füge, 2011-01-10 14:34:56

[663] Füge

2011-01-10 14:34:56

Sziasztok.

Egy olyan kérdésem lenne, hogy még mindig él az a lehetőség, hogy ha az OKTV döntőn valamilyen eredményt elérsz, akkor 100%-os emelt érettségit kapsz? És ha igen akkor matekon mi ez a határ? Valamint ha februárban jelentkezem emelt érettségire, és esetleg elérem ezt a bizonyos eredményt OKTV-n (márciusban), akkor attól még el kell mennem érettségizni?

Előre is köszönöm. Üdv Füge

[662] vogel	2011-01-10 14:34:20
Én vidéki III. kategóriásként max. lineáris kongruenciáról hallottam.
Előzmény: [660] Róbert Gida, 2011-01-10 11:36:19

[661] D. Tamás

2011-01-10 13:45:18

Kínai maradéktételt? Sajnos még a közelébe se érünk. Elvileg semmilyen komoly és komolytalan egyenlőtlenséget nem fogok tanulni középiskolában. (Csebisev-, Cauchy–Bunyakovszkij–Schwarz)-, Nesbitt-, Jensen- stb. sőt mi több sem a rendezési tételt és még mindettől függetlenül komplexeket sem tanítanak, vagy ha igen akkor nagyon alacsony szinten.) Nevetséges ami a közoktatásban folyik (kivétel a spec. matekosoknak), ezt 11. évfolyamosként tapasztalom. Egy kicsit fárasztó hogy sok-sok héten át tanulunk analitikus geometriát de olyan szinten hogy az már egyszerűen nevetséges. Majdnemhogy még 'gondolkodni' sem kell. A többiről meg ne is beszéljünk...

[660] Róbert Gida	2011-01-10 11:36:19
II. kategóriások nem tanulják?
Előzmény: [659] vogel, 2011-01-10 08:59:07

[659] vogel	2011-01-10 08:59:07
Nem vagy tisztában a magyar oktatással.
Előzmény: [658] Róbert Gida, 2011-01-10 01:52:38

[658] Róbert Gida	2011-01-10 01:52:38
Kínai maradéktétel semmit sem mond neked?
Előzmény: [656] Füge, 2011-01-08 13:33:35

[657] SAMBUCA	2011-01-08 14:35:17
én úgy csináltam, hogy: a 3-as és 6-os maradék mindig vagy 3-mal tér el egymástól, vagy egyenlő. Így ha mindkettő 1,2 v 3, akkor szükségképpen egyenlőek. Hasonlóan egyenlő a 4-es és 8-as maradék is. Tehát az 5-ös és 7-es is. Innen pedig nem nehéz.
Előzmény: [656] Füge, 2011-01-08 13:33:35

[656] Füge

2011-01-08 13:33:35

A tipp helyes. 3 4 6 maradékaival ki lehet zárni azt az esetet amikor 3-mal való osztásnak 2 a maradéka, illetve azt, hogy 3-mal való osztásnak 1, 4-gyel való osztásnak 1 vagy 2. Ekkor tudjuk, hogy 3-mal 1 4-gyel 3 a maradék. Ebből látszik, hogy S páratlan, ekkor 6-tal is 1 maradékot ad. Ha 4-gyel 3 a maradék akkor 8-cal 3 vagy 7, de ugye 7 nem lehet. Ekkor 5-tel és 7-tel 2 a maradék, mert az maradt. Az utolsó mondat miatt felirható, hogy S=35k+2 vagy átalakitva S=2032+35l

Innen megnézed melyik legkisebb l értékre lesz a maradék 6-tal osztva 1(ebből következik a 3-mal való osztás is), 8-cal osztva 3(ebből következik a 4-gyel való osztás is). Ez l=9, tehát S=2347

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32]

Már regisztráltál?
Új vendég vagy?