|
| [697] Antal János Benjamin | 2012-01-07 15:51:10 |
 Én elnéztem egy napot, és pénteken akartam menni OKTV-re, elég idegesítő volt a dolog. Pedig úgy keltem fel pénteken, hogy bennem volt az, hogy bejutok a harmadik fordulóba. Szívesen megpróbálnám megoldani a feladatokat, ha valaki leírná őket( II. kategória). Most a programozás és info OKTV-re hajtok, azokon is bejutottam a második fordulóba, hátha az egyiken elcsípek egy harmadik fordulót :)
|
|
| [696] D. Tamás | 2012-01-06 21:41:43 |
 Tavaly 24 pontnál húzták meg, ha jól rémlik, bár picit soknak tartom azt a 300-at. Csak a Komárom-Esztergom megyéből 8-an voltunk, abból 1 valaki I. kategóriás továbbjutó volt.
Hát ezek után szerintem jobb, ha nem is reménykedem.
|
| Előzmény: [695] Bärnkopf Pál, 2012-01-06 21:34:48 |
|
| [695] Bärnkopf Pál | 2012-01-06 21:34:48 |
 Azt hiszem, 300-an jutottak a második fordulóba (a verseny kiírás alapján), de azt nem lehet tudni, hogy megyénként ez mennyit jelent. Erről nem mondanak semmit, és szerintem statisztikák sem készülnek róla.
A behívás pedig szerintem elég necces. Én idén sem hiszem, hogy behívnak, pedig szerintem részletesen leírtam a megoldásokat, amik (egyenlőre úgy tűnik) jók is. Összesen max. 50 ember jut a döntőbe.
Tavaly is csaknem hibátlan volt, amit írtam de lehúzták annyira hogy pont nem jutottam tovább. Lehet, hogy a többi dolgozat (azoké, akik tovább jutottak) tényleg jobb volt - ezt elismerem, de hogy a végső pontszámom nem volt reális, az biztos.
Úgyhogy reménykedni mindig lehet, én is bízom a továbbjutásban, de nem nagyon hiszek benne.
|
| Előzmény: [694] D. Tamás, 2012-01-06 20:00:54 |
|
| [694] D. Tamás | 2012-01-06 20:00:54 |
 Ezek a jó megoldások -szerintem is -, elsőben utólag nekem is ez jött ki, a többi meg teljesen megegyezik.
Remélem valahogy a végére még beférek a behívottak közé, bár egyre inkább úgy érzem hogy erre nincs sok esély.
Tényleg, lehet tudni hogy mennyien jutottunk egyáltalán a II. fordulóba? Szívesen megnézném, mondjuk megyékre leosztva.
|
| Előzmény: [693] Bärnkopf Pál, 2012-01-06 18:48:43 |
|
| [693] Bärnkopf Pál | 2012-01-06 18:48:43 |
 Szerintem is könnyű volt (ha nem írtam rosszakat, azaz nem értettem valamit nagyon félre). Egyesek szerint könnyebb volt, mint az első forduló.
1.: 1925
2.: (2pí;pí), (pí;2pí), (-pí;-2pí), (-2pí;pí)
3.: "Csak" be kellett látni (több (szerintem) jó elvileg különböző megoldást is hallottam.)
4.: (2;2)
Én ezeket írtam, persze vagy jók, vagy nem. (Remélem inkább az első.) :-)
Az a baj, hogy a leíráson még nagyon sok múlik, ha a megoldás jó is, mert valószínűleg sok ember lesz hibátlan közelében.
Ha nem lett jó, az azért bosszantó, mert 12:08-ra kész voltam, és rengetegszer átnéztem. Persze saját hibát nehezen vesz észre az ember, főleg, ha benne van a gondolatmenetben.
|
| Előzmény: [692] D. Tamás, 2012-01-05 15:57:06 |
|
| [692] D. Tamás | 2012-01-05 15:57:06 |
 Kinek hogy ment a mai matek OKTV? (II. kategória)
Szerintem nem volt nehéz, bár én hoztam a "formámat" és a legegyszerűbb feladatot (1-es) naná hogy elrontottam. Kb. addig jó hogy beláttam hogy kettővel és hárommal sem osztható. Remélem van/lesz itt olyan is, aki szintén ugyanezt írta.
|
|
| [691] Róbert Gida | 2011-10-17 20:21:45 |
 Lehet, hogy emiatt vannak könnyű feladatok:
http://nol.hu/belfold/20110930-nem_honoraljak_a_tetelsorirast
Ilyen esetben szerintem az lenne a megoldás, hogy hagyják a francba a tételírást a tanárok és adják fel mindig az előző év feladatait.
|
| Előzmény: [689] R.R King, 2011-10-17 18:01:50 |
|
|
| [689] R.R King | 2011-10-17 18:01:50 |
 Igen, valóban könnyű volt, 3 feladat akár simán benne lehetne az emelt érettségiben is. Mindezek ellenére szerintem messze nem ez lesz az országos átlag amit leírtál. A szakközepes kategóriában voltak ezeknél nehezebb feladatok is, ami meglepő, hiszen ott elvileg gyengébb a mezőny..
|
| Előzmény: [688] logarlécész, 2011-10-17 17:18:53 |
|
| [688] logarlécész | 2011-10-17 17:18:53 |
 Szerintem azért nincs szó az OKTV-ről, mert annyira könnyű volt, hogy nincs mit beszélni róla (a második kategóriáról beszélek).
Legfeljebb az ötös feladatról érdemes szót ejteni, bár ott is elég hamar valószínűnek tűnt, hogy a bizonyítás nem fog menni, tehát érdemes ellenpéldát keresni.
Nekem 35 pont lett. Az egyik feladatra (3.) adtam második (elvileg különböző) megoldást, de arra sajnos nem adnak pluszpontot. Egyébként ezzel nem vagyok egyedül az iskolában, hárman írtunk max-pontosat. És a csoportomból (15 fő) 10 ember továbbküldhetőt írt.
Úgyhogy nézzük az I. vagy a III. kategóriát, mert a II.-at nem érdemes.
|
| Előzmény: [687] R.R King, 2011-10-17 15:38:07 |
|
| [687] R.R King | 2011-10-17 15:38:07 |
 Sziasztok!
Szokatlanul nagy a csend az első fordulóról. Ki milyennek találta idén a sort? (Bármelyik kategóriában)
|
|
|
|
| [684] Róbert Gida | 2011-07-26 10:55:35 |
 Legyen k olyan mely rendelkezik a tulajdonsággal. Tegyük fel, hogy k-nak van 3-nál nagyobb prímosztója, legyen egy ilyen p, és pa az n pontos prímhatványosztója. Ekkor az x 2mod pa, 2mod pa,
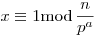 kongurenciarendszer kínai miatt megoldható, a megoldás relatív prím n-hez, mert p>2. Továbbá x2 kongurenciarendszer kínai miatt megoldható, a megoldás relatív prím n-hez, mert p>2. Továbbá x2 4mod p, de x2 4mod p, de x2 1mod n is igaz, így x2 1mod n is igaz, így x2 1mod p is, ellentmondás (p>3 volt). Így csak 2,3 lehet az n prímosztója, de akkor x=5 relatív prím n-hez, így 52 1mod p is, ellentmondás (p>3 volt). Így csak 2,3 lehet az n prímosztója, de akkor x=5 relatív prím n-hez, így 52 1mod n, azaz n|24 és a legnagyobb közülük n=24 jó is. 1mod n, azaz n|24 és a legnagyobb közülük n=24 jó is.
|
| Előzmény: [677] Csimby, 2011-07-26 08:07:59 |
|
| [683] R.R King | 2011-07-26 09:47:57 |
 Üdv.
Én az alábbi feladathoz kérnék segítséget. Ez is egy régi Oktv feladat volt: x,y pozitív egész p prímszám, oldjuk meg az alábbi egyenletet: x3-y2=4p Ehhez így nincs túl sok ötletem... (Egy netes oldalon találtam, könnyen megeshet, hogy elírás és y kitevője is 3, de úgy meg bírom oldani) Köszi a segítséget előre is.
|
|
|
| [681] Maga Péter | 2011-07-26 09:38:30 |
 Ami a kreativitást illeti: abból persze triviális, hogy hogyan néz ki egy adott modulus mellett a multiplikatív csoport. Akkor ezt még nem tudtuk, és ezért nincs ezzel a megoldással semmi baj.
|
| Előzmény: [679] Kemény Legény, 2011-07-26 08:48:19 |
|
| [680] Maga Péter | 2011-07-26 09:28:25 |
 Igen. Én is így csináltam anno. Egyébként a 2002-es első válogatón volt, ha jól emlékszem, az első feladat. Ott xy-1 és x-y álltak xy+1 és x+y helyett. Továbbá nem a legnagyobbat kellett megtalálni, hanem az összeset. Pontosan a 24 osztói jók. (A legnagyobb a 24.)
|
| Előzmény: [679] Kemény Legény, 2011-07-26 08:48:19 |
|
| [679] Kemény Legény | 2011-07-26 08:48:19 |
 Az akkori megoldásom mellesleg nem volt túl kreatív, a Csimby által elkezdett úton vázlatosan:  (k,p)=1 (k,p)=1 p2 p2 1(k), azaz pl. minden 1<p<k prímre p|k vagy k 1(k), azaz pl. minden 1<p<k prímre p|k vagy k p2-1. Tehát a p2-1. Tehát a 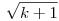 -nél kisebb (prím)számok mind osztói a k-nak. Az pedig egyrészt ismert, hogy mik ezek a számok ( -nél kisebb (prím)számok mind osztói a k-nak. Az pedig egyrészt ismert, hogy mik ezek a számok (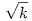 -val -val 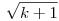 helyett megtalálható a Skljarszkij-Csencov-Jaglom:...-ban), másrészről egy egyszerű becsléssel kijön, hogy 'túl sok' prím van, azaz ha k elég nagy, akkor a Csebisev-tétel miatt van prím helyett megtalálható a Skljarszkij-Csencov-Jaglom:...-ban), másrészről egy egyszerű becsléssel kijön, hogy 'túl sok' prím van, azaz ha k elég nagy, akkor a Csebisev-tétel miatt van prím 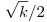 és és 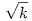 között, ill. között, ill. 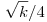 és és 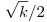 között ill. között ill. 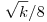 és és 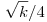 között, ezek szorzatából pedig adódik egy felső becslés k-ra: között, ezek szorzatából pedig adódik egy felső becslés k-ra: 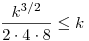 . Lényegében tehát csak véges sok k-t kell megvizsgálni, de további egyszerű ötletekkel ez jelentősen csökkenthető (pl. p=2,3 bevételével sokat javul a becslés, egészen addig, hogy versenyen is gyorsan le lehessen ellenőrizni, még úgy is, hogy emlékeim szerint nekünk az összes k-t meg kellett határozni a válogatón...) . Lényegében tehát csak véges sok k-t kell megvizsgálni, de további egyszerű ötletekkel ez jelentősen csökkenthető (pl. p=2,3 bevételével sokat javul a becslés, egészen addig, hogy versenyen is gyorsan le lehessen ellenőrizni, még úgy is, hogy emlékeim szerint nekünk az összes k-t meg kellett határozni a válogatón...)
|
|
| [678] Kemény Legény | 2011-07-26 08:16:19 |
 Érdekes ez a feladat, főleg azért, mert 2004-ben érettségiztem, mégis tisztán emlékszem, hogy korábban már ezt a feladatot (vagy ezzel teljesen ekvivalenset) megoldottam egy versenyen. Nevezetesen egy 2003-2004 körüli olimpiai válogatóverseny 1-2. feladata lehetett, csak azokat nem találom sehol a neten... Lehetséges, hogy alig 1-2 éven belül 2 versenyen is feladták volna ugyanazt??
|
| Előzmény: [675] Csimby, 2011-07-25 23:02:03 |
|
|
| [676] Róbert Gida | 2011-07-26 01:50:26 |
 Nincs igazad, k=8-ra például 4 inkongruens megoldás van. De a befejezést sem látom, hogy akkor mi lett k=6-tal, az teljesíti a feltételeket vagy sem (bár tökmindegy mert ahogy látom k=8 teljesíti a feltételeket és 8>6). Egyébként k=24 a megoldás. Azért valami minimális pontot biztos adnának a megoldásodra.
|
| Előzmény: [675] Csimby, 2011-07-25 23:02:03 |
|
| [675] Csimby | 2011-07-25 23:02:03 |
 2004-2005 III. kat döntő 2. feladat (ennek a fordulónak nem találom a megoldásait sem a kormányoldalon, se máshol)
Határozzuk meg a legnagyobb olyan k egészt, amely rendelkezik az alábbi tulajdonsággal: Minden olyan esetben, amikor az x, y egész számokra xy+1 osztható k-val, akkor x+y is osztható k-val.
Tegyük fel, hogy k rendelkezik a tulajdonsággal. Minden x mod k redukált maradékosztályhoz egyértelműen létezik a -x-1 mod k redukált maradékosztály, melyre x(-x-1)+1 0 (mod k) és így a tulajdonság miatt x-x-1 0 (mod k) és így a tulajdonság miatt x-x-1 0 (mod k) vagyis x2 0 (mod k) vagyis x2 1 (mod k) teljesül minden x mod k redukált maradékosztályra. Ennek az egyenletnek maximum kettő (k>2-re pontosan kettő) megoldása van: x 1 (mod k) teljesül minden x mod k redukált maradékosztályra. Ennek az egyenletnek maximum kettő (k>2-re pontosan kettő) megoldása van: x  1 (mod k). Azt kaptuk tehát, hogy a mod k redukált maradékosztályok száma legfeljebb 2. Nem nehéz belátni, hogy k=6 a legnagyobb egész melyre 1 (mod k). Azt kaptuk tehát, hogy a mod k redukált maradékosztályok száma legfeljebb 2. Nem nehéz belátni, hogy k=6 a legnagyobb egész melyre  (k) (k) 2. 2.
|
| Előzmény: [193] KiCsa, 2005-03-03 19:27:18 |
|
| [674] logarlécész | 2011-03-04 17:34:35 |
 Valaki megírná a második kategóriás döntő példáit? Előre is köszönöm!
|
|





 2mod pa,
2mod pa, 
 (k,p)=1
(k,p)=1 p2
p2 p2-1. Tehát a
p2-1. Tehát a  1 (mod k). Azt kaptuk tehát, hogy a mod k redukált maradékosztályok száma legfeljebb 2. Nem nehéz belátni, hogy k=6 a legnagyobb egész melyre
1 (mod k). Azt kaptuk tehát, hogy a mod k redukált maradékosztályok száma legfeljebb 2. Nem nehéz belátni, hogy k=6 a legnagyobb egész melyre  (k)
(k)